学案1
前言:找的题有点少,见谅,毕竟纯考基础算法的题也不多QwQ
upd8/17:为了凑篇幅长度,为了详细一点,加上了代码。
基础算法&思想:
普通贪心
思想:
顾名思义,贪心算法总是作出在当前看来最好的选择。也就是说贪心算法并不从整体最优考虑,它所作出的选择只是在某种意义上的局部最优选择。当然,希望贪心算法得到的最终结果也是整体最优的。虽然贪心算法不能对所有问题都得到整体最优解,但对许多问题它能产生整体最优解。如单源最短路经问题,最小生成树问题等。在一些情况下,即使贪心算法不能得到整体最优解,其最终结果却是最优解的很好近似。
简结:emmm,选择局部最优。
适用问题:整体最优性可以被局部最优性推导出。(+不知道正解的题)
证明贪心方法:
- 微扰:即任意交换相邻两项都会使整体变差
- 范围缩放:扩大局部范围选取最优,不会使整体差
- 决策包容性:就是劣解能到达的情况,优解都能到达(
优解包含劣解) - 反证法
- 数学归纳法
- 直觉:如果不是特别简单的题,会有坑,但仍然可以“凭天生的灵感直奔终点”。
由于正常贪心被讲过很多遍了,所以仅简单说一下。
例题
题目描述
CJB 知道是误会之后,跟你道了歉。你为了逗笑他,准备和他一起开始魔法。不过你的时间不多了,但是更惨的是你还需要完成 \(n\) 个魔法任务。假设你当前的时间为 \(T\),每个任务需要有一定的限制 \(t_i\) 表示只有当你的 \(T\) 严格大于 \(t_i\) 时你才能完成这个任务,完成任务并不需要消耗时间。当你完成第 \(i\) 个任务时,你的时间 \(T\) 会加上 \(b_i\),此时要保证 \(T\) 在任何时刻都大于 \(0\),那么请问你是否能完成这 \(n\) 个魔法任务,如果可以,输出 \(\texttt{+1}\texttt{s}\),如果不行,输出 \(\texttt{-1}\texttt{s}\)。
这题的话,先想出来了一个错误的贪心(按照\(b_i\)的值从大到小排序)可是会有问题。
当\(T+b_1<t_2\)然而\(T+b_2>t_1\)这时候先选择2更合适
排序顺序就出来啦,再按题意模拟一遍即可。
这题挺有意思的,思考思考。
先不管三七二十一,凑到一定能A爆对方的情况,然后再考虑多出的情况,通过玩牌经验,3攻击力的是最不优秀的,1其次,2理想。所以在凑够的时候,考虑按照312的顺序还回去就ok了。
后悔贪心
浅谈思想:
先找一个错误的贪心,然后把错误的选择改为正确的。
参考博客:
反悔堆:
P2949 用时一定的反悔贪心
先按照一般的错误贪心写,不对了再利用小根堆替换。
附上代码:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+10;
struct sss{
int val,date;
bool operator<(const sss &aaa)const{
return val>aaa.val;
}//重载成小根堆
}w[N];
priority_queue<sss> q;
bool cmp(sss x,sss y)
{
if(x.date!=y.date)return x.date<y.date;
else return x.val>y.val;
}
ll ans;
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d%d",&w[i].date,&w[i].val);
}
sort(w+1,w+n+1,cmp);
for(int i=1;i<=n;i++)
{
if(w[i].date>q.size())//可以放进去
{
ans+=w[i].val;
q.push(w[i]);
}
else //和前面有冲突,选择与堆顶比较
{
if(w[i].val>q.top().val)//较堆顶更为优秀,替换
{
ans-=q.top().val;
q.pop();
q.push(w[i]);
ans+=w[i].val;
}
//不如堆顶优秀,无视
}
}
printf("%lld",ans);
return 0;
}
P4053 价值一定的反悔贪心
这题和上面那题没啥区别甚至代码只需要该两三处,这题的“价值”就是 一个物品耗费的time ,只不过我们想要“价值”最小罢了。
附上代码:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=150050;
struct sss{
int time,date;
bool operator<(const sss &aaa)const{
return time<aaa.time;
}//重载成小根堆
}w[N];
priority_queue<sss> q;
bool cmp(sss x,sss y)
{
if(x.date!=y.date)return x.date<y.date;
else return x.time<y.time;
}
int ans;
ll last;
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d%d",&w[i].time,&w[i].date);
}
sort(w+1,w+n+1,cmp);
for(int i=1;i<=n;i++)
{
if(last+w[i].time<w[i].date)//可以放进去
{
ans++;
last+=w[i].time;
// cout<<last<<"*/*/\n";
q.push(w[i]);
}
else //和前面有冲突,选择与堆顶比较
{
if(w[i].time<q.top().time)//较堆顶更为优秀,替换
{
ans--;
last-=q.top().time;
q.pop();
q.push(w[i]);
last+=w[i].time;
ans++;
}
//不如堆顶优秀,无视
}
}
printf("%d",ans);
return 0;
}
反悔自动机:
CF865D Buy Low Sell High(堆反悔自动机)
对于这题来说,大佬的博客讲得可能太细了……
基础的贪心思想是:
对于一个点 \(i\) 往后选取一个 \(j\) ,若\(a[j]\)比\(a[i]\)大,则选取这一对,\(ans+=a[j]-a[i]\)。
很明显,当后面有一个 \(k\) 点,\(a[k]>a[j]\)时,有可能会让答案更优。
例子:
3
1 2 100
显然应该放弃2,选择卖出100。
考虑后悔:
我们用一个价值 \(val\) 的物品来帮助我们完成当前的 \(k\) 点与 \(val\) 物品配对后等价于放弃 \(j\) 选择 \(k\) 这个操作,简单推导可得\(val=a[j]\)。
语言是苍白且无力的,看代码:
for(int i=1;i<=n;i++)
{
if(!q.empty() && (q.top()<a[i]))//堆顶比当前小
{
ans+=a[i]-q.top();
q.pop();
q.push(a[i]);
}
q.push(a[i]);
}
详细代码:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=300005;
int a[N];
ll ans;
priority_queue<int ,vector<int>,greater<int> >q;
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
for(int i=1;i<=n;i++)
{
if(!q.empty() && (q.top()<a[i]))//堆顶比当前小
{
ans+=a[i]-q.top();
q.pop();
q.push(a[i]);
}
q.push(a[i]);
}
printf("%lld",ans);
return 0;
}
P3620 [APIO/CTSC2007] 数据备份(双向链表反悔自动机)
这个题挺好玩的。
题意:
首先把题目化成为选取k个点,每个点选取后与之相邻都不可被选,最后希望和最小。
错误的贪心想法:
每次选最小的。
Hack例子:
2 1 2 9
事实证明选1不如选2 2优。
考虑后悔
题解讲得挺好还有图看它吧。

这道题就没了。
不,还有附上代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+10;
const int INf=0x3f3f3f3f;
int nxt[N];
int pre[N];
int vis[N];
int dis[N];
int a[N];
struct sss{
int val,pos;
sss(int _val=0,int _pos=0)
{
val=_val;
pos=_pos;
}
bool operator <(sss aaa) const
{
return val>aaa.val;
}
};
priority_queue<sss> q;
void change(int x)
{
vis[pre[x]]=vis[nxt[x]]=true;
pre[x]=pre[pre[x]];//手玩一下
nxt[x]=nxt[nxt[x]];
nxt[pre[x]]=x;
pre[nxt[x]]=x;
}
signed main()
{
int n,k;
scanf("%lld%lld",&n,&k);
for(int i=1;i<=n;i++)
{
scanf("%lld",&a[i]);
}
for(int i=1;i<n;i++)
{
nxt[i]=i-1;
pre[i]=i+1;
dis[i]=a[i+1]-a[i];
q.push(sss(dis[i],i));
}
dis[0]=dis[n]=INf;
int ans=0;
for(int i=1;i<=k;i++)
{
while(vis[q.top().pos])//被删过
{
q.pop();
}
sss now=q.top();
q.pop();//取出当前最优解,并将其标记删除
int id=now.pos;
ans+=dis[id];
dis[id]=dis[nxt[id]]+dis[pre[id]]-dis[id];
q.push(sss(dis[id],id));
change(id);
}
printf("%lld",ans);
return 0;
}
分治
分治,把一个复杂的问题分成多个简单问题,直接求解,最后合并。这个思想是很多高效算法的基础,例如排序算法(快速排序,归并排序),傅里叶变换(快速傅里叶变换)等,但这里不讲。
可以用分治需要满足的性质:
- 该问题的规模缩小到一定的程度就可以容易的解决。
- 该问题具有最优子结构性质。
- 利用该问题分解出的子问题的解可以合并为该问题的解。
- 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
大概的流程可以分为三步:分解 -> 解决 -> 合并。
- 分解原问题为结构相同的子问题。
- 分解到某个容易求解的边界之后,进行递归求解。
- 将子问题的解合并成原问题的解。
Tips:思想是没有上限的。
可以使用分治法求解的一些经典问题:
- 二分搜索
- 大整数乘法
- Strassen矩阵乘法
- 棋盘覆盖
- 合并排序
- 快速排序
- 线性时间选择
- 最接近点对问题
- 循环赛日程表
- 汉诺塔
考虑到某些原因,就不细讲了。
放一道好玩的题:
希望不出锅。
P6406 Norma
该题题意很简洁,求\(\Sigma len*min*max\).
思路类似CDQ分治,给定一个区间\([L,R]\)将其划分为\([L,mid]\)和\([mid+1,R]\)求解跨过\(mid\)的区间的贡献后,再递归计算\([L,mid]\)和\([mid+1,R]\)。
考虑固定一个点i,使其范围在\([L,mid]\)中,求出右区间对它的贡献,最后所有\(i \in[L,mid]\)相加求和。
上面只是大题思路,下面细讲一下如何求右边对\(i\)的贡献。
细想一下,题目求\(\Sigma len*min*max\).我们可以从\(min\)和\(max\)入手,先处理出左边区间的最小值和最大值,记为\(minn\)和\(maxx\)再处理出\(minn\)和\(maxx\)在右边能维持的最大范围。下标分别记做\(j,k\)。
于是乎,有了\(j,k\)两点后,右边被分成了三部分。
为了便于表示,设两点中靠左的点为\(x\),靠右的点为\(y\)。
第一部分:\([mid+1,x]\)
对于这一部分来说,最小值和最大值是前文提到的\(minn\)和\(maxx\),是固定的所以可以\(O(1)\)求解。
第二部分:\([x+1,y]\)
由于\(j\)和\(k\)的相对位置的不同会导致不一样的情况,所以需要分类讨论。为了方便,下面仅举\(j<k\)的例子:
\(j<K\)时,意味着区间最小值不是\(minn\),而区间最大值仍然是\(maxx\),那就考虑如何求解右边的区间最小值的贡献。
为了方便,设当前在右边的指针为\(F\),当前的最小值为\(mi\)
朴素想法求贡献:
如果真按照它这样求,那计算不用想都知道是不优秀的。
接下来我们对它来稍微改一下后,再运用乘法分配律:
这样我们就可以用两个前缀和来优化啦。
我们可以用前缀和来分成两段处理。
用前缀和分成两段而不能合为一的原因在于式子中有个i,
明显如果不分开这个i的话,就是个暴力了,
所以考虑分开i。
我们使用两个前缀和数组,
其中一个表示 右端点到 mid+1 的 minnlen 和,
由于我们还需要 i 到 mid 的 lenminn 和,
我们就需要另一个前缀和数组 存的是 minn 和(它(i-mid+1) 就是我写的乘法分配律的那个式子 )
两个前缀和相加maxx(第二个前缀和需要乘(i-mid+1))就是第二段对 i 的贡献。
后言:讲课的时候可能会在黑板上画图,所以就不贴图片啦
附上代码:
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10;
const int P=1e9;
const int INf=INT_MAX;
#define ll long long
ll a[N];
ll ans;
ll s1[2][N];
ll s2[2][N];
ll s3[2][N];
ll Gaosi(int a,int b)
{
return (a+b)*(b-a+1)/2;
}
void Estar(int L,int R)
{
if(L==R)
{
(ans+=a[L]*a[L]%P)%=P;
return;
}
if(L+1==R)
{
(ans+=(a[L]*a[L]%P+a[R]*a[R]%P+a[L]*a[R]%P*2%P)%P)%=P;
return;
}
ll mid=(L+R)>>1;
ll mi=a[mid],mx=a[mid];
ll j=mid,k=mid;
ll Mi=a[mid+1],Mx=a[mid+1];
s1[0][mid]=s2[0][mid]=s3[0][mid]=0;
s1[1][mid]=s2[1][mid]=s3[1][mid]=0;
for(ll i=mid+1;i<=R;i++)//预处理出前缀和
{
Mi=min(Mi,a[i]);
Mx=max(Mx,a[i]);
(s1[0][i]=s1[0][i-1]+(i-mid)*Mi%P)%=P;
(s2[0][i]=s2[0][i-1]+(i-mid)*Mx%P)%=P;
(s3[0][i]=s3[0][i-1]+(i-mid)*Mi*Mx%P)%=P;
(s1[1][i]=s1[1][i-1]+Mi)%=P;
(s2[1][i]=s2[1][i-1]+Mx)%=P;
(s3[1][i]=s3[1][i-1]+Mi*Mx%P)%=P;
}
ll i=mid;
while(i>=L)
{
mi=min(mi,a[i]);
mx=max(mx,a[i]);
while(a[j+1]>mi&&j<R)j++;//注意判断是否越界,或者边界设为INf
while(a[k+1]<mx&&k<R)k++;
ll w1=min(j,k);
ll w2=max(j,k);
if(w1>mid)(ans+=mi*mx%P*((mid+1-i+1+w1-i+1)*(w1-(mid+1)+1)/2%P)%P)%=P;
if(k>j)
{
(ans+= mx*( (s1[0][k]-s1[0][j]+P)%P + (mid-i+1)*(s1[1][k]-s1[1][j]+P)%P)%P)%=P;
}
if(j>k)
(ans+=mi*((s2[0][j]-s2[0][k]+P)%P+(mid-i+1)*(s2[1][j]-s2[1][k]+P)%P)%P)%=P;
(ans+= ((s3[0][R]-s3[0][w2]+P)%P + (mid-i+1)*(s3[1][R]-s3[1][w2]+P)%P)%P)%=P;
i--;
}
Estar(L,mid);
Estar(mid+1,R);
}
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%lld",&a[i]);
}
Estar(1,n);
printf("%lld",ans%P);
return 0;
}
后面都是是一些简单的水题。
前缀和&差分
参考资料:oiwiki
前缀和
前缀和可以简单理解为「数列的前\(n\)项的和」,是一种重要的预处理方式,能大大降低查询的时间复杂度。
二维/多维前缀和
一般来讲是运用容斥原理来解决。不一般的比如说基于DP的高位前缀和,有兴趣自己bdfs一下,这里就不讲了 ╮(・o・)╭
放个小题:P1387 最大正方形
因为是01矩阵,所以可以想二维前缀和表示该区域内1的个数。
题目要求的是最大的全部为1的正方形,那就可以枚举边长l,
判断一个是否有边长为l的正方形满足。
附上代码:
#include<bits/stdc++.h>
using namespace std;
int a[103][103];
int b[103][103];
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
b[i][j]=b[i][j-1]+b[i-1][j]-b[i-1][j-1]+a[i][j]; // 求前缀和
}
}
int ans=1;
int l=2;
while(l<=min(n, m))
{
for(int i=l;i<=n;i++)
{
for(int j=l;j<=m;j++)
{
if(b[i][j]-b[i-l][j]-b[i][j-l]+b[i-l][j-l]==l*l)
{
ans=max(ans,l);
}
}
}
l++;
}
printf("%d",ans);
return 0;
}
树上前缀和

边权默认赋给了下方节点。
差分
差分可以看做前缀和的逆运算,也就是说对差分取前缀和就可以得到原序列。
差分性质
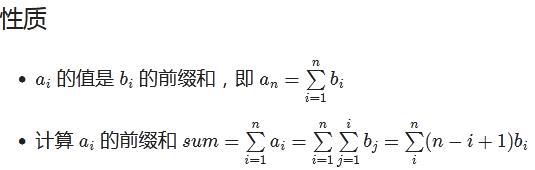
它可以维护多次对序列的一个区间加上一个数,并在最后询问某一位的数或是多次询问某一位的数。注意:修改操作一定要在查询操作之前。
例子:
使序列\([L,R]\)加上val,则\(b[L]+=k,b[R+1]-=k\)
树上差分
树上差分可以理解为对树上的某一段路径进行差分操作,这里的路径可以类比一维数组的区间进行理解。例如在对树上的一些路径进行频繁操作,并且询问某条边或者某个点在经过操作后的值的时候,就可以运用树上差分思想了。
树上差分通常会结合 树基础 和 最近公共祖先 来进行考察。树上差分又分为点差分 与 边差分,在实现上会稍有不同。
点差分
例子:
对树上的一些路径进行访问,问一条路径上的点被访问的次数。
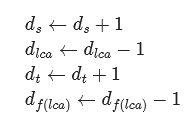
前两个式子是在给下面蓝色框中的式子执行加+1操作;
后两个式子是在给红色框中的式子执行加+1操作。
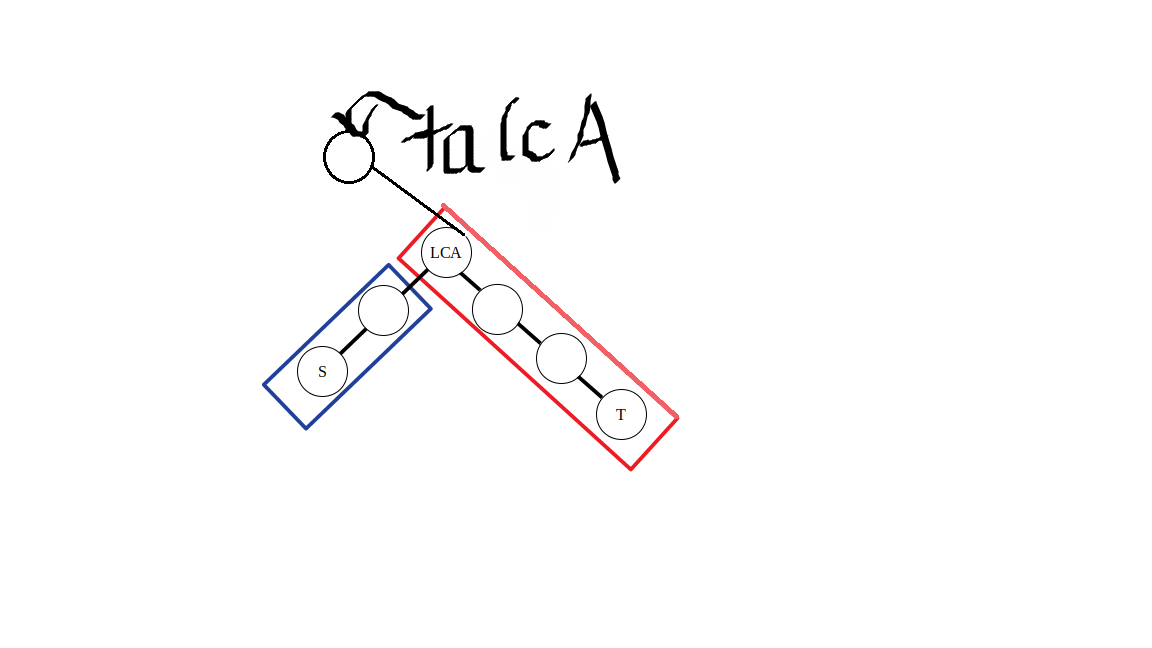
边差分
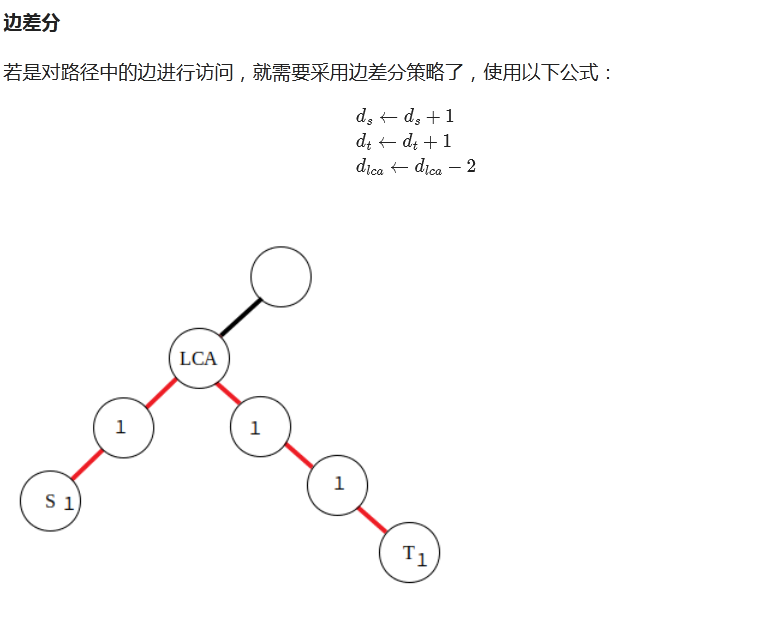
把边抽象称点(并用下面的节点来表示“边”这个“抽象点”的信息),结合上面差分的内容显然能推出上面的式子。
例题:
P3128 Max Flow P
我没做
二分&三分
二分
二分查找:
人生建议:建议不要听取别人的人生建议
一般来讲人们喜欢用STL来进行二分查找,但如果你喜欢手写,那code:
int binary_search(int start, int end, int key)
{
int ret = -1; // 未搜索到数据返回-1下标
int mid;
while (start <= end)
{
mid = start + ((end - start) >> 1); // 直接平均可能会溢出,所以用这个算法
if (arr[mid] < key)start = mid + 1;
else if (arr[mid] > key)end = mid - 1;
else // 最后检测相等是因为多数搜索情况不是大于就是小于
{
ret = mid;
break;
}
}
return ret; // 单一出口
}
如果你喜欢STL,那:
1.binary_search:查找某个元素是否出现。
2.lower_bound:查找第一个大于或等于某个元素的位置。
3.upper_bound:查找第一个大于某个元素的位置.
温馨提示:请保证使用STL时,序列单调。
详解:
1.binary_search:查找某个元素是否出现。
a.函数模板:binary_search(arr[],arr[]+size , indx)
b.参数说明:
arr[]: 数组首地址
size:数组元素个数
indx:需要查找的值
c.函数功能: 在数组中以二分法检索的方式查找,若在数组(要求数组元素非递减)中查找到indx元素则真,若查找不到则返回值为假。
2.lower_bound:查找第一个大于或等于某个元素的位置。
a.函数模板:lower_bound(arr[],arr[]+size , indx):
b.参数说明:
arr[]: 数组首地址
size:数组元素个数
indx:需要查找的值
c.函数功能: 函数lower_bound()在first和last中的前闭后开区间进行二分查找,返回大于或等于val的第一个元素位置(注意是地址)。如果所有元素都小于val,则返回last的位置
d.举例如下:
一个数组number序列为:4,10,11,30,69,70,96,100.设要插入数字3,9,111.pos为要插入的位置的下标,则
/注意因为返回值是一个指针,所以减去数组的指针就是int变量了/
pos = lower_bound( number, number + 8, 3) - number,pos = 0.即number数组的下标为0的位置。
pos = lower_bound( number, number + 8, 9) - number, pos = 1,即number数组的下标为1的位置(即10所在的位置)。
pos = lower_bound( number, number + 8, 111) - number, pos = 8,即number数组的下标为8的位置(但下标上限为7,所以返回最后一个元素的下一个元素)。
e.注意:函数lower_bound()在first和last中的前闭后开区间进行二分查找,返回大于或等于val的第一个元素位置。如果所有元素都小于val,则返回last的位置,且last的位置是越界的!
返回查找元素的第一个可安插位置,也就是“元素值>=查找值”的第一个元素的位置
3.upper_bound:查找第一个大于某个元素的位置。
a.函数模板:upper_bound(arr[],arr[]+size , indx):
b.参数说明:
arr[]: 数组首地址
size:数组元素个数
indx:需要查找的值
c.函数功能:函数upper_bound()返回的在前闭后开区间查找的关键字的上界,返回大于val的第一个元素位置
例如:一个数组number序列1,2,2,4.upper_bound(2)后,返回的位置是3(下标)也就是4所在的位置,同样,如果插入元素大于数组中全部元素,返回的是last。(注意:数组下标越界)
返回查找元素的最后一个可安插位置,也就是“元素值>查找值”的第一个元素的位置。
搬过来果然还是太丑了,原文链接click here
二分答案
解题的时候往往会考虑枚举答案然后检验枚举的值是否正确。若满足单调性,则满足使用二分法的条件。把这里的枚举换成二分,就变成了「二分答案」。
一般来讲,题目中出现“最小值最大,最大值最小”等需要用到二分答案。
每个人有每个人的二分模板啦,这里就不贴我的了。
三分法
如果需要求出单峰函数的极值点,通常使用二分法衍生出的三分法求单峰函数的极值点。
大体思想:左右各取一个点(取\(mid-eps\)和\(mid+eps\)是不错的选择),再删去左侧或右侧不符合的区间。
P3382 【模板】三分法
这个题的题解区很乱搞,模拟退火都上场了……
还是,附上代码:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll N=20;
const double eps=1e-6;
ll n;
double l,r,a[N];
double F(double x)
{
double ans=0;
for(ll i=n;i>=0;i--) ans=ans*x+a[i];
return ans;
}
int main()
{
scanf("%lld%lf%lf",&n,&l,&r);
for(ll i=n;i>=0;i--)
scanf("%lf",&a[i]);
while(r-l>eps)
{
double mid=(l+r)/2;
if(F(mid+eps)>F(mid-eps)) l=mid;
else r=mid;
}
printf("%.5lf",l);
return 0;
}
倍增
简介:可以优化时间复杂度,常见问题: RMQ 问题和求 LCA(最近公共祖先)。
ST表
ST 表是用于解决 可重复贡献问题的数据结构(数据结构?那貌似我可以不讲?)。
突然发现这和某位要讲的重复了,那就不讲了。
对于RMQ问题的求解
预处理部分:

查询部分:

LCA
LCA也是倍增的,也重复了,噢耶。

构造
嗯?高自由度?


简介:
构造题是比赛中常见的一类题型。
从形式上来看,问题的答案往往具有某种规律性,使得在问题规模迅速增大的时候,仍然有机会比较容易地得到答案。
这要求解题时要思考问题规模增长对答案的影响,这种影响是否可以推广。例如,在设计动态规划方法的时候,要考虑从一个状态到后继状态的转移会造成什么影响。
特点:
简而言之:看智商看人品
构造题一个很显著的特点就是高自由度,也就是说一道题的构造方式可能有很多种,但是会有一种较为简单的构造方式满足题意。看起来是放宽了要求,让题目变的简单了,但很多时候,正是这种高自由度导致题目没有明确思路而无从下手。
构造题另一个特点就是形式灵活,变化多样。并不存在一个通用解法或套路可以解决所有构造题,甚至很难找出解题思路的共性。
来几道好玩的题:
P3599 Koishi Loves Construction
官方的回答了他的废话

这启示我们什么?
大胆想象,大胆猜测,勇夺第一,实创辉煌。
完结,撒花啦✿✿ヽ(°▽°)ノ✿
等等,你以为完了吗?实际上还有一篇

 学案1
学案1
