复分析 个人笔记(期末复习向)
课程教材:《Stein 复分析》,章节、题号均指该教材。
所有定理全文默写且会用!!!
第一章 复分析基本概念
定义
- \(z=x+iy=re^{i\theta}\)
- \(\mathrm{Re}z=x\):\(z\) 的实部
- \(\mathrm{Im}z=y\):\(z\) 的虚部
- \(\overline{z}=x-iy\):\(z\) 的共轭
- \(|z|=\sqrt{x^2+y^2}\):\(z\) 的模长
- \(\arg z = \theta\in [0,2\pi)\):\(z\) 的辐角
- 欧拉公式 \(e^{i\theta} = \cos\theta+i\sin \theta\)
- 复指数函数 \(e^z = e^{x+iy} = e^x\cos y + ie^x\sin y\)
- 复三角函数 \(\cos z = \dfrac {e^{iz}+e^{-iz}}2, \sin z = \dfrac{e^{iz}-e^{-iz}}{2i}\)
- \(D(z_0,r)\):以 \(z\) 为圆心,\(r\) 为半径的开圆盘,即 \(D(z_0,r) = \{z:|z-z_0|<r\}\)
- \(D_r = D(r) = D(0,r), C_r = \partial D_r\)
- \(\mathbb{D}=D(0,1)\):单位圆盘
- \(\overline{D}\):区域 \(D\) 的闭包
- \(\partial D\):区域 \(D\) 的边界,逆时针方向
- \([z,w]\):以 \(z,w\) 为端点的线段(起点是 \(z\))
- \(\gamma: z=z(t),t\in [a,b]\):复平面上的一条曲线,\(z(a)=z(b)\) 就是闭曲线
- \(\int_\gamma f(z)dz\):曲线积分,\(\int_\gamma f(z)dz = \int_a^bf(z(t))z'(t)dt = F(z(b))-F(z(a))\)(\(F\) 为 \(f\) 的原函数,即 \(F'(z)=f(z)\)。但是 \(F\) 不一定存在)
- 常函数:\(f(z)=C\)
- 全纯函数(holomorphic function):\(f'(z)=\lim_{h\rightarrow 0}\frac {f(z+h)-f(z)}h\) 处处存在。注意只能称一个函数在一个开集上全纯,有边界点的是不可以的。
- 整函数:在复平面 \(\mathbb{C}\) 上全纯的函数
- 单连通区域:
任意两条曲线同伦可以简单理解为没有洞的区域
定理 0. Cauchy-Riemann 方程
设 \(f\) 在 \(z_0\) 全纯,则
题
-
\(\star\) 给定 \(w\in \mathbb{D}\),证明函数 \(F(z) = \dfrac {w-z}{1-\overline{w}z}\) 满足下列性质:
- \(F: \mathbb{D}\rightarrow \mathbb{D}\) 且全纯
- \(F(0)=w,F(w)=0\)
- 若 \(|z|=1\),则 \(|F(z)|=1\)
- \(F\) 是双射
解答:Ex 1.7(b)
-
\(\sharp\) 设 \(f\) 在开集 \(\Omega\) 上全纯,\(|f|\) 为常值,证明 \(f\) 为常函数。
解答:Ex 1.13(b)
第二章 Cauchy 定理及其应用
定理 1. Cauchy 定理(Cauchy's theorem)
设 \(f\) 在圆盘 \(D\) 上全纯,闭曲线 \(\gamma\subset D\),则
推论 1.
设 \(f\) 在包含圆周 \(C\) 及其内部的区域上全纯,则
应用
在求积分的时候可以把积分区域补成闭曲线,且满足被积函数在闭曲线里围成的区域中全纯。答案就是另几条边的积分的相反数。
一般积分区域是 \(\mathbb{R}\) 都会转成极限然后补成半圆或者矩形,\(\mathbb{R}^+\) 补成扇形或者矩形。
选取闭曲线时,另外几条边的积分一般是 \(0\) 或很容易计算的实积分。
定理 2. Cauchy 积分公式(Cauchy integral formula)
设 \(f\) 在包含圆盘 \(D\) 的闭包的一个开集中全纯,\(\partial D\) 为 \(D\) 的正向边界曲线,则
推论.
定理 3. Cauchy 不等式(Cauchy inequalities)
设 \(f\) 在包含圆盘 \(D(z_0,R)\) 的一个开集中全纯,则
其中 \(\Vert f\Vert_{\partial D} = \sup_{z\in \partial D}|f(z)|\)。
定理 4. Liouville 定理(Liouville's theorem)
设 \(f\) 是有界整函数,则 \(f\) 是常函数。
定理 5. 解析延拓原则(analytic continuation)
设 \(f\) 在区域 \(\Omega\) 上全纯,存在 \(z_0\in \overline\Omega\) 和 \(\{z_n\}\subset \Omega\) 满足 \(\{z_n\}\) 两两不同且 \(\lim_{n\rightarrow \infty}z_n=z_0\),则 \(f=0\)。
推论.
设 \(f\) 和 \(g\) 都在 \(\Omega\) 上全纯且在 \(\Omega\) 的非空开子集 \(\Omega'\) 上相等(或者在一个收敛点列上相等),则 \(f(z)=g(z),\forall z\in \Omega\)。因此如果 \(f\) 本身定义在 \(\Omega'\) 上而 \(g\) 定义在 \(\Omega\) 上,就可以将 \(f\) 的定义拓展到 \(\Omega\)。即称 \(g\) 为 \(f\) 的解析延拓。
复积分的二级结论
-
\(\int_{\partial\mathbb{D}}z^ndz=0, n\in \mathbb{Z},n\neq -1\)
-
\(\int_{\partial\mathbb{D}}z^{-1}dz = 2\pi i\)
-
\(\int_0^{\infty}e^{-x^2}dx = \sqrt \pi\)
-
\(\int_0^{\infty} \frac{\sin x}x = \frac {\pi}2\)
题
-
\(\star\) 证明
\[\int_0^\infty \sin(x^2)dx = \int_0^\infty \cos(x^2)dx = \frac {\sqrt{2\pi}}4 \]解答:Ex 2.1
-
\(\star\) 证明
\[\int_0^{\infty} \frac{\sin x}xdx = \frac{\pi}2. \]解答:Ex 2.2
-
\(\star\) 设 \(f\) 在带状区域 \(\Omega=\{-1<y<1,x\in \mathbb{R}\}\) 上全纯,且
\[|f(z)|\leq A(1+|z|)^{\eta}, \eta\in \mathbb{R},\forall z \]证明对任意整数 \(n\geq 0\),存在 \(A_n\geq 0\) 使得
\[|f^{(n)}(x)|\leq A_n(1+|x|)^\eta, \forall x\in \mathbb{R} \]解答:Ex 2.8
-
\(\sharp\) 计算
解答:Ex 2.3
第三章 半纯函数和对数函数
定义
-
半纯函数(meromorphic function):除可数个极点外全纯
-
奇点(singular):\(f\) 不全纯的点
- 可去奇点(removable singularities):\(|f(z)|\rightarrow A(z\rightarrow z_0)\),可补充定义 \(f(z_0)=A\) 使 \(f\) 在 \(z_0\) 处全纯(因此不妨假定 \(f\) 没有可去奇点)。
- 极点(poles):\(|f(z)|\rightarrow \infty(z\rightarrow z_0)\)
- 单极点(simple pole):\(|f(z)|\rightarrow \infty(z\rightarrow z_0),(z-z_0)f(z_0)=A\)
- \(m\) 阶极点:\((z-z_0)^{m-1}f(z_0)\rightarrow \infty(z\rightarrow z_0)\),但 \((z-z_0)^m f(z_0) = A\)
- \(f\) 的 \(m\) 阶极点等价于 \(\frac 1f\) 的 \(m\) 阶零点
-
本性奇点(essential singularities):对任意 \(n\),\((z-z_0)^nf(z_0)\rightarrow \infty(z\rightarrow z_0)\)(本章不讨论)
-
(\(f\) 在奇点 \(z_0\) 处的)留数(residue):将 \(f(z)\) 在 \(z_0\) 处展开成有理级数(本性奇点 \(m=\infty\))
\[f(z) = \sum_{n=-m}^{\infty}a_n(z-z_0)^n \]记 \(\mathrm{res}_{z_0}f = a_{-1}\)。
-
极点处留数的计算公式:设 \(z_0\) 为 \(f\) 的 \(m\) 阶极点,则
\[\mathrm{res}_{z_0}f = \lim_{z\rightarrow z_0}\frac 1{(m-1)!}\frac{d^{m-1}}{dz^{m-1}}(z-z_0)^mf(z). \]一般只需要用到 \(m=1,2\) 的情况:
\[\begin{aligned} m=1, & \mathrm{res}_{z_0}f = (z-z_0)f(z)|_{z=z_0} \\ m=2, & \mathrm{res}_{z_0}f = ((z-z_0)^2f(z))'|_{z=z_0} \end{aligned} \] -
复对数:多值函数,因为 \(\log z = \log(re^{i\theta})=\log r+i\theta\),而 \(\theta\) 是多值的。
- 在不含原点的单连通区域(例如半平面、半圆盘、 \(\mathbb{C}\backslash(-\infty,0]\) 等)上可以全纯定义。
定理 6. 留数定理(Residue Theorem)
设 \(f\) 在包含闭曲线 \(\gamma\) 及其内部区域的开集 \(\Omega\) 上半纯,极点为 \(z_1,\dots,z_N\),则
应用
比 Cauchy 定理更强的公式,不需要区域内全纯,只需要区域内半纯即可。
但是注意用留数时极点只能落在区域内或者区域外。如果极点在边界上就用不了了。
对区域的选取:
- 同 Cauchy 定理,一般考虑补成半圆计算 \(\mathbb{R}\) 上积分或者补成 1/4 扇形计算 \(\mathbb{R}^+\) 上积分。
- 如果积分曲线上存在极点,用一个小圆弧“绕开”它。
对圆弧积分的计算,可以用下面两个引理(可直接使用):
- 大圆弧引理:设 \(f(z)\) 在 \(L: z=z_0+\rho e^{i\theta}, \theta\in [\alpha,\beta]\) 上连续,且 \(\lim_{z\rightarrow \infty} (z-z_0)f(z) = A\),则 \(\lim_{\rho\rightarrow \infty} \int_L f(z)dz = i(\beta-\alpha)A\)
- 小圆弧引理:设 \(f(z)\) 在 \(L: z=z_0+\rho e^{i\theta}, \theta\in [\alpha,\beta]\) 上连续,且 \(\lim_{z\rightarrow z_0} (z-z_0)f(z) = A\),则 \(\lim_{\rho\rightarrow 0} \int_L f(z)dz = i(\beta-\alpha)A\)
- Jordan 引理:设 \(f(z)\) 在 \(L: z=\rho e^{i\theta}, \mathrm{Im}z\geq 0\) 上连续,且 \(\lim_{z\rightarrow \infty, \mathrm{Im}z\geq 0}f(z) = 0\),则 \(\forall \lambda > 0, \lim_{\rho\rightarrow \infty}\int_L f(z)e^{\lambda iz}dz = 0\)。
留数的题
-
\(\star\) 证明
\[\int_{-\infty}^{\infty} \frac{\cos x}{x^2+a^2}dx = \pi\frac{e^{-a}}a,a>0. \]解答:Ex 3.3
-
\(\star\) 证明
\[\int_0^{2\pi} \frac{d\theta}{a+b\cos\theta}=\frac{2\pi}{\sqrt{a^2-b^2}}. \]解答:Ex 3.8
-
\(\sharp\) 证明
\[\int_{-\infty}^\infty \frac{dx}{(1+x^2)^{n+1}}=\frac{(2n-1)!!}{(2n)!!}\pi. \]解答:Ex 3.6
-
计算
\[\int_{-\infty}^{\infty}\frac{x\sin x}{x^2+a^2}dx. \]![]()
-
证明对任意 \(c>0\),
\[\frac 1{2\pi i}\int_{c-i\infty}^{c+i\infty}\frac{y^s}{s^2}ds = \begin{aligned}&\log y, & y\geq 1, \\ &0, & 0<y<1.\end{aligned} \]![]()
-
\(a>0,\mathrm{Re}(s)>0\),计算
\[\int_0^{+\infty}\frac{x^s}{x^2+a^2}dx \]![]()
(实部等于 1 发散我不确定,可能虚部要满足一些条件才发散。不会证)
定理 7. 辐角原理(Argument Principle)
设 \(f\) 在包含闭曲线 \(C\) 及其内部区域的开集上半纯,且 \(f\) 在 \(C\) 上没有零点和极点,则
推论(广义辐角原理)
定理 8. Rouche 原理(Rouche's throrem)
设 \(f\) 和 \(g\) 在包含闭曲线 \(C\) 及其内部区域的开集上半纯,且
则 \(f\) 和 \(f+g\) 在 \(C\) 中的零点数相等。
定理 9. 极大模原理(Maximum modulus principle)
设 \(f\) 在区域 \(\Omega\) 中全纯且非常值,则 \(|f|\) 在 \(\Omega\) 内部取不到最大值。即
题
-
\(\star\) 利用 Cauchy 不等式或极大值原理证明:
- 若 \(f\) 在 \(\mathbb{D}\) 内部全纯有界,且在扇形区域 \(\theta<\arg z<\varphi\) 上当 \(|z|\rightarrow 1\) 时一致收敛于零,则 \(f=0\)。
- 设 \(w_1,\dots,w_n\in \mathbb{D}\), 证明 \(\exists z\in \mathbb{D}, \prod_{j=1}^n |z-w_j|\geq 1\)。
解答:Ex 3.15 (b)(c)
-
\(\star\) 设 \(f,g\) 在包含 \(\overline{\mathbb{D}}\) 的区域上全纯且在 \(\overline{\mathbb{D}}\) 上只有一个一阶零点 \(z=0\)。记 \(f_\epsilon(z) = f(z) + \epsilon g(z)\)。证明:当 \(\epsilon\) 充分小时,有
- \(f_{\epsilon}(z)\) 在 \(\overline{\mathbb{D}}\) 上只有一个一阶零点
- 若 \(z_{\epsilon}\) 是上一问中的零点,则映射 \(\epsilon\rightarrow z_\epsilon\) 连续。
解答:Ex 3.16
-
设 \(a>1\),证明 \(ze^{a-z}=1\) 在 \(\mathbb{D}\) 上有且仅有一个根,且为正实数。
解答:令 \(f(z) = ze^{a-z}, g(z) = -1\),则
\[|f(z)|=|ze^{a-z}|=|z||e^{a-z}|=e^{a-\mathrm{Re}(z)}> e^{a-1}=1, \forall z\in \partial \mathbb{D}. \]因此 \(|f|>|g|, \forall z\in \partial\mathbb{D}\)。
由 Rouche 定理,\(ze^{a-z}-1=0\) 和 \(ze^{a-z}=0\) 在 \(\mathbb{D}\) 上有相同数量的根。
显然 \(ze^{a-z}=0\) 有唯一根 \(z=0\),因此 \(ze^{a-z}-1=0\) 在 \(\mathbb{D}\) 上也只有一个根。
考虑 \(\mathbb{R}\) 上的函数 \(f(x) = xe^{a-x}\)。因为 \(f(0)=0<1, f(1)=e^{a-1}>1\),由连续函数的介值定理知 \(f(x)=1\) 在 \((0,1)\) 上存在至少一个根。结合前面结论得 \(f\) 在 \(\mathbb{D}\) 上的唯一根为正实根。证毕。
第五章 整函数的零点和阶数
定义
-
整函数的增长阶(order of growth):设 \(f\) 为整函数,若存在 \(\rho>0\) 和 \(A,B>0\) 使得 \(|f(z)|\leq Ae^{B|z|^\rho},\forall z\in \mathbb{C}\),则称 \(f\) 的增长阶 \(\leq \rho\)。即记
\[\rho_f = \inf\{\rho:\exists A,B>0,\text{s.t.}|f(z)|\leq Ae^{B|z|^\rho},\forall z\in\mathbb{C}\} \]例如多项式函数的增长阶为 \(0\),\(e^{z^2}\) 的增长阶为 \(2\),\(e^{e^z}\) 的增长阶为 \(\infty\)。
-
典范因子(canonical factor):\(E_0(z) = 1-z, E_k(z) = (1-z)e^{z+z^2/2+\dots+z^k/k}, k\geq 1.\)
定理 10. Jensen 公式(Jensen's formula)
设 \(\Omega\) 为包含圆盘 \(D_R\) 及其边界的开集,\(f\) 在 \(\Omega\) 上全纯,\(f(0)\neq 0\),\(f\) 在 \(C_R\) 上非零。
若 \(z_1,\dots,z_N\) 是 \(f\) 在 \(D\) 中的零点(计重数,即 \(m\) 重零点会加 \(m\) 次),则
定理 11. Hardmard 因子分解定理(Hardmard's factorization theorem)
设 \(f\) 是增长阶为 \(\rho_0\) 的整函数,\(k = \lfloor \rho_0\rfloor\),\(\{a_n\}\) 为 \(f\) 的全体零点,则
其中 \(P\) 为次数不超过 \(k\) 的多项式,\(m\) 为 \(0\) 的重数。
常用二级结论
题
-
\(\star\) 证明当 \(\alpha > 1\) 时,\(F_\alpha(z) = \int_{-\infty}^\infty e^{-|t|^\alpha}e^{2\pi izt}dt\) 是增长阶为 \(\frac \alpha{\alpha-1}\) 的整函数。
解答:Ex 5.5
-
\(\star\) 求下列函数的 Hardmard 因子分解:
- \(e^z-1\)
- \(\cos \pi z\)
解答:Ex 5.10
-
\(\star\) 利用 Hardmard 因子分解定理证明:若 \(F\) 是整函数且增长阶不是整数,则 \(F\) 有无穷多个零点。
解答:Ex 5.14
-
\(\sharp\) 证明方程 \(e^z-z=0\) 有无穷多复数根。
解答:Ex 5.13
-
证明若 \(f\) 在 \(\mathbb{D}\) 中有界全纯且不恒等于 \(0\),\(\{z_n\}\) 为 \(f\) 的零点,则
\[\sum_n(1-|z_n|)<\infty. \]![]()
-
证明对任意 \(|x|<1\) 有
\[\prod_{n=0}^{\infty}(1-x^{5n+1})(1-x^{5n+4})(1-x^{5n+5})=\sum_{n=-\infty}^\infty (-1)^nx^{\frac{n(5n+3)}2} \]这题不会((
第六章 \(\Gamma\) 函数和 \(\zeta\) 函数
定义
-
\(\Gamma\) 函数(Gamma function):对任意右半平面 \(\{\mathrm{Re}(s)>0\}\) 的复数 \(s\),定义
\[\Gamma(s) = \int_0^\infty e^{-t}t^{s-1}dt. \]简单性质:
-
\(\Gamma(1) = 1, \Gamma(\frac 12) = \sqrt\pi\)
-
\(\Gamma(s+1) = s\Gamma(s), \forall \mathrm{Re}(s)>0\)
-
-
欧拉常数(Euler's constant):\(\gamma = \lim_{N\rightarrow \infty}\sum_{n=1}^N\frac 1n - \log N\)
-
\(\zeta\) 函数(zeta function):对任意半平面 \(\{\mathrm{Re}(s)>1\}\) 的复数 \(s\),定义
\[\zeta(s) = \sum_{n=1}^\infty \frac 1{n^s}. \] -
\(\xi\) 函数(xi function):对任意半平面 \(\{\mathrm{Re}(s)>1\}\) 的复数 \(s\),定义
\[\xi(s) = \pi^{-s/2}\Gamma(s/2)\zeta(s). \]
定理 12. \(\Gamma\) 函数的乘积公式
对任意 \(s\in \mathbb{C},\mathrm{Re}(s)>0\),有
这个乘积公式表明,\(\Gamma\) 函数可以延拓为 \(\mathbb{C}\) 上的半纯函数,且仅在 \(0,-1,-2,\dots\) 上有单极点。
定理 13. \(\zeta\) 函数的函数方程
\(\xi\) 函数在半平面 \(\mathrm{Re}(s)>1\) 上全纯,且可解析延拓到复平面 \(\mathbb{C}\) 上的极点为 \(s=0\) 和 \(s=1\) 的半纯函数。进一步有
进一步地,\(\zeta\) 函数也可以延拓为 \(\mathbb{C}\) 上的半纯函数。
题
-
\(\star\) 对任意 \(\mathrm{Re}(\alpha)>0,\mathrm{Re}(\beta)>0\),定义 Beta 函数:
\[B(\alpha,\beta) = \int_0^1(1-t)^{\alpha-1}t^{\beta-1}dt \]- 证明 \(B(\alpha,\beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}.\)
- 证明 \(B(\alpha,\beta) = \int_0^{\infty} \frac{u^{\alpha-1}}{(1+u)^{\alpha+\beta}}du.\)
解答:Ex 6.7
-
\(\star\) 证明对任意 \(\mathrm{Re}(s)>1\),有
\[\zeta(s) = \frac 1{\Gamma(s)}\int_0^\infty\frac{x^{s-1}}{e^x-1}dx. \]解答:Ex 6.13
-
定义 Bernoulli 数:
\[\sum_{m=0}^\infty \frac{B_m}{m!}x^m = \frac x{e^x-1} \]证明:
\[\zeta(2k)= \frac{(-1)^{k-1}2^{2k-1}}{(2k)!}x^{2k}B_{2k}. \]解答:
![]()
-
证明
\[\begin{aligned} \zeta(s) =& \frac 1{\Gamma(s)}\int_0^{\infty}\left(\frac 1{e^x-1}-\frac 1x\right)x^{s-1}dx, 0<\mathrm{Re}(s)<1, \\ \zeta(s) =& \frac 1{\Gamma(s)}\int_0^{\infty}\left(\frac 1{e^x-1}-\frac 1x+\frac 12\right)x^{s-1}dx, -1<\mathrm{Re}(s)<0. \end{aligned} \]不会做(
-
证明:
\[\begin{aligned} \frac 1{e^x-1} =& \frac 1x - \frac 12 + \sum_{n=0}^\infty \frac{2x}{x^2+4n^2\pi^2},\\ \Gamma(s)\zeta(s) =& \frac{\pi^s2^{1-s}}{\cos(\pi s/2)}\zeta(1-s). \end{aligned} \]第一问解答:
![]()
第二问不会做(
-
证明:
\[\psi(s) = \frac{\Gamma'(s)}{\Gamma(s)} = -\gamma - \frac 1s - \sum_{n=1}^{\infty}(\frac 1{n+s} - \frac 1n) \]并验证 \(\psi(1-s)-\psi(s)=\pi\cot(\pi s)\)。
证明:根据 \(\Gamma\) 函数的乘积公式得
\[\frac 1{\Gamma(s)} = e^{\gamma s}s\prod_{n=1}^\infty (1+\frac sn)e^{-\frac sn} \]取对数有
\[\log\Gamma(s) = -\gamma s-\log s+\sum_{n=1}^\infty \frac sn-\log(1+\frac sn). \]求导得
\[\psi(s) = \frac d{ds}\log\Gamma(s) = -\gamma-\frac 1s + \sum_{n=1}^\infty \frac 1n -\frac{\frac 1n}{1+\frac sn}= -\gamma-\frac 1s - \sum_{n=1}^\infty (\frac 1{n+s} - \frac 1n). \]进而有
\[\psi(1-s)-\psi(s) = -\frac 1{1-s} +\frac 1s - \sum_{n=1}^\infty (\frac 1{n+1-s}-\frac 1n-\frac 1{n+s} + \frac 1n) = \sum_{n=-\infty}^\infty \frac 1{n+s} = \pi\cot(\pi s). \]证毕。
-
证明:
\[\frac 4{\sqrt\pi}\int_0^\infty e^{-x^2}\log xdx = -\gamma-2\log 2. \]证明:注意到
\[\begin{aligned} \Gamma(s) = & \int_0^{\infty} t^{s-1}e^{-t} dt, \\ \Gamma'(s) = & \int_0^{\infty}\frac d{ds}t^{s-1}e^{-t} dt = \int_0^{\infty} t^{s-1}e^{-t}\log t dt \\ \end{aligned} \]因此
\[\Gamma'(\frac 12) = \int_0^{\infty} t^{-\frac 12}e^{-t}\log t dt = 4\int_0^\infty e^{-x^2}\log xdx = 4I \]因为(上一题结论)
\[\psi(\frac 12) = \frac{\Gamma'(\frac 12)}{\Gamma(\frac 12)} = -\gamma - 2 - \sum_{n=1}^\infty (\frac 1{n+\frac 12}-\frac 1n) \]所以 \(\frac{4}{\sqrt\pi}I = \psi(\frac 12) = -\gamma-2-\sum_{n=1}^\infty(\frac 1{n+\frac 12}-\frac 1n) = -\gamma-2\sum_{n=1}^\infty\frac{(-1)^{n-1}}n=-\gamma-2\log 2\)。
第九章 椭圆函数初步
定义
-
双周期函数(doubly periodic function):设 \(\omega_1,\omega_2\neq 0\) 实线性无关(即 \(\omega_2/\omega_1\notin \mathbb{R}\)),\(\mathbb{C}\) 上的半纯函数 \(f\) 满足
\[f(z+\omega_1) = f(z+\omega_2) = f(z), \forall z\in \mathbb{C} \]则称 \(f\) 为双周期函数。不妨设 \(\omega_1 = 1, \omega_2 = \tau\)。
- 记 \(\Lambda = \{n+m\tau: n,m\in \mathbb{Z}\}\) 为 \(1\) 和 \(\tau\) 生成(generate)的网格(lattice);
- 记 \(P_0 = \{z: z=a+b\tau, 0\leq a<1, 0\leq b<1\}\) 为基本平行四边形(fundamental parallelogram);
- 称 \(z\) 和 \(w\) 等价,如果 \(z=w+n+m\tau, n,m\in \mathbb{Z}\)。记作 \(z\sim w\)。
- 全纯双周期函数必为常值函数。
-
称非常值双周期函数为椭圆函数(elliptic function),其基本多边形中的极点数量为阶数(order)。
定理 14. Werierstrass \(p\) 函数定义和性质(打不出来那个字母)
- \(p\) 是周期为 \(1\) 和 \(\tau\) 的 \(2\) 阶椭圆函数。
- \(p'(1/2)=p'(\tau/2)=p'((1+\tau)/2)=0\)
- \(p(1/2)=e_1,p(\tau/2)=e_2,p((1+\tau)/2)=e_3\),则 \(p'^2=4(p-e_1)(p-e_2)(p-e_3)\)。
定理 15. Eisenstein 级数(Eisenstein series)及其 Fourier 展开
定义 \(k\) 阶 Eisenstein 级数为
若 \(k\geq 4, \mathrm{Im}(\tau)>0\),则
其中除子函数(divisor function) \(\sigma_l(r)\) 定义为
题
-
\(\star\) 设 \(a_1,\dots,a_r\) 和 \(b_1,\dots,b_r\) 分别是椭圆函数 \(f\) 在基本平行四边形内的零点和极点,证明
\[\sum_{j=1}^r a_j - \sum_{j=1}^r b_j = n\omega_1 + m\omega_2. \]解答:Ex 9.2
-
\(\star\) 设 \(E_4(\tau) = \sum_{(n,m)\neq (0,0)} \frac 1{(n+m\tau)^4}\),证明
- \(E_4(\tau)\rightarrow \frac{\pi^4}{45}(\mathrm{Im}(r)\rightarrow \infty)\)
- \(\left|E_4(\tau) - \frac{\pi^4}{45}\right|\leq ce^{2\pi t}, \tau=x+it, t\geq 1\)
- \(|E_4(\tau)-\tau^{-4}\frac{\pi^4}{45}\leq ct^{-4}e^{-2\pi/t}, \tau=it, 0<t\leq 1\)
解答:Ex 9.8
待过题目
期末:第一题默写,第二题重点原题,第三题非重点原题,第四题没留过的题或和作业类似的题(几乎必出第三章内容)。后三题很难,可以按出题人的提示走两步。
积分题
偶函数带 \(\sin f(z)\) 和 \(\cos f(z)\) 在 \(\mathbb{R}\) 上的积分,先转成 \(e^{if(z)}\),取上半平面的半圆弧积分,然后把奇函数的部分利用对称性消掉;在 \(\mathbb{R}^+\) 上的积分直接转成 \(\mathbb{R}\) 上的然后除 2。不是偶函数的可能要在扇形区域上积。
同时带 e 和 log 的积分,可以套 \(\Gamma\) 函数的导数(第六章的 7)。
尽量化简,例如取一个大扇形套小扇形的围道先骗一下(虽然取完就做不了了)
其他
如果证明的式子和 \(\Gamma\) 有关,可以套一下乘积公式(第六章的 6);和 \(\zeta\) 有关可以套一下函数方程。
要求和就找 \(\pi\cot\pi z\) 的展开式(第六章的题 3 和 5),能做出来就赚(这题量也根本就不是让人有空好好做后几题的)。证明题实在下不了笔就算了。
如有多余时间可以过一遍 网传前五章答案
- Ch1
- 7
- 9,10,13,16,25
- Ch2
- 1,2,8
- 3,4,7,11,12,15
- Ch3
- 3,8,15,16
- 1,2,6,8,11,13,14,17,20,21,22
- 4,5,7,9,10,12
- Ch5
- 5,10,14
- 2,3,4,6,11,12,13
- Prob 1
- Ch6
- 7,15
- 1,2,3,8,9,14,16
- Ch9
- 2,8
- 1,3,4,6,7

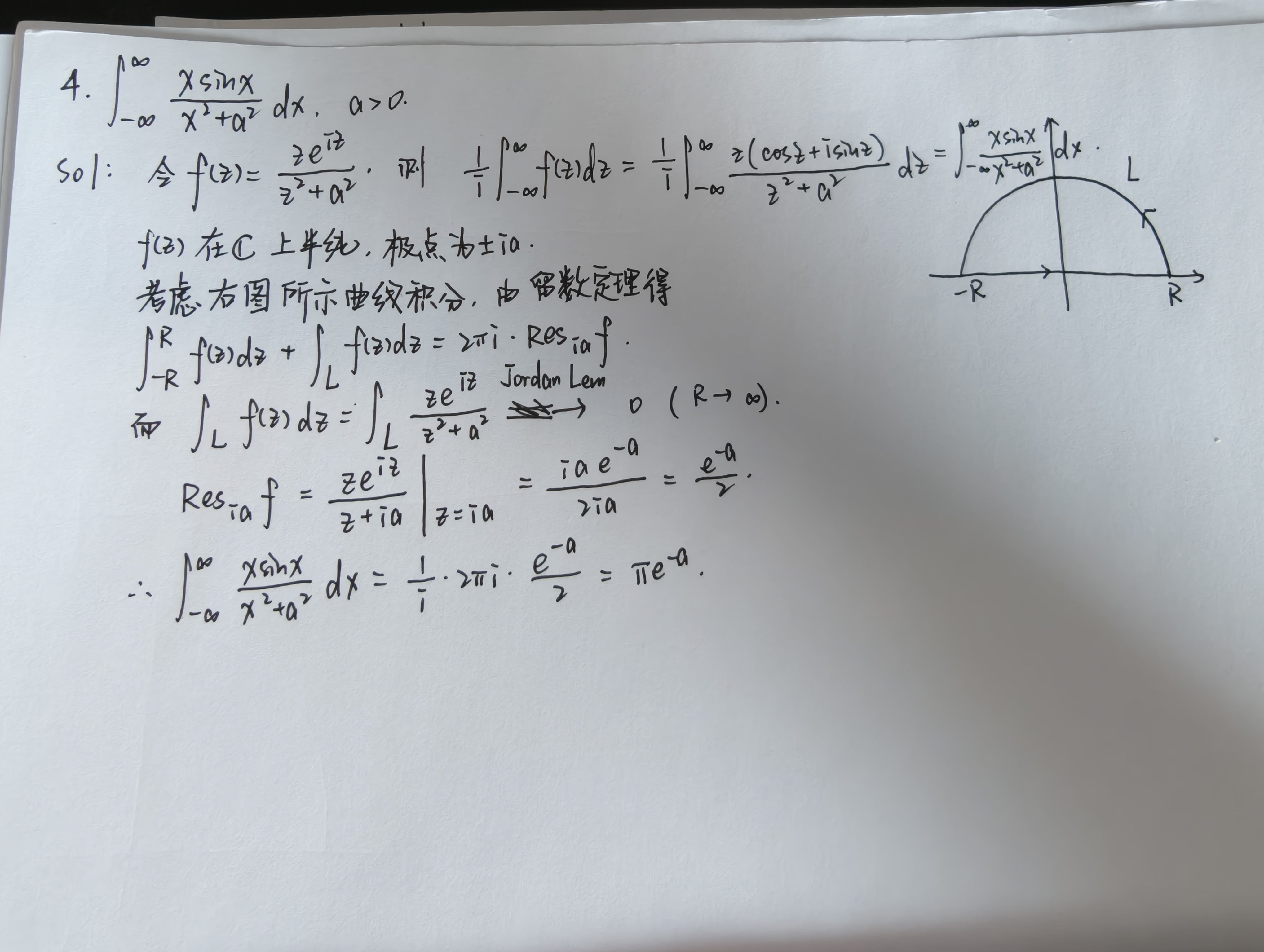






 浙公网安备 33010602011771号
浙公网安备 33010602011771号