[NOI2015]寿司晚宴

目录

• 题面
• 题解
  • 30分做法
  • 60分做法
  • 100分做法
• 总结

---

题面

题意：有两个人要从\([2, n]\)中选数。任意从第一个人选出的数集中挑出一个数，记作a，任意从第二个人选出的数集中挑出一个数，记作b，若对所有的(a, b)，gcd(a, b) =1, 则这种选数方案是合法的。问合法的选数的方案数（答案模\(p\))

---

题解

这道题没什么高深的知识点, 但仍然是一道极好的题.
先从部分分开始分析.

30分做法

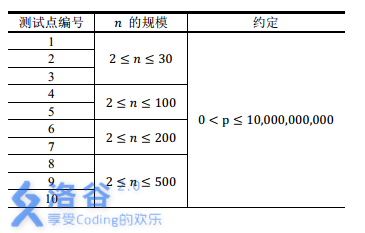
$ n\leq30$
可以想到一个裸的状压DP, 记录

1. Dp至第几位<阶段>
2. 小G选数集合
3. 小W选数集合<对之后状态的影响>
   但是这样会有\(30*2^{60}\)种状态, 太多了
   然而题目只需要关心是否在两人选数集合中有数字不互质
   所以我们在<对之后状态的影响>中只需要记录两人拥有的数的质因子集合就可以了

30以内的质因子有10个， 故复杂度最坏\(O(30*2^{20})\)

\[状态转移方程:\\ f[i][sta_1 | set_i][sta_2] = f[i-1][sta_1 | set_i][sta_2]+f[i-1][sta_1][sta_2]\\ f[i][sta_1][sta_2 | set_i] = f[i-1][sta_1][sta_2 | set_i]+f[i-1][sta_1][sta_2]\\ i表示当前考虑前i个数; sta_1, sta_2表示两人拥有的数的质因子集合;set_i表示整数i的质因子集合 \]

60分做法

不知道有什么做法....应该是100分算法写挂了给的部分分吧....

100分做法

虽然\(n\leq500\) , 但是我们可以发现 \(\sqrt n\lt 23\), 而大于\(\sqrt n\)的素数因子在一个数中只出现一次(或者说可以发现分解每个数并将其化为用二进制表示的集合形式后较高的数位很稀疏)

所以可以把存在大于\(\sqrt n\)素数因子的的数分组, 记作\(S_p\)(\(p\)是那个素因子). \(S_p\)中的每个数去除素因子p之后只剩\(2, 3, 5, 7,11,13,17,19\)这8个素因子。故可以化归为30分做法。

这里放一种错解。(\(\rightarrow\)表示状态的转移, \(S_p.k\)表示\(S_p\)中的第K个元素，\(S1\), \(S2\)为两人取的数所含有的素因子集合的并（当然只考虑小于23的素因子）)

\[f(i-1, s1, s2)\rightarrow f(i, s1|S_p.j,s2), 其中j\le S_p的大小\\ f(i-1, s1, s2)\rightarrow f(i, s1,s2|S_p.j), 其中j\le S_p的大小\\ f(i-1, s1, s2)\rightarrow f(i, s1, s2) \]

这是不对的， 因为这种方法假定\(S_p\)中的元素只能被一个人选取一个。 实际上\(S_p\)中的元素可以被选取多次，但只能被一个人选取。

（所以：这种方法可以通过所有n小于46的情况）

正解如下：

首先，对于存在大于23素因子的数， 我们另外开数组， 用另外一种状态转移的方法。

\[设S_p大小为siz,其他简写沿用上文写法(f_i在此意义是表示第i个阶段,处理一个S_p的过程为一个阶段)\\ 初始化g(0,0,S1, S2)=g(0,1,S1,S2)=f(i-1, S1, S2)\\ g(k-1,0, S1, S2)\rightarrow g(k, 0, S1|S_p.k, S2), 其中k\le siz\\ g(k-1,1, S1, S2)\rightarrow g(k, 1, S1, S2|S_p.k), 其中k\le siz\\ f(i,S1, S2) = g(siz, 0, S1, S2) + g(siz, 1, S1, S2) - f(i-1,S1, S2) \]

最后减掉$ f(i-1,S1, S2)$ 是因为 \(S_p\)中一个数也不取的情况被计算了2次（考虑初始化）

同样G数组也可以滚动掉

对于无大于23素因子的数， 我们只要把其中每个数都看做一个单独的\(S_p\)集合就可以了。

总结

不该犯的错误:
位运算优先级低,必须要加括号!!!这个错误容易避免但是难调

一些常用优化方法：

1. 滚动数组
2. 避免遍历无用状态(如： \(f_{i, s1, s2}\)中\(s1\cup s2 \neq \empty\) 的状态)
3. 根号分治（即：分情况讨论）

#include<bits/stdc++.h>
using namespace std;

#define int long long 
const int primes[] = {2,3,5,7,11,13,17,19};
int n, p;
pair<int,int> num[505];
int f[505][505], g[2][505][505];
int mod(int a){
    return (a + p) % p;
}
signed main(){
    scanf("%lld%lld", &n, &p);
    
    for(int i = 1; i < n; i++){
        int digits = 0, tmp = i+1;
        for(int j = 0; j < 8; j++){
            if(tmp % primes[j] == 0) digits |= 1<<j;
            //printf("%d ",1<<j);
            while(tmp % primes[j] == 0) tmp = tmp/primes[j];
        }
        num[i].first = tmp; num[i].second = digits;
    }

    sort(num+1, num+n);
    f[0][0] = 1;
    for(int i = 1; i < n; i++){
        if(i == 1 || num[i].first==1 || num[i].first != num[i-1].first){
            for(int sta1 = (1 << 8)-1; sta1 >= 0; sta1--){
                for(int sta2 = (1 << 8)-1; sta2 >= 0; sta2--){
                    g[0][sta1][sta2] = g[1][sta1][sta2] = f[sta1][sta2];
                }
            }
        }
        
        for(int sta1 = (1 << 8)-1; sta1 >= 0; sta1--)
            for(int sta2 = (1 << 8)-1; sta2 >= 0; sta2--){
                g[0][sta1 | num[i].second][sta2] = mod(g[0][sta1 | num[i].second][sta2] + 
                    g[0][sta1][sta2]);
                g[1][sta1][sta2 | num[i].second] = mod(g[1][sta1][sta2 | num[i].second] + 
                    g[1][sta1][sta2]);
            }
        if(i == n-1 || num[i].first == 1 || num[i].first != num[i+1].first){
            for(int sta1 = (1 << 8)-1; sta1 >= 0; sta1--)
                for(int sta2 = (1 << 8)-1; sta2 >= 0; sta2--){
                    f[sta1][sta2] = mod(g[0][sta1][sta2] + g[1][sta1][sta2] - f[sta1][sta2]);
                }
        }
    }
    
    int ans = 0;
    for(int sta1 = (1 << 8)-1; sta1 >= 0; sta1--)
        for(int sta2 = (1 << 8)-1; sta2 >= 0; sta2--){
            if((sta1 & sta2) != 0) continue;
            ans = mod(ans + f[sta1][sta2]);
        }
    printf("%lld\n", ans);
    return 0;
}

推荐Sengxian的题解：https://blog.sengxian.com/solutions/bzoj-4197