LeetCode 1137[第N个泰波那契数]

题目

链接

LeetCode 1137[第N个泰波那契数]

详情

实例

实例1

实例2

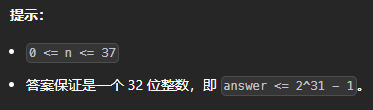
提示

题解

思路一[递归]

当 n 为 0， 1， 2 时，直接返回对应的值

当 n 大于 2 时，开始用 f(n+3) = f(n) + f(n+1) + f(n+2) 来递归求值

代码一[此代码在力扣会超出时间限制]

class Solution {
public:
    int tribonacci(int n) {
        
        if (0 == n)
            return 0;
        
        if ((1 == n) || (2 == n))
            return 1;

        return tribonacci(n - 3) + tribonacci(n - 2) + tribonacci(n - 1);
    }
};

思路二[循环代替递归]

当 n 为 0， 1， 2 时，直接返回对应的值

当 n 大于 2 时，开始用 f(n+3) = f(n) + f(n+1) + f(n+2) 来递归求值

由于递归是不停的复制粘贴，在运行时需要大量的时间，当 n 数值过大时，就会超过力扣官方限制的时间

因此此处采用循环代替递归的方法

此处的循环体为： f(n+3) = f(n) + f(n+1) + f(n+2) 

循环由 3 开始，由 n 结束，依次进入循环体求值，直到求出最后的 f(n) 的值并返回

代码二[此为成功代码]

class Solution {
public:
    int tribonacci(int n) {
        
        if (0 == n)
            return 0;
        
        if ((1 == n) || (2 == n))
            return 1;

        int a0 = 0, a1 = 1, a2 = 1;

        int iRet = 0;

        for (int i = 3; i < n + 1; i++)
        {
            iRet = a0 + a1 + a2;

            a0 = a1;
            a1 = a2;
            a2 = iRet;
        }

        return iRet;
    }
};