圆方树
1 圆方树的定义与性质
圆方树最初是在仙人掌中使用的,后来逐渐被应用到一般图中,用来处理点双联通分量等问题。
一个点双连通图满足的性质有:
- 图中任意两个点都存在至少两条不重复的路径(处理起点和终点),或者说任意去掉其中一个点不能时整张图变成两个不连通的子图,即不存在割点。
- 在一个点双联通图中,对于任意点双中的不同的点 \(s,t\),一定存在一条路径 \(s\rightarrow x\rightarrow t\) 只经过路径上的点一次。
而点双联通分量是极大的点双联通子图。注意,一个孤点是一个点双联通分量,只有两个点的边也是一个点双,每个点至少属于一个点双联通分量,可能属于多个点双联通分量。
在圆方树中,我们对于每个点双连通分量建立一个虚点与所有点连边,代替原本他们之间原有的边,称原图中点的点为“圆点”,新建的虚点为“方点”,那么新建立出的那棵树就被叫做“圆方树”。
\(\bigstar\texttt{Important-1}\):两个割点之间也会形成一个点双,所以在圆方树上方点与圆点交错出现,只存在“方圆边”,不存在“圆圆边”或者“方方边”。
\(\bigstar\texttt{Important-2}\):圆方树会建立很多新的点,所以不要忘记给数组开两倍!
下面这张 WC 讲课的图就非常形象地描述了圆方树构建的过程:
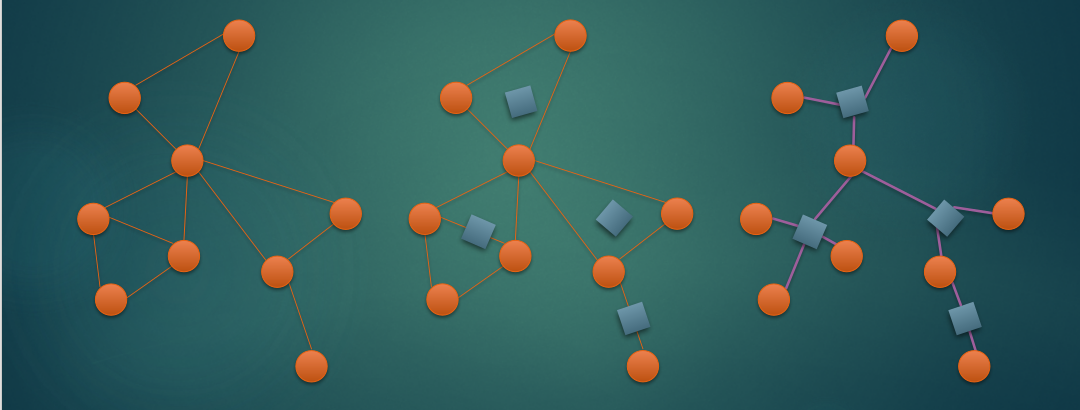
2 圆方树的构建
要建立圆方树,就必须求出点双。啊!那就请来 Tarjan 老爷吧!(不会 tarjan 请左转强联通分量)
求点双联通分量借助 tarjan 的 dfn 和 low,他们的定义如下:
- dfn:在 dfs 过程中第一次遍历到 \(x\) 节点的时间戳;
- low:在 dfs 树中,以 \(x\) 为根的子树中的点的 dfn 和子树内的点可以通过最多一条边到达的最小的 dfn 的较小值。
可以发现,如果以 \(x\) 为根的子树中,通过最多一条边到达的 dfn 最小的点就是 \(x\) 自己,说明没有孙子通过一条边跳过你爷爷 \(x\) 去更上面的点。具体的,如果存在 \(low_v=dfn_x\),其中 \(v\) 是 \(x\) 的儿子,则说明 \(x\) 是割点(\(x\) 为根则至少两个这样的儿子),我们找到了一个点双联通分量。
那么在建立圆方树的过程中,我们维护一个栈来记录当前有那些点还未确定所属点双,找到点双后就一直弹栈直到 \(v\) 被弹出,这些点都和新建的方点连边。
下面有一份求点双的模板代码(G 表示原图,T 是新建的圆方树)
\(\bigstar\texttt{Important}\):别忘了最后将 \(x\) 自己也和方点连边。
void tarjan(int u)
{
dfn[u]=low[u]=++Time,sta[++tp]=u;
for(int v:G[u])
{
if(!dfn[v])
{
tarjan(v),low[u]=min(low[u],low[v]);
if(low[v]==dfn[u])
{
int hav=0; ++All;
for(int x=0;x!=v;tp--) x=sta[tp],T[x].pb(All),T[All].pb(x),hav++;
T[u].pb(All),T[All].pb(u),;
siz[All]=++hav;
}
}
else low[u]=min(low[u],dfn[v]);
}
}
3 圆方树的应用
3.1 [APIO2018] 铁人两项
给定一张无向图,询问点对 \((s,x,t)\) 的数量,满足存在一条路径 \(s\rightarrow x\rightarrow t\) 经过路径上的点有且仅有一次。
\(n\le 10^5,m\le 2\times 10^5\)。
如果确定 \(s,t\),那么他们之间选择 \(x\) 的方案数就是所有 \(s\) 到 \(t\) 路径上点的并。
利用点双的性质,对于任意点双中的不同的点 \(s,t\),一定存在一条路径 \(s\rightarrow x\rightarrow t\) 只经过路径上的点一次(证明详见粉兔的网络流证法),我们需要求的其实就是 \(s\rightarrow t\) 经过的所有点双的并。
那么将题目转化到圆方树上,设方点的权值为点双的大小,圆点的权值为 \(-1\),\(s\rightarrow t\) 的方案数就是路径上的权值之和,一遍 dfs 即可。
3.2 CF487E Tourists
给定一张无向图,有两种操作:
- 修改一个点的点权;
- 查询 \(s\) 到 \(t\) 的所有简单路径上的点权的最小值。
\(n,m,q\le 10^5\)。
首先有个暴力的做法,修改一个源点的点权的时候暴力更改所有与它相邻的方点的点权(方点点权为相邻圆点点权的最小值),答案为圆方树上路径最小值。
当然,这样会被一行菊花图卡掉,但是!圆方树上圆点与方点是交错的!
也就是说,在更改一个圆点的点权的时候,会更改所有儿子方点的点权和一个父亲方点的点权,查询方点的点权就等于查询所有儿子圆点点权和一个父亲圆点点权的最小值,我们完全可以将修改改为“更改父亲方点点权”,查询时,如果 \(s\) 到 \(t\) 路径的 \(lca\) 是方点,再算入 \(lca\) 的父亲的点权。
具体实现在每个方点记录一个 multiset 维护儿子圆点的权值,查询路径最小值用树剖。
3.3 [SDOI2018]战略游戏
嘴了嘴了,建圆方树,可以 \(\mathcal{O(n)}\) 统计答案。如果多次询问,每次建立虚树即可。


