玩转线段树(扫描线、优化建图、线段树分治……)
线段树模板
(远古代码了,还在用指针)
注意 \(pushdown\) 操作的优先级:
儿子的值 \(=\) 此刻儿子的值 \(\times\) 爸爸的乘法 \(lazy~+\) 儿子的区间长度 \(\times\) 爸爸的加法 \(lazy\)
即:先下传 \(lazymul\) ,再下传 \(lazyadd\) 。
$\texttt{code}$
struct Tree
{
int sum,add,mul;
}tree[Maxn*4];
void pushdown(int p,int nl,int nr)
{
if(nl==nr) return;
int mid=(nl+nr)>>1,tmpm=tree[p].mul,tmpa=tree[p].add,ls=p<<1,rs=p<<1|1;
tree[ls].add=1ll*tree[ls].add*tmpm%mod,tree[rs].add=1ll*tree[rs].add*tmpm%mod;
tree[ls].mul=1ll*tree[ls].mul*tmpm%mod,tree[rs].mul=1ll*tree[rs].mul*tmpm%mod;
tree[ls].sum=1ll*tree[ls].sum*tmpm%mod,tree[rs].sum=1ll*tree[rs].sum*tmpm%mod;
tree[ls].sum=(tree[ls].sum+1ll*(mid-nl+1ll)*tmpa)%mod;
tree[rs].sum=(tree[rs].sum+1ll*(nr-mid)*tmpa)%mod;
tree[ls].add=(tree[ls].add+tmpa)%mod,tree[rs].add=(tree[rs].add+tmpa)%mod;
tree[p].add=0,tree[p].mul=1;
}
void add(int p,int nl,int nr,int l,int r,int k)
{
if(nl>=l && nr<=r)
{
tree[p].sum=(tree[p].sum+1ll*k*(nr-nl+1ll))%mod;
tree[p].add=(tree[p].add+k)%mod;
return;
}
pushdown(p,nl,nr);
int mid=(nl+nr)>>1;
if(mid>=l) add(p<<1,nl,mid,l,r,k);
if(mid<r) add(p<<1|1,mid+1,nr,l,r,k);
tree[p].sum=(tree[p<<1].sum+tree[p<<1|1].sum)%mod;
}
void mul(int p,int nl,int nr,int l,int r,int k)
{
if(nl>=l && nr<=r)
{
tree[p].mul=1ll*tree[p].mul*k%mod;
tree[p].add=1ll*tree[p].add*k%mod;
tree[p].sum=1ll*tree[p].sum*k%mod;
return;
}
pushdown(p,nl,nr);
int mid=(nl+nr)>>1;
if(mid>=l) mul(p<<1,nl,mid,l,r,k);
if(mid<r) mul(p<<1|1,mid+1,nr,l,r,k);
tree[p].sum=(tree[p<<1].sum+tree[p<<1|1].sum)%mod;
}
扫描线
线段树的应用 。
关于扫描线为什么不用 \(pushdown\) 操作:
这题如果一个结点在 覆盖这个区间时下传了标记 ,整棵子树都被覆盖一次,取消覆盖时要遍历整棵子树重新获取信息 。
$\texttt{solution}$
大致步骤:
-
先进行离散化处理 。
-
处理矩形的上下边界,变为一条条扫描线 。
-
进行区间加操作 。
每个区间( 线段树上的点 )记录信息:
-
有多少条线段 直接 将这条线段全部覆盖( 从父亲那里继承来的不能算 ) 。
-
这个区间内被矩形覆盖到的实际宽度之和 。
注意:
-
进行区间加操作时的下标是离散化后的下标,而统计的答案是实际大小 。
-
空间限制宽泛,当算不清楚到底要开多大时尽量往打了开 。
大致过程如图所示:

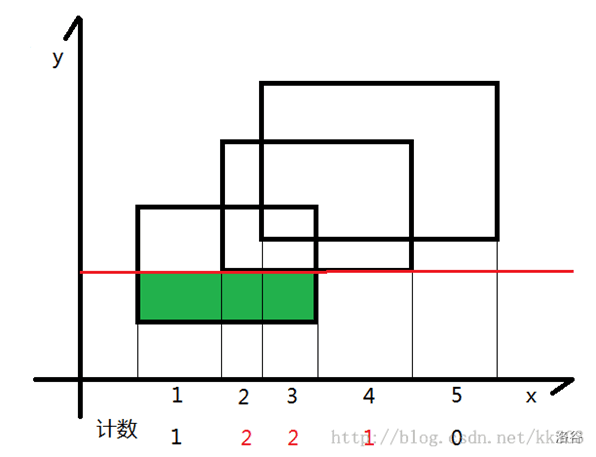


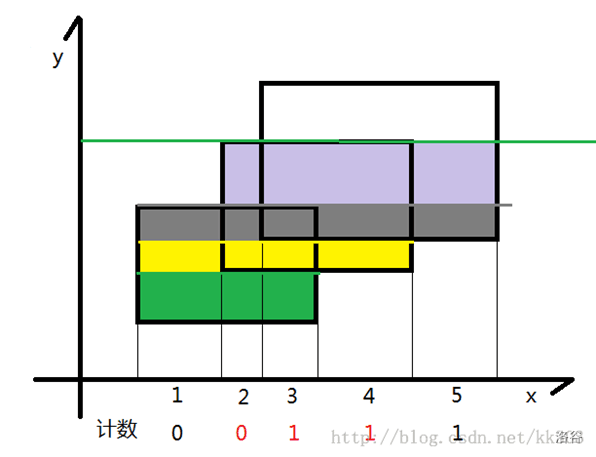
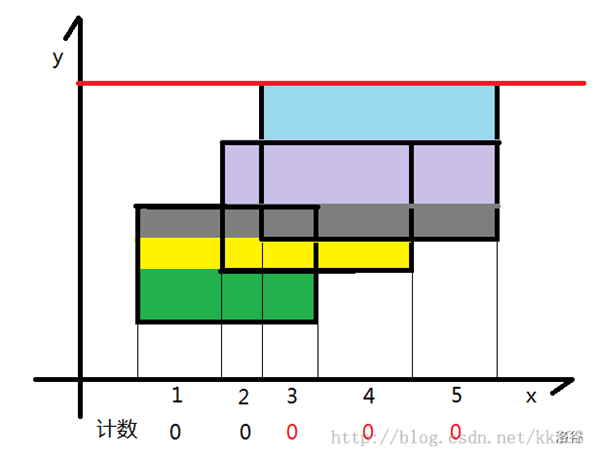
$\texttt{code}$
#include<bits/stdc++.h>
using namespace std;
#define Maxn 200005
typedef long long ll;
ll n,tot,l,r,ans,cnt;
ll X[Maxn][2],Y[Maxn][2],True[Maxn*2];
struct Dis { ll num,val; } tmp[Maxn*2];
struct Seg { ll xl,xr,h,val; } seg[Maxn*2];
struct Tree
{
ll sum;
ll Lazy;
}tree[Maxn*8];
bool cmp1(Dis x,Dis y) { return x.val<y.val; }
bool cmp2(Seg x,Seg y) { return x.h<y.h; }
void pushup(ll p,ll nl,ll nr)
{
if(tree[p].Lazy) tree[p].sum=True[nr+1]-True[nl];
else tree[p].sum=tree[p<<1].sum+tree[p<<1|1].sum;
}
void add(ll p,ll nl,ll nr,ll k)
{
if(nl>=l && nr<=r)
{
tree[p].Lazy+=k;
pushup(p,nl,nr);
return;
}
ll mid=(nl+nr)>>1;
if(mid>=l) add(p<<1,nl,mid,k);
if(mid<r) add(p<<1|1,mid+1,nr,k);
pushup(p,nl,nr);
}
int main()
{
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
scanf("%lld",&n);
for(ll i=1;i<=n;i++) scanf("%lld%lld%lld%lld",&X[i][0],&Y[i][0],&X[i][1],&Y[i][1]);
for(ll i=1;i<=n;i++) tmp[i*2-1]=(Dis){i*2-1,X[i][1]},tmp[i*2]=(Dis){i*2,X[i][0]};
sort(tmp+1,tmp+n*2+1,cmp1);
tmp[0].val=-1;
for(ll i=1;i<=n*2;i++)
{
if(tmp[i].val!=tmp[i-1].val) True[++cnt]=tmp[i].val;
X[(tmp[i].num+1)/2][tmp[i].num%2]=cnt;
} // 离散化
for(ll i=1;i<=n;i++)
seg[++tot]=(Seg){X[i][0],X[i][1],Y[i][0],1},
seg[++tot]=(Seg){X[i][0],X[i][1],Y[i][1],-1};
sort(seg+1,seg+tot+1,cmp2); // 以上是预处理部分
for(ll i=1;i<=tot;i++)
{
ans=ans+1ll*(seg[i].h-seg[i-1].h)*tree[1].sum;
l=seg[i].xl,r=seg[i].xr-1;
add(1,1,cnt,seg[i].val);
}
printf("%lld\n",ans);
//fclose(stdin);
//fclose(stdout);
return 0;
}
$\texttt{solution}$
其他部分与扫描线模板一样,就是统计的时候记录这个区间被分为多少个不相交的线段,另外进行两次扫描线( 横着一次,竖着一次 ) 。
如何记录被分为多少个线段:
-
记录的值:( 一条线段 \([l,r]\) 实际表示 \([True_l,True_{r+1}-1]\) ,这同扫描线模板一样 )
-
\(tag\) : 整个区间被整体覆盖了几次( 不下传 )
-
\(sum\) : 整个区间被几条互不相交的线段覆盖
-
\(Coverl\) : 左端点是否被覆盖( 合并用 )
-
\(Coverr\) : 右端点是否被覆盖( 合并用 )
-
-
\(pushup\) 操作
$\texttt{code}$
#include<bits/stdc++.h>
using namespace std;
#define infll 0x7f7f7f7f7f7f7f7f
#define inf 0x7f7f7f7f
#define Maxn 40005
typedef long long ll; // 习惯性开大空间
ll maxll(ll x,ll y){ return x>y?x:y; }
ll minll(ll x,ll y){ return x<y?x:y; }
int n,l,r,cntx,cnty,tot;
int Truex[Maxn*2],Truey[Maxn*2],X[Maxn][2],Y[Maxn][2];
ll ans=0;
struct Dis { int num,val; } Inx[Maxn*2],Iny[Maxn*2];
struct Seg { int nl,nr,h,val; } segx[Maxn*2],segy[Maxn*2];
bool cmp1(Dis x,Dis y){ return x.val<y.val; }
bool cmp2(Seg x,Seg y){ return x.h<y.h; }
struct Tree
{
int sum,tag,Coverl,Coverr;
}tree[Maxn*16];
void workpre()
{
scanf("%d",&n),tot=n*2;
for(int i=1;i<=n;i++) scanf("%d%d%d%d",&X[i][0],&Y[i][0],&X[i][1],&Y[i][1]);
for(int i=1;i<=n;i++) Inx[i*2-1]=(Dis){i*2-1,X[i][1]},Inx[i*2]=(Dis){i*2,X[i][0]};
for(int i=1;i<=n;i++) Iny[i*2-1]=(Dis){i*2-1,Y[i][1]},Iny[i*2]=(Dis){i*2,Y[i][0]};
sort(Inx+1,Inx+tot+1,cmp1),sort(Iny+1,Iny+tot+1,cmp1);
Inx[0].val=Iny[0].val=-inf;
for(int i=1;i<=tot;i++)
{
if(Inx[i].val!=Inx[i-1].val) Truex[++cntx]=Inx[i].val;
if(Iny[i].val!=Iny[i-1].val) Truey[++cnty]=Iny[i].val;
X[(Inx[i].num+1)/2][Inx[i].num%2]=cntx;
Y[(Iny[i].num+1)/2][Iny[i].num%2]=cnty;
}
for(int i=1;i<=n;i++)
{
segx[i*2-1]=(Seg){X[i][0],X[i][1],Y[i][0],1};
segx[i*2]=(Seg){X[i][0],X[i][1],Y[i][1],-1};
segy[i*2-1]=(Seg){Y[i][0],Y[i][1],X[i][0],1};
segy[i*2]=(Seg){Y[i][0],Y[i][1],X[i][1],-1};
}
sort(segx+1,segx+tot+1,cmp2),sort(segy+1,segy+tot+1,cmp2);
}
void build(int p,int nl,int nr)
{
tree[p].sum=tree[p].tag=tree[p].Coverl=tree[p].Coverr=0;
if(nl==nr) return;
int mid=(nl+nr)>>1;
build(p<<1,nl,mid),build(p<<1|1,mid+1,nr);
}
void pushup(int p,int nl,int nr)
{
if(tree[p].tag) tree[p].sum=tree[p].Coverl=tree[p].Coverr=1;
else if(nl==nr) tree[p].sum=tree[p].Coverl=tree[p].Coverr=0;
else
{
tree[p].sum=tree[p<<1].sum+tree[p<<1|1].sum;
if(tree[p<<1].Coverr && tree[p<<1|1].Coverl) tree[p].sum--;
tree[p].Coverl=tree[p<<1].Coverl;
tree[p].Coverr=tree[p<<1|1].Coverr;
}
}
void add(int p,int nl,int nr,int k)
{
if(nl>=l && nr<=r)
{
tree[p].tag+=k;
pushup(p,nl,nr);
return;
}
int mid=(nl+nr)>>1;
if(mid>=l) add(p<<1,nl,mid,k);
if(mid<r) add(p<<1|1,mid+1,nr,k);
pushup(p,nl,nr);
}
int main()
{
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
workpre(); // 输入 + 初始化
for(int i=1;i<tot;i++)
{
l=segx[i].nl,r=segx[i].nr-1;
add(1,1,cntx,segx[i].val);
ans+=2ll*tree[1].sum*(Truey[segx[i+1].h]-Truey[segx[i].h]);
}
build(1,1,cnty);
for(int i=1;i<tot;i++)
{
l=segy[i].nl,r=segy[i].nr-1;
add(1,1,cnty,segy[i].val);
ans+=2ll*tree[1].sum*(Truex[segy[i+1].h]-Truex[segy[i].h]);
}
printf("%lld\n",ans);
//fclose(stdin);
//fclose(stdout);
return 0;
}
区间最长的 XX
比如最长的由 \(0\) 组成的子串。
可以在每一个节点存储:
-
从区间最左端开始的最长子串
-
从区间最右端开始的最长子串
-
整个区间的最长子串
合并时参考代码 。
例题:
struct Tree
{
int ml,mr,ans;
}tree[Maxn<<2];
void pushup(int p,int nl,int nr)
{
int mid=(nl+nr)>>1;
tree[p].ml=tree[p<<1].ml,tree[p].mr=tree[p<<1|1].mr;
if(tree[p<<1].ml==mid-nl+1) tree[p].ml=tree[p<<1].ml+tree[p<<1|1].ml;
if(tree[p<<1|1].mr==nr-mid) tree[p].mr=tree[p<<1].mr+tree[p<<1|1].mr;
tree[p].ans=max(max(tree[p<<1].ans,tree[p<<1|1].ans),tree[p<<1].mr+tree[p<<1|1].ml);
}
void build(int p,int nl,int nr)
{
if(nl==nr) { tree[p].ml=tree[p].mr=tree[p].ans=1; return; }
int mid=(nl+nr)>>1;
if(mid>=nl) build(p<<1,nl,mid);
if(mid<nr) build(p<<1|1,mid+1,nr);
pushup(p,nl,nr);
}
线段树优化建图
CF786B Legacy
描述:有 \(n(n\le 10^5)\) 个点,每次给出一些边 u->v,u->[l,r],[l,r]->v,求出 \(s\) 到 \(t\) 的最短路。
由于 \(n\) 超级大,\(n^2\) 建图肯定会 T,因此有了线段树优化建图。
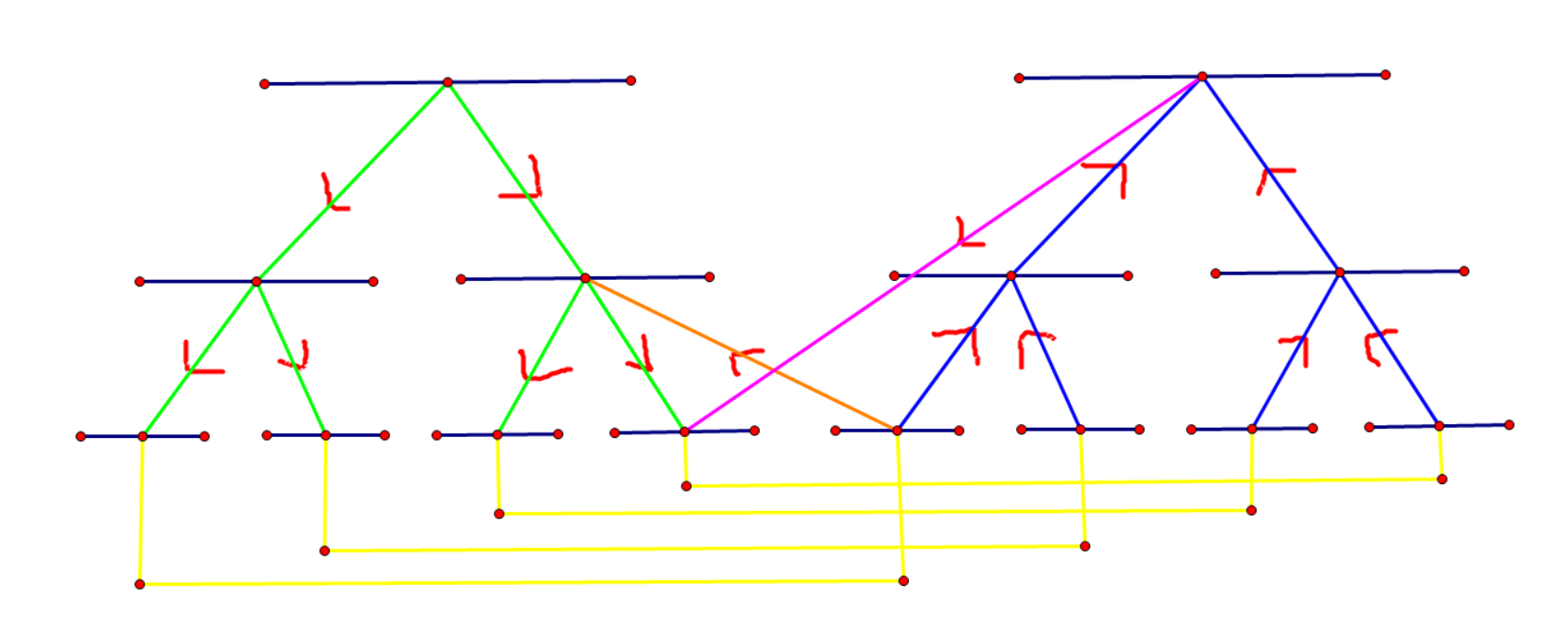
(感谢 tzc_wk 制作的图片)
我们将区间放在线段树上,即 out 树和 in 树,分别表示两种连边操作,将每个区间分为不超过 \(\log n\) 个小区间,分别建立虚点并连边。
注意在两棵树的底层每对点之间都连上了长度为 \(0\) 的边,不然这个路径只会经过一条边。
我们在 id 与 id 之间连边,千万不能用线段树的下标来处理!!
特别注意——关于空间:由于线段树的一系列操作,所有点都需要开到至少 $4\times $【树的个数】倍大小,而边数一棵树就需要 \(4\) 被空间,加上后来连上的一些边,需要开到 \(32\) 至 \(64\) 倍。
CF786B 模板代码
// Author:A weak man named EricQian
#include<bits/stdc++.h>
using namespace std;
#define infll 0x7f7f7f7f7f7f7f7f
#define inf 0x3f3f3f3f
#define Maxn 100005 // 空间应该开多大?
#define pa pair<ll,int>
#define fi first
#define se second
typedef long long ll;
inline int rd()
{
int x=0;
char ch,t=0;
while(!isdigit(ch = getchar())) t|=ch=='-';
while(isdigit(ch)) x=x*10+(ch^48),ch=getchar();
return x=t?-x:x;
}
inline ll maxll(ll x,ll y){ return x>y?x:y; }
inline ll minll(ll x,ll y){ return x<y?x:y; }
inline ll absll(ll x){ return x>0ll?x:-x; }
inline ll gcd(ll x,ll y){ return (y==0)?x:gcd(y,x%y); }
int n,q,s,id,tot;
int hea[Maxn<<3],nex[Maxn<<5],ver[Maxn<<5];
int indot[Maxn<<3],outdot[Maxn<<3],numin[Maxn<<3],numout[Maxn<<3];
ll ds[Maxn<<3],edg[Maxn<<5];
bool vis[Maxn<<3];
inline void add_edge(int x,int y,ll d){ ver[++tot]=y,nex[tot]=hea[x],hea[x]=tot,edg[tot]=d; }
void build(int p,int nl,int nr)
{
if(nl==nr) { numout[p]=nl,numin[p]=nl+n; return; }
numout[p]=++id,numin[p]=++id;
int mid=(nl+nr)>>1;
build(p<<1,nl,mid),build(p<<1|1,mid+1,nr);
add_edge(numout[p<<1],numout[p],0),add_edge(numout[p<<1|1],numout[p],0);
add_edge(numin[p],numin[p<<1],0),add_edge(numin[p],numin[p<<1|1],0);
}
void add_out_tree(int p,int nl,int nr,int l,int r,int x,int w)
{
if(nl>=l && nr<=r) { add_edge(numout[p],x,w); return; }
int mid=(nl+nr)>>1;
if(mid>=l) add_out_tree(p<<1,nl,mid,l,r,x,w);
if(mid<r) add_out_tree(p<<1|1,mid+1,nr,l,r,x,w);
}
void add_in_tree(int p,int nl,int nr,int l,int r,int x,int w)
{
if(nl>=l && nr<=r) { add_edge(x,numin[p],w); return; }
int mid=(nl+nr)>>1;
if(mid>=l) add_in_tree(p<<1,nl,mid,l,r,x,w);
if(mid<r) add_in_tree(p<<1|1,mid+1,nr,l,r,x,w);
}
inline void dij()
{
priority_queue<pa> q;
for(int i=1;i<=id;i++) ds[i]=infll;
ds[s]=0,q.push(pa(0,s));
while(!q.empty())
{
int cur=q.top().se; q.pop();
if(vis[cur]) continue;
vis[cur]=true;
for(int i=hea[cur];i;i=nex[i]) if(ds[ver[i]]>ds[cur]+edg[i])
ds[ver[i]]=ds[cur]+edg[i],q.push(pa(-ds[ver[i]],ver[i]));
}
}
int main()
{
//ios::sync_with_stdio(false); cin.tie(0);
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
n=rd(),q=rd(),s=rd(),id=n*2,build(1,1,n);
for(int i=1;i<=n;i++) outdot[i]=i;
for(int i=1;i<=n;i++) indot[i]=i+n; // 记得最终答案在 i+n
for(int i=1;i<=n;i++) add_edge(i+n,i,0),add_edge(i,i+n,0);
// out -> in
for(int i=1,opt,x,l,r,w;i<=q;i++)
{
opt=rd();
if(opt==1) l=rd(),r=rd(),w=rd(),add_edge(outdot[l],outdot[r],w);
else if(opt==2) x=rd(),l=rd(),r=rd(),w=rd(),add_in_tree(1,1,n,l,r,x,w);
else x=rd(),l=rd(),r=rd(),w=rd(),add_out_tree(1,1,n,l,r,x+n,w);
}
dij();
for(int i=1;i<=n;i++) printf("%lld%c",(ds[i+n]==infll)?-1:ds[i+n],(i==n)?'\n':' ');
//fclose(stdin);
//fclose(stdout);
return 0;
}
P3588 [POI2015] PUS
题意:给定长度为 \(n\) 的序列,其中有若干个点已经有了权值,其他没有。又有 \(m\) 个区间,要求区间内选择的 \(k_i\) 个点的权值严格大于其他 \(len-k\) 个点,要求输出一种合法的方案,或者判定不可能实现。
困难的是要求区间内选择了 \(k_i\) 个点,而这些点将整个区间分为了若干段。
考虑对于每个区间建立一个新的点,从每个子区间向这个点连边,并从这个点向选中的每一个点连边。
从 out 树出发,用拓扑排序可以求出每一个点的最小权值。而如果不能完成拓扑,则表明不合法。
$\texttt{code}$
// Author:A weak man named EricQian
#include<bits/stdc++.h>
using namespace std;
#define infll 0x7f7f7f7f7f7f7f7f
#define inf 0x3f3f3f3f
#define Maxn 10000005
typedef long long ll;
inline int rd()
{
int x=0;
char ch,t=0;
while(!isdigit(ch = getchar())) t|=ch=='-';
while(isdigit(ch)) x=x*10+(ch^48),ch=getchar();
return x=t?-x:x;
}
inline ll maxll(ll x,ll y){ return x>y?x:y; }
inline ll minll(ll x,ll y){ return x<y?x:y; }
inline ll absll(ll x){ return x>0ll?x:-x; }
inline ll gcd(ll x,ll y){ return (y==0)?x:gcd(y,x%y); }
int n,s,m,id,tot;
int hea[Maxn],nex[Maxn],ver[Maxn],edg[Maxn];
int ind[Maxn],num[Maxn],r[Maxn],ds[Maxn];
inline void add_edge(int x,int y,int d){ ver[++tot]=y,nex[tot]=hea[x],hea[x]=tot,edg[tot]=d,ind[y]++; }
void build(int p,int nl,int nr)
{
if(nl==nr) { num[p]=nl; return; }
num[p]=++id;
int mid=(nl+nr)>>1;
build(p<<1,nl,mid),build(p<<1|1,mid+1,nr);
add_edge(num[p<<1],num[p],0),add_edge(num[p<<1|1],num[p],0);
}
void change(int p,int nl,int nr,int l,int r,int x)
{
if(nl>=l && nr<=r) { add_edge(num[p],x,0); return; }
int mid=(nl+nr)>>1;
if(mid>=l) change(p<<1,nl,mid,l,r,x);
if(mid<r) change(p<<1|1,mid+1,nr,l,r,x);
}
bool topo()
{
queue<int> q;
for(int i=1;i<=id;i++) if(!ind[i]) q.push(i);
for(int i=1;i<=id;i++) ds[i]=max(ds[i],1);
while(!q.empty())
{
int cur=q.front(); q.pop();
for(int i=hea[cur];i;i=nex[i])
{
ds[ver[i]]=max(ds[ver[i]],ds[cur]+edg[i]);
if(r[ver[i]] && r[ver[i]]>ds[ver[i]]) return false;
ind[ver[i]]--;
if(!ind[ver[i]]) q.push(ver[i]);
}
}
for(int i=1;i<=id;i++) if(ind[i] || ds[i]>1000000000) return false;
return true;
}
int main()
{
//ios::sync_with_stdio(false); cin.tie(0);
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
id=n=rd(),s=rd(),m=rd();
for(int i=1,p,d;i<=s;i++) p=rd(),d=rd(),r[p]=ds[p]=d;
build(1,1,n);
for(int i=1,l,r,k,Last;i<=m;i++)
{
Last=l=rd(),r=rd(),k=rd(),id++;
for(int j=1,pos;j<=k;j++)
{
pos=rd(),add_edge(id,pos,1);
if(pos>Last) change(1,1,n,Last,pos-1,id);
Last=pos+1;
}
if(Last<=r) change(1,1,n,Last,r,id);
}
if(topo()) { printf("TAK\n"); for(int i=1;i<=n;i++) printf("%d ",ds[i]); printf("\n"); }
else printf("NIE\n");
//fclose(stdin);
//fclose(stdout);
return 0;
}
P5025 [SNOI2017]炸弹
在一条直线上有 \(n\) 个炸弹,每个炸弹的坐标是 \(x_i\),爆炸半径是 \(r_i\),当一个炸弹爆炸时,如果另一个炸弹所在位置 \(x_j\) 满足: \(|x_j-x_i| \le r_i\),那么,该炸弹也会被引爆。
现在,请你帮忙计算一下,先把第 \(i\) 个炸弹引爆,将引爆多少个炸弹呢?
我们先进行普通的线段树优化建图,之后需要求出每个点能够到达的【叶子节点的个数】。
与其统计叶子节点,不如想方法记录下每个点最远能扩展到的最左端、最右端的炸弹编号。
容易想到用强联通分量解决问题。
我们对于这张图跑强联通分量,使图变为一张 DAG。
在 DAG 上我们可以暴力(相当于 dp)求出每个连通块能够到达的最远点,最终输出方案即可。
$\texttt{code}$
// Author:A weak man named EricQian
#include<bits/stdc++.h>
using namespace std;
#define infll 0x7f7f7f7f7f7f7f7f
#define inf 0x3f3f3f3f
#define Maxn 500005 // 空间!!!
#define pb push_back
#define mod 1000000007
typedef long long ll;
inline ll rd()
{
ll x=0;
char ch,t=0;
while(!isdigit(ch = getchar())) t|=ch=='-';
while(isdigit(ch)) x=x*10+(ch^48),ch=getchar();
return x=t?-x:x;
}
int n,id,tot,sum,Time,tp,ans;
ll x[Maxn],d[Maxn];
int hea[Maxn<<2],nex[Maxn<<4],ver[Maxn<<4];
int dfn[Maxn<<2],low[Maxn<<2],sta[Maxn<<2],bel[Maxn<<2];
bool ins[Maxn<<2],vis[Maxn<<2];
int tol[Maxn<<2],tor[Maxn<<2],num[Maxn<<2];
int L[Maxn<<2],R[Maxn<<2];
vector<int> g[Maxn<<2];
inline void add_edge(int x,int y){ ver[++tot]=y,nex[tot]=hea[x],hea[x]=tot; }
// 由于只用建立一棵树,所以将连出节点与连入节点合并。
// 选择从上往下连边
void build(int p,int nl,int nr)
{
if(nl==nr) { num[p]=nl; return; }
int mid=(nl+nr)>>1;
build(p<<1,nl,mid),build(p<<1|1,mid+1,nr);
num[p]=++id;
tol[id]=min(tol[num[p<<1]],tol[num[p<<1|1]]);
tor[id]=max(tor[num[p<<1]],tor[num[p<<1|1]]);
add_edge(num[p],num[p<<1]),add_edge(num[p],num[p<<1|1]);
}
void change(int p,int nl,int nr,int l,int r,int x)
{
if(nl>=l && nr<=r) { add_edge(x,num[p]); return; }
int mid=(nl+nr)>>1;
if(mid>=l) change(p<<1,nl,mid,l,r,x);
if(mid<r) change(p<<1|1,mid+1,nr,l,r,x);
}
void tarjan(int x)
{
dfn[x]=low[x]=++Time,sta[++tp]=x,ins[x]=true;
for(int i=hea[x];i;i=nex[i])
{
if(!dfn[ver[i]]) tarjan(ver[i]),low[x]=min(low[x],low[ver[i]]);
else if(ins[ver[i]]) low[x]=min(low[x],dfn[ver[i]]);
}
if(dfn[x]==low[x])
{
sum++,L[sum]=inf;
do
{
x=sta[tp--],ins[x]=false,bel[x]=sum,
L[sum]=min(L[sum],tol[x]),R[sum]=max(R[sum],tor[x]);
}while(dfn[x]!=low[x]);
}
}
void Find(int x)
{
vis[x]=true;
for(int v:g[x])
{
if(vis[v]) L[x]=min(L[x],L[v]),R[x]=max(R[x],R[v]);
else Find(v),L[x]=min(L[x],L[v]),R[x]=max(R[x],R[v]);
}
}
int main()
{
id=n=rd(),x[n+1]=infll;
for(int i=1;i<=n;i++) x[i]=rd(),d[i]=rd();
for(int i=1;i<=n;i++)
tol[i]=lower_bound(x+1,x+n+1,x[i]-d[i])-x,
tor[i]=upper_bound(x+1,x+n+1,x[i]+d[i])-x-1;
build(1,1,n);
for(int i=1;i<=n;i++) change(1,1,n,tol[i],tor[i],i);
for(int i=1;i<=id;i++) if(!dfn[i]) tarjan(i);
for(int i=1;i<=id;i++) for(int j=hea[i];j;j=nex[j])
if(bel[i]!=bel[ver[j]]) g[bel[i]].pb(bel[ver[j]]);
for(int i=1;i<=sum;i++) if(!vis[i]) Find(i);
for(int i=1;i<=n;i++)
ans=(ans+1ll*i*(R[bel[i]]-L[bel[i]]+1)%mod)%mod;
printf("%d\n",ans);
return 0;
}
线段树分治(按时间分治)
\(\color{yellow}{\bigstar\texttt{Attention-1}}\):记得删边操作的结束 id 是 \(i-1\) 而不是 \(i\)!!!
\(\color{yellow}{\bigstar\texttt{Attention-2}}\):在加入信息的时候记得判断 \(pl\le pr\)!!!
\(\color{yellow}{\bigstar\texttt{Attention-3}}\):线段树会把线段拆到小端点上去,由于结束 id \(i-1\) 的影响,可能在线段树端点上会同时存在修改和询问操作。
P5787 二分图 /【模板】线段树分治
就是将每个操作放到线段树上,是的最终处理次数不超过 \(n\log n\) 次,从而优化复杂度。
这一题是常见的维护并查集操作,并不能使用路径压缩,而是启发式合并。
当我们进入一个时间段的时候,将这个点加入一个栈,并连边。
当我们要走回祖先时,再将栈中的东西弹出,使这个点的操作全部被撤回。
$\texttt{code}$
// Author:A weak man named EricQian
#include<bits/stdc++.h>
using namespace std;
#define infll 0x7f7f7f7f7f7f7f7f
#define inf 0x3f3f3f3f
#define Maxn 100005
#define pb push_back
#define pa pair<int,int>
#define fi first
#define se second
typedef long long ll;
inline int rd()
{
int x=0;
char ch,t=0;
while(!isdigit(ch = getchar())) t|=ch=='-';
while(isdigit(ch)) x=x*10+(ch^48),ch=getchar();
return x=t?-x:x;
}
inline ll maxll(ll x,ll y){ return x>y?x:y; }
inline ll minll(ll x,ll y){ return x<y?x:y; }
inline ll absll(ll x){ return x>0ll?x:-x; }
inline ll gcd(ll x,ll y){ return (y==0)?x:gcd(y,x%y); }
int n,m,k,tp;
int fa[Maxn<<1],siz[Maxn<<1];
pa sta[Maxn<<2];
vector<pa> g[Maxn<<2];
int Find(int x){ return (fa[x]==x)?x:Find(fa[x]); }
void Insert(int p,int nl,int nr,int l,int r,int x,int y)
{
if(nl>=l && nr<=r) { g[p].pb(pa(x,y)); return; }
int mid=(nl+nr)>>1;
if(mid>=l) Insert(p<<1,nl,mid,l,r,x,y);
if(mid<r) Insert(p<<1|1,mid+1,nr,l,r,x,y);
}
inline void merge(int x,int y)
{
// printf("merge(%d %d) ",x,y);
x=Find(x),y=Find(y);
if(x==y) return;
// printf("fa : %d %d\n",x,y);
if(siz[x]>siz[y]) swap(x,y);
sta[++tp]=pa(x,y);
fa[x]=y,siz[y]+=siz[x];
}
inline void del(int x,int y)
{
fa[x]=x,siz[y]-=siz[x];
}
void update(int p,int nl,int nr)
{
int Lasttop=tp,opt=1;
for(int i=0;i<g[p].size();i++)
{
if(Find(g[p][i].fi)==Find(g[p][i].se))
{
for(int j=nl;j<=nr;j++) printf("No\n");
opt=0;
break;
}
merge(g[p][i].fi,g[p][i].se+n);
merge(g[p][i].fi+n,g[p][i].se);
}
if(opt)
{
if(nl==nr) printf("Yes\n");
else
{
int mid=(nl+nr)>>1;
update(p<<1,nl,mid),update(p<<1|1,mid+1,nr);
}
}
while(tp>Lasttop) del(sta[tp].fi,sta[tp].se),tp--;
}
int main()
{
//ios::sync_with_stdio(false); cin.tie(0);
freopen("9.in","r",stdin);
freopen("my.out","w",stdout);
n=rd(),m=rd(),k=rd();
for(int i=1;i<=n+n;i++) fa[i]=i,siz[i]=1;
for(int i=1,x,y,l,r;i<=m;i++)
{
x=rd(),y=rd(),l=rd(),r=rd();
if(l<r) Insert(1,1,k,l+1,r,x,y);
}
update(1,1,k);
//fclose(stdin);
//fclose(stdout);
return 0;
}
模板题 P5227 [AHOI2013]连通图。
CF1140F Extending Set of Points
题意:给定一个直角坐标系,有若干个点 \((x_i,y_i)\) 会在 \([l_i,r_i]\) 时间内出现。定义一个图的张集为 \(S\),若干 \((x_1,y_1),(x_1,y_2),(x_2,y_1)\) 都在这个集合中,那么 \((x_2,y_2)\) 也在这个集合中。对于每个时刻,求出张集大小。
只要将行和列拆开考虑,其实操作是一样一样的。
发现如果将一个点 \((x,y)\) 看做有 \(x\rightarrow (y+n)\) 的一条无向边,显然会形成一张二分图。
那么最终产生的张集一定是每个连通的二分图中,一边的点数乘上另一边的点数,因此像上一题一样维护并查集就可以了。
CF576E Painting Edges,CF603E Pastoral Oddities
这两道题都没有给定每条边是否加入,需要在线段树分治的过程中做出决策。
第一题我们采用的方法是将这条边当前加入到一定会影响的区间(到下一次修改这条边之前),每次查看能否加入这条边后,选择继续添加上一条边还是使用新的边。
第二题发现答案递减,需要找出每条边的结束位置,可以选择在倒序分治的过程中依次枚举每条边进行决策。
这样可以类似在线地处理这些询问。
还有其他的例题,如 P4585 [FJOI2015]火星商店问题(和可持久化 Trie 结合)用了平衡复杂度的思想,P3767 膜法还没补。
Segment Tree Beats
引用自djwj233 的博客——Segment Tree Beats 学习笔记。
Segment Tree Beats,又称吉司机线段树,是一种可以维护对区间取 \(\min\),\(\max\) 的操作的线段树数据结构。
它还可以维护区间历史最大值、区间历史最小值等。
一般的区间历史最大值
先从P4314 CPU 监控下手,需要维护区间加、减、赋值、询问区间最大值、询问历史最大值。
仿照一般的区间询问,我们记录一套 tag,用 add,hadd,cov,hcov,分别表示当前整体区间加、在这一段操作序列中最大区间加、整体覆盖、这一段操作序列中最大覆盖。
其中,操作序列定义为这段时间内对某一个区间整体操作的操作集合。当我们需要 pushdown 并操作子区间时,应当清空操作序列并将原来的操作序列放到子区间上去。
也就是说,pushdown 的本质是将父亲的操作序列接到子节点上并清空父亲的操作序列。
关于如何处理这道题的操作序列,可以这么做:
-
如果没有整体赋值操作,用 add 和 hadd 记下整体加减的最终值与最大值。
-
如果有整体赋值操作,清空以前的 add(记得保存 hadd)后开始记覆盖与覆盖最大值,在这种情况下,所有的“加”操作都可以转化为“覆盖”操作。
$\texttt{code}$
void cover(int p,int x,int hx)
{
// if(tree[p].cov==inf)
// tree[p].hmx=max(tree[p].hmx,tree[p].mx+tree[p].hadd);
tree[p].hcov=max(tree[p].hcov,hx);
tree[p].hmx=max(tree[p].hmx,tree[p].hcov);
tree[p].mx=x,tree[p].cov=x;
tree[p].add/*=tree[p].hadd*/=0;
}
void add(int p,int x,int hx)
{
tree[p].hadd=max(tree[p].hadd,tree[p].add+hx);
tree[p].hmx=max(tree[p].hmx,tree[p].mx+hx);
tree[p].add+=x,tree[p].mx+=x;
}
void change(int p,int x,int hx)
{
if(tree[p].cov==inf) add(p,x,hx);
else cover(p,tree[p].cov+x,tree[p].cov+hx);
}
void pushdown(int p)
{
change(p<<1,tree[p].add,tree[p].hadd);
change(p<<1|1,tree[p].add,tree[p].hadd);
tree[p].add=tree[p].hadd=0;
if(tree[p].cov!=inf)
{
cover(p<<1,tree[p].cov,tree[p].hcov);
cover(p<<1|1,tree[p].cov,tree[p].hcov);
tree[p].cov=inf,tree[p].hcov=-inf;
}
}
二维线段树
P3437 [POI2006]TET-Tetris 3D,即在一定面积上操作,其余和一位一致。
在原来的线段树上开 tag 和其他标记,每次同时更新 tag 和其他。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号