【做题记录】[NOIP2016 普及组] 魔法阵
2016年普及组T4
题意:
给定一系列元素 \(\{X_i\}\) ,求满足以下不等式的每一个元素作为 \(a,b,c,d\) 的出现次数 。
\[\begin{cases}X_a<X_b<X_c<X_d \\ X_a-X_b=2\times (X_d-X_c) \\X_b-X_a<\dfrac{X_c-X_b}{3}\end{cases}
\]
题解:
设 \(X_d-X_c=t\) ,则 \(X_a-X_b=2\times t\) 。
带入第三个式子,可得:\(2\times t<\dfrac{X_c-X_b}{3}\) 。
变形得:\(6\times t+k=X_c-X_b\) ,其中 \(1\le k\le n\) 。
因为 \(A\ge 1\) 且 \(D\le n\) ,所以 \(1\le9\times t \le n-1\) 。
则有了这么一幅图:
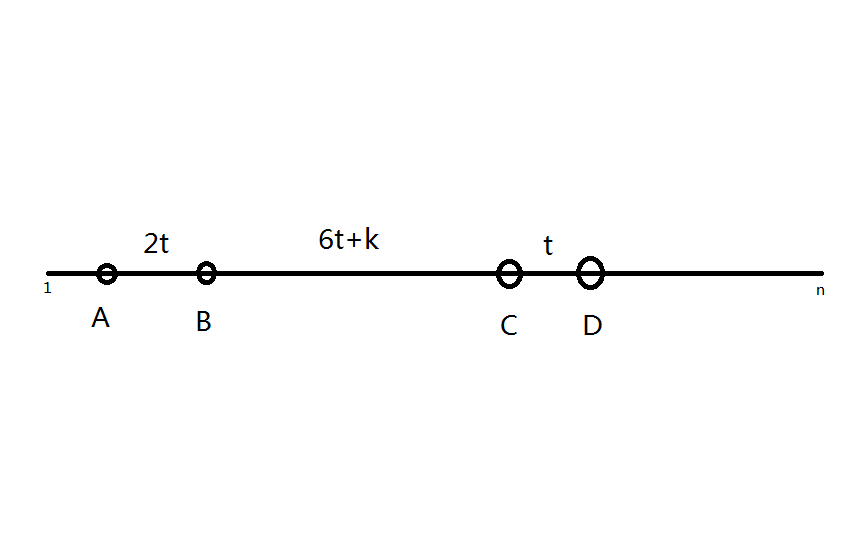
考虑枚举 \(t\) :
-
枚举 \(A=[n-9\times t-1,\dots,1]\) :
对于一对 \([A,B]\) ,\([C,D]\) 的最小值当 \(k=1\) 时取到 。而对于一对能形成魔法阵的 \([X_c,X_d]\) ,\([X_i(X_i>=X_c),X_j(X_j>X_d)]\) ,也能形成魔法阵 。则可以用后缀和优化 。
-
枚举 \(D=[2+9\times t,\dots,n]\) :同理,用前缀和优化 。
代码:
int n,m,a[Maxn],cnt[Maxn],ans[4][Maxn];
n=rd(),m=rd();
for(int i=1;i<=m;i++) a[i]=rd(),cnt[a[i]]++;
for(int t=1,tmp;9*t<n;t++)
{
tmp=0; for(int A=n-t*9-1;A>=1;A--)
{
int D=A+t*9+1,B=A+2*t,C=D-t;
tmp+=cnt[C]*cnt[D];
ans[0][A]+=tmp*cnt[B];
ans[1][B]+=tmp*cnt[A];
}
tmp=0; for(int D=t*9+2;D<=n;D++)
{
int A=D-t*9-1,B=A+t*2,C=D-t;
tmp+=cnt[A]*cnt[B];
ans[2][C]+=tmp*cnt[D];
ans[3][D]+=tmp*cnt[C];
}
}
for(int i=1;i<=m;i++) printf("%d %d %d %d\n",ans[0][a[i]],ans[1][a[i]],ans[2][a[i]],ans[3][a[i]]);


 浙公网安备 33010602011771号
浙公网安备 33010602011771号