2-SAT
非常好的博客:panyf 的 2-sat 学习笔记。
定义及实现
2-sat,简单的说就是给出 \(n\) 个集合,每个集合有两个元素,已知若干个 \(<a,b>\) ,表示 \(a\) 与 \(b\) 矛盾(其中 \(a\) 与 \(b\) 属于不同的集合)。然后从每个集合选择一个元素,判断能否一共选 \(n\) 个两两不矛盾的元素。显然可能有多种选择方案,一般题中只需要求出一种即可 。
因此,可以用强联通分量解决 2-sat 问题。
存图
对于每个变量 \(x\),我们建立两个点:\(x, \neg x\) 分别表示变量 \(x\) 取 true 和取 false。所以, 图的节点个数是两倍的变量个数 。在存储方式上,可以给第 \(i\) 个变量标号为 \(i\),其对应的反值标号为 \(i + n\)。
建图
边 \(u \rightarrow v\) 表示 「若 \(u\) 则 \(v\)」,其逆否命题为 \(\neg v \rightarrow \neg u\),表示「若非 \(v\) 则非 \(u\)」。对于每条二元限制,将其对应的命题与逆否命题的边连上,缺一不可。
- 对于 $a_i = \operatorname{true} $ 连边 $ \neg a_i \rightarrow a_i $ 「可以理解为:表示如果 \(i\) 选了
false那么 \(i\) 必须要是true与 \(i\) 只能选一个true或者false矛盾,强迫 \(i\) 只能是true」。 - 对于 $a_i = \operatorname{false} $ 连边 $ a_i \rightarrow \neg a_i $
- 对于 $ a \operatorname{or} b = \operatorname{true}$,连边 $\neg a\rightarrow b $ 和 $ \neg b\rightarrow a$ 「可以理解为:若 \(a\) 假则 \(b\) 必真,若 \(b\) 假则 \(a\) 必真」。
- 对于 $ a \operatorname{or} b = \operatorname{false}$,连边 $a\rightarrow \neg a $ 和 $ b\rightarrow \neg b$
- 对于 $ a \operatorname{and} b = \operatorname{false}$,连边 $a\rightarrow \neg b $ 和 $ b\rightarrow \neg a$
- 对于 $ a \operatorname{and} b = \operatorname{true}$,连边 $ \neg a\rightarrow a $ 和 $ \neg b\rightarrow b$
- 对于 $ a \ne b $,连边 $a \rightarrow \neg b $ 、 $ \neg a \rightarrow b $ 、 $b \rightarrow \neg a $ 、 $ \neg b \rightarrow a $
- 对于 $ a = b $,连边 $ a \rightarrow b $ 、 $ \neg a \rightarrow \neg b $ 、 $b \rightarrow a $ 、 $ \neg b \rightarrow \neg a $
可以看到,同一强连通分量内的变量值一定是相等的。也就是说,如果 \(x\) 与 \(\neg x\) 在同一强连通分量内部,一定无解。反之,就一定有解了。
但是,对于一组布尔方程,可能会有多组解同时成立。判断给每个布尔变量赋的值,只需要 当 \(x\) 所在的强连通分量的拓扑序在 \(\neg x\) 所在的强连通分量的拓扑序之后取 \(x\) 为真就可以了。
Tarjan 求解 2-sat
Tarjan 可以在 \(\mathcal{O(n)}\) 的时间范围内求出 2-sat 的一组解。
如果 \(i\) 与 \(\neg i\) 属于同一个强联通分量中,那么无解(一个强联通分量重的点只能同时选或同时不选)。
构造方案:
Tarjan 对强联通分量的拓扑排序时逆序的,序号小的不可能到达序号大的。如果 \(bel_i<bel_{i+n}\),则 \(i\) 所在的强联通分量不会推出 \(i+n\),因此不产生矛盾,选择 \(i\);反之,则选择 \(i+n\)。
所以求出的一组解为 \(bel_i<bel_{i+n}\)。
DFS 求解 2-sat
有些题目要求某些条件优先满足,比如第 \(i\) 位优先选择 \(0/1\) 之类,可以采用 DFS 的方式求解。
相当于二分图染色,如果染过了就不染,如果自己的反面染过了就返回失败。
这样最坏复杂度是 \(\mathcal{O(nm)}\) 的,但是能够解决优先的问题。
常见技巧 - 前缀优化建图
假设有这么一个限制:在 \(n(n\le 10^5)\) 个条件中只能有一个是 true,其他都是 false。
那么如果按照上面的方法需要连接 \(n^2\) 条边,显然会爆炸,多以考虑用前缀的方式连接。
我们在原来的基础上新建 \(4n\) 个点:
- \(T-right_i\) 用来传递 \([1,i]\) 之间的点是否有
true; - \(F-right_i\) 用来传递 \([1,i]\) 之间是否已经有点被强制选择
false,若有则后面的点也被强制选择; - \(T-left_i\) 几乎同上,传递 \([i,n]\) 之间是否有
true; - \(F-left_i\) 用于传递向左的强制信息。
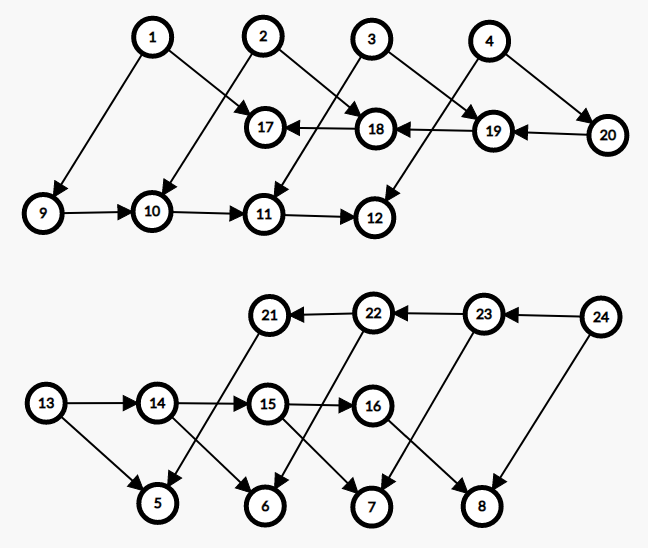
总而言之两排向右的点传递从左到右的强制信息,两排向左的点传递从右到左的强制信息。
最终的点数 \(6n\),边数 \(10n\)(其中传递信息共 \(8n\),限制信息 \(2n\))。
需要注意的问题
\(n\) 个点中恰好只有一个点为 true 怎么办?这是 \(K-sat\)!!需要将条件转化为权值 \(\le x\) 的点中是否已经选择了。
例题
三个模板题:P4782 【模板】2-SAT 问题,P4171 [JSOI2010]满汉全席(Tarjan 求解),P6378 [PA2010] Riddle(前缀优化建图),CF568C New Language(DFS 求解)
P3825 [NOI2017] 游戏
假设没有 \(x\) 赛道,那么只剩下了 \(a,b,c\),每一次只有两种选择。
我们可以设 \(aB,bA,cA\) 表示选择 \(A\) 集合,设 \(aC,bC,cB\) 表示 \(B\) 集合,直接跑 2-sat 即可,解决了没有 \(x\) 的情况(记得有一大堆的特判需要注意)。
之后我们发现 \(d\) 非常小,考虑暴力枚举 \(x\) 的选择情况?
\(3^8=6561\),加上 \(2n\le 10^5\),若直接暴力枚举复杂度是 \(6.561\times 10^8\) 的,且时限 \(1s\),看起来不太行(实践操作 \(90pts\))。
\(\bigstar\texttt{Hint}\):只用枚举每个 \(x\) 是 \(a\) 或 \(b\) 的情况,通过这样的两种情况中,\(A,B,C\) 都可以在 \(x\) 上取到。
发现这样枚举可以变为一个全局 2-sat 问题,将 \(3^8\) 变为了 \(2^8\)。
CF1215F Radio Stations
前面两个条件直接建边即可。
之后可以将所有相交的区间相连,那么答案必须是一个强联通分量。
可以将所有不相交的区间只能够选一个,那么最终的答案一定都是互不相交的。
考虑怎样将不相交的区间相连,首先肯定不能 \(n^2\) 直接判断。
那么按照上面的前缀优化暴力建边即可,有两点特别注意:
true中向右的点以右端点为关键字递增;true中向左的点以左端点为关键字递增;false中向右的点以左端点为关键字递增;false中向左的点以右端点为关键字递增。
首先需要遵循可递推性!!(因为这个调了很久很久!!!)
P5332 [JSOI2019]精准预测
给定 \(n\) 个人和 \(m\) 组限制,分为两种:
- 如果 \(x\) 在 \(t\) 时间前死了,则 \(y\) 在 \(t+1\) 时间前也死了。
- 如果 \(x\) 在 \(t\) 时间还活着,则 \(y\) 在 \(t\) 时间前死了。
请你对每一个人计算出在 \(T+1\) 时间时可能与其同时存活的人数。如果这个人在 \(T+1\) 时刻必然死则答案为 \(0\)。
\(n\leq 5\times 10^4,m\leq 10^5,T\leq 10^6\)。
先考虑一个的暴力:对于每一个人建立 \(2T\) 个节点,表示在某一时刻它是活着的还是死的。
如果一个人在 \(t\) 时刻死亡,一定在 \(t+1\) 时刻死亡;如果一个人在 \(t\) 时间活着,一定在 \(t-1\) 时间活着。之后好像根据信息连边就可以判断出了一组解。因为对于所有限制只有 \(m\) 个节点是有用的,所以可以只保留关键点,剩余 \(n+2m\) 个点。
之后就不会了,想到了一个可能是假算的暴力:对于每个 \((i,T+1,\text{Live})\) 判断能够到达的其他人的死亡点,加上必然死亡的人就是不能和它一起存活的人,这样是 \(\mathcal{O(n(n+m))}\) 的。
有发现整一张图是一个 DAG,只会有 \(\text{Live}\) 向 \(\text{Dead}\) 方向的边,但是需要判断每个点到达其他店的情况,不会了。
\(\bigstar\texttt{Hint-1}\):发现假算其实是正解!在 DAG 上求解每个点能够到达的终点个数可以用 bitset 直接优化掉!在 DAG 上每一位记下能够到达的 \((i,T+1,\text{Dead})\) 点的个数,计算答案即可。
但是,发现空间还是开不下怎么办?
\(\bigstar\texttt{Hint-2}\):分为多次求解,找一个块长 \(S\),第一次求出到 \(\text{Dead}([1,S],T+1)\) 的所有点的可达性,第二次求出到 \(\text{Dead}([S+1,2S],T+1)\) 的所有点的可达性,以此类推。设 \(S=10^4\) 比较合适。
但是,还是会被卡常怎么办?
\(\bigstar\texttt{Hint-3}\):将每次的 \(t+1\) 改为比 \(t\) 大的第一个虚拟节点,这样减少了 \(2m\) 个节点。
CF1007D Ants
给定一棵 \(n\) 个点树,树上有 \(m\) 只蚂蚁。每个蚂蚁有一个代表颜色 \(i\) 和两个需求 \((a_i,b_i),(c_i,d_i)\) 表示在树上 \(a_i\) 到 \(b_i\) 的路径或者 \(c_i\) 到 \(d_i\) 的路径上至少有一条的颜色全部为 \(col_i\)。
如果存在一种数的染色方案,请输出,否则输出不可行。
\(n\le 10^5,m\le 10^4\)。
发现限制有许多中颜色,需要考虑将限制分为两类。考虑 \(T_{i,1},F_{i,1},T_{i,2},F_{i,2}\) 分别表示第 \(i\) 只蚂蚁第 \(p\) 个要求是否实现。当然有他们其中至少有一个需要实现。
那么树剖一下,线段树优化一下,标记在某一条边上的节点有哪些,显然有不同颜色中间只能够满足一个。
似乎这样可能会出现 \(m^2\) 级别的边,经过 \(\texttt{Z}\color{red}{\texttt{CETHAN}}\) 指点迷津,发现在上面树剖剖出来的线段树节点上其实不用颜色两两连接,可以前缀优化建图!
咕咕咕


