生成树相关
最小、次小生成树
如何生成最小、次小生成树?
Kruskal
就是暴力地将所有边排序,从小到大查看是否可以将两个连通块联通,复杂度为 \(\mathcal{O((n+m)\log n)}\)(如果用斐波那契对可以降到 \(\mathcal{O(n\log n+m)}\))。
Prim?咕咕咕
Boruvka?咕咕咕
非严格次小生成树
枚举每一条边,倍增求生成树中 \(u\) 到 \(v\) 的路径中非严格小于这条边的最大权值,计算如果替换后的生成树大小。
严格最小生成树
同样倍增,求路径中严格小于新增边权的最大边,其余同上。\(\texttt{code}\)
DAG 上的最小生成树
给定一张 DAG,保证从 \(1\) 开始能够到达所有点,要求生成一棵从 \(1\) 开始的外向树遍及所有点,并且路径长度之和最小。
\(n\le 10^5,m\le 10^6\)。
先用一遍 \(\text{dfs}\) 求出可以到达的点的个数以及可能经过的所有边。
- 按照拓扑序从小到大给每个点赋上权值;
- 将本来的以边权从小到大排序改为:先以终点的拓扑序从小到大,若拓扑序相同再以边权排序。
为什么呢?这样可以保证我们每次连上的边都是合法的、与 \(1\) 直接或间接相连的。
瓶颈生成树?咕咕咕
最小瓶颈路?咕咕咕
Kruskal 重构树
定义
可悲的 Kruskal 只能满足两点之间路径最大边权最小,
贪婪的人们从不满足于弱小的 Kruskal,可悲的天才们沉迷于更为强大的结构,并残忍侵占了弱小的空间复杂度,将恶毒的眼光投向了可悲的时间复杂度。
于是我们考虑这样一件事情,那就是,用 Kruskal 够构建出一棵更为厉害的树,考虑将它叫做 Kruskal 重构树。
重构树将边权转移到点上,并每次连接两个连通块时都将两个连通块的顶部连到新建的点上。
比如我们现在有这样一棵树:
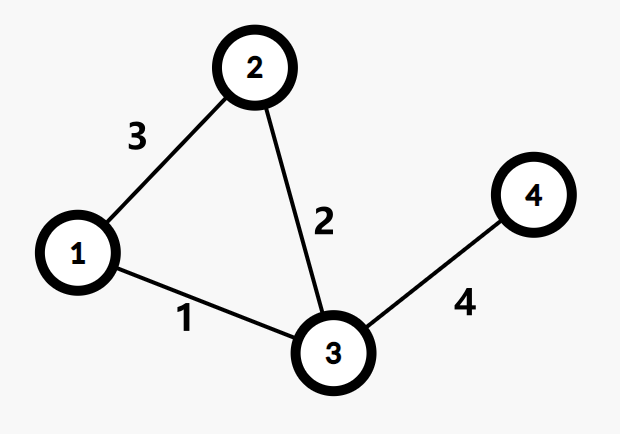
就可以生成这样一棵树:
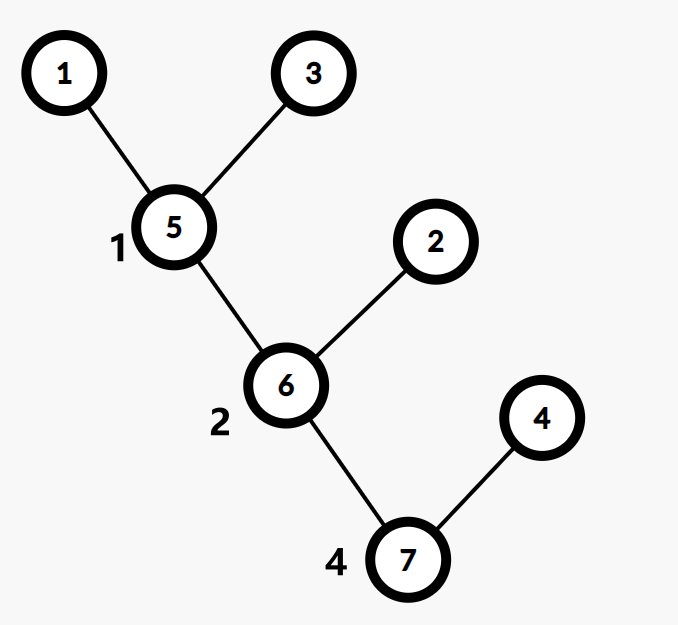
性质
-
它是一棵二叉树,满足堆的性质。
-
两个点的 \(lca\) 为这两个点的路径上的边权最小 \(/\) 大值。
-
一个根节点以下的所有点都可以用边权不超过 \(/\) 少于根节点权值的边联通,也就是说,到点 \(x\) 的简单路径上最小边权最大值 \(\le val\) 的所有点 \(y\) 均在 Kruskal 重构树上的某一棵子树内,且恰好为该子树的所有叶子节点。
那么,根据这个性质,我们就可以快速解决 P4768 [NOI2018] 归程 啦!
最小直径生成树
给定一张简单无向图,要求求出这张图的最小直径生成树。
\(n\le 200,n-1\le m\le \frac{n(n-1)}{2}\)。
图的绝对重心
如果需要求解树的最小直径生成树,我们需要先找到图的绝对重心。
绝对重心可以在一条边上或一个点上,这个中心到所有点的最短路的最大值最小。
图的绝对重心在点上
那么直接求出每一个点到达的最远的点,用到达最远的点的距离的两倍更新答案。
图的绝对重心在边上
考虑如果重心在边 \(u-v\) 上对于图中一点 \(i\),图的绝对重心到它的距离为 \(\min\{d_{u,i}+x,d_{v,i}+(w-x)\}\)。
其中 \(d\) 是两点之间距离,\(w\) 是这条边的边长,\(x\) 是这个点在这条边上到 \(u\) 的距离。
随着 \(x\) 不断增大,\(i\) 到重心的距离会先增大后减小,可以看 oi-wiki 上的图:
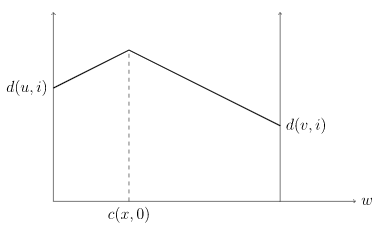
那么如果将所有 \(n\) 个点的折线都画出来,重心到所有点距离的最大值的函数如下所示:
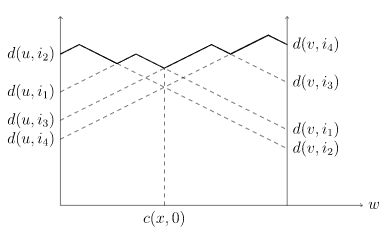
那么最低点的横坐标就是重心距离 \(u\) 的距离,纵坐标就是直径的一半长。
那么我们只用预处理出对于每个点距离它距离 \(1-n\) 近的点的编号,利用上面折线相交的特点记录最小值即可。
寻找重心部分代码如下:
for(int i=1;i<=n;i++) ans=min(ans,ds[i][rk[i][n]]*2);
for(int i=1,u,v,w;i<=m;i++)
{
u=e[i].u,v=e[i].v,w=e[i].w;
for(int Last=n,Now=n-1;Now>=1;Now--)
if(ds[v][rk[u][Now]]>ds[v][rk[u][Last]])
ans=min(ans,ds[u][rk[u][Now]]+ds[v][rk[u][Last]]+w),Last=Now;
}
最小直径生成树
用上面两种方式更新答案,可以得到图的绝对重心。
从图的绝对重心开始,生成一棵最短路树,就可以得到最小直径生成树。
模板题:CF266D BerDonalds,CF gym102391 I,SP735 MDST - Minimum Diameter Spanning Tree,SP1479 PT07C - The GbAaY Kingdom(但是两道 SPOJ 的题一直不知道为什么 WA!)。


