计算几何初步
两点之间距离
欧氏距离
即欧几里得距离。
平面内两点的距离为
立体空间内两点的距离为
\(\dots\)
\(n\) 维空间内两点的距离为
曼哈顿距离
二维空间内,两点之间距离为
\(n\) 维空间内两点的距离为
性质 \(-\) 三角形不等式:从点 \(i\) 到 \(i\) 的直接距离不会大于途经的任何其它点 \(k\) 的距离。
切比雪夫距离
二维空间内,两点之间距离为
曼哈顿距离与切比雪夫距离的相互转化
设 \(A(x_1,y_1),B(x_2,y_2)\) ,
-
曼哈顿坐标系是通过切比雪夫坐标系旋转 \(45^\circ\) 后,再缩小到原来的一半得到的
-
把每个点 \((x,y)\) 转化为 \((x+y,x-y)\) ,新坐标系下的切比雪夫距离 就是 原坐标系下的曼哈顿距离 。
-
把每个点 \((x,y)\) 转化为 \((\dfrac{x+y}{2},\dfrac{x-y}{2})\) ,新坐标系下的曼哈顿距离 就是 原坐标系下的切比雪夫距离 。
例题
P5098 [USACO04OPEN]Cave Cows 3
对于式子 \(|x_1-x_2|+|y_1-y_2|\) ,可以假设 \(x_1-x_2\ge 0\) ,根据 \(y_1-y_2\) 正负分类讨论:
- \(y_1-y_2\ge 0\) :
- \(y_1-y_2< 0\) :
分别求出 \(x+y\) 和 \(x-y\) 的最大、最小值之差即可。
P4648 [IOI2007] pairs 动物对数 (曼哈顿距离转切比雪夫距离)
P3964 [TJOI2013]松鼠聚会 (切比雪夫距离转曼哈顿距离)
向量基本运算
\(\overrightarrow{AB}=\dfrac{y_B-y_A}{x_B-x_A}\)
向量点积:
\(\overrightarrow{AB}\cdot\overrightarrow{CD}=x_1x_2+y_1y_2=|AB||CD|\cos a\)
向量叉积的判断与应用

如图所示:
-
如果 \(\overrightarrow{A}\cdot\overrightarrow{B}>0\),则方向基本相同,夹角在 \(0^o\) 到 \(90^o\) 之间。
-
如果 \(\overrightarrow{A}\cdot\overrightarrow{B}=0\),正交,方向垂直。
-
如果 \(\overrightarrow{A}\cdot\overrightarrow{B}<0\),则方向基本相反,夹角在 \(90^o\) 到 \(180^o\) 之间。
向量叉积:
\(\overrightarrow{AB}\times\overrightarrow{CD}=x_1y_2-x_1y_2=|AB||CD|\sin a\)
向量叉积的判断与应用

右手定则:将手放在 \(\overrightarrow{AB}\) 方向上,手指弯曲方向为叉积正。
-
如果 \(\overrightarrow{AB}\times\overrightarrow{CD}>0\),则 \(\overrightarrow{CD}\) 在 \(\overrightarrow{AB}\) 的逆时针 \(180^o\) 以内。
-
如果 \(\overrightarrow{AB}\times\overrightarrow{CD}=0\),则两个向量在同一条直线上。
-
如果 \(\overrightarrow{AB}\times\overrightarrow{CD}<0\),则 \(\overrightarrow{CD}\) 在 \(\overrightarrow{AB}\) 的顺时针 \(180^o\) 以内。
我们就可以利用叉积来维护凸包以及多边形面积。
向量旋转:
让点 \((x1,y1)\) 绕点 \((x2,y2)\) 旋转 \(t^o\):(记 \(x1-x2=X,y1-y2=Y\))
\(x=X\times\cos t-Y\times\sin t+x2\)
\(y=X\times\sin t+Y\times\cos t+y2\)
用矩阵的方式表示为:
极角排序
选择一个点,用向量叉积排序。
判断
判断点是否在线段上
设点为 \(P\),线段为 \(AB\)。
则判断依据为:\(\overrightarrow{PA}\times\overrightarrow{PA}=0\)
判断两个线段是否相交
设线段为 \(P1P2\) 和 \(Q1Q2\)。
-
先快速排除不可能的情况:\(P1P2\) 与 \(Q1Q2\) 构成的矩形一定相交。
-
跨立测验:若 \(P1P2\) 跨立 \(Q1Q2\),则 线段 \(P1Q1\) 和 \(P2Q1\) 位于线段 \(Q2Q1\) 的两侧。线段 \(P1Q1\) 和 \(P2Q1\) 分别于 \(Q2Q1\) 的叉积数值乘起来小于 \(0\) 即可。
判断线段与直线是否相交
直接用上面跨立测验即可。
判断点是否在多边形之内
过点 \((x,y)\) 向左做平行于 \(x\) 轴的射线,计算与多边形交点数量即可。
即判断 \((-\infty,y)-(x,y)\) 与 多边形的交点个数。
特殊情况:
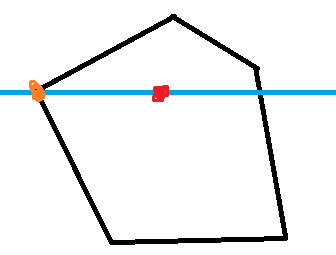
这时只能计算一次。
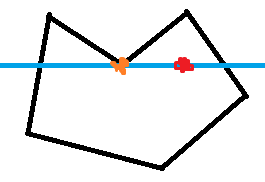
这时需计算两次。
若出现与边界重合时,忽略线段。
判断线段是否在多边形内部
用上面的方法,计算与多边形交点个数。
计算
计算点到线段/直线/多边形的最近点
直接解方程即可
计算旋转卡壳/凸包直径
固定一条边,用另一条平行的边找到与多边形相交的最远位置(找最远位置可以用三角形面积和双指针)
半平面与半平面交
半平面:如 \(ax+by+c\ge 0\) 的方程的解集(点集),如下图所示。
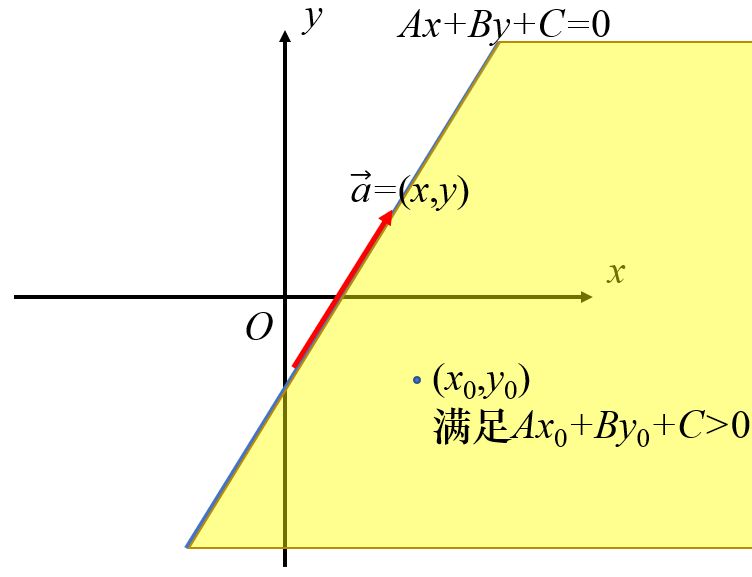
半平面交:许多半平面的解集的交。
按照极角排序,维护一个单调队列。
P4196 [CQOI2006]凸多边形 /【模板】半平面交
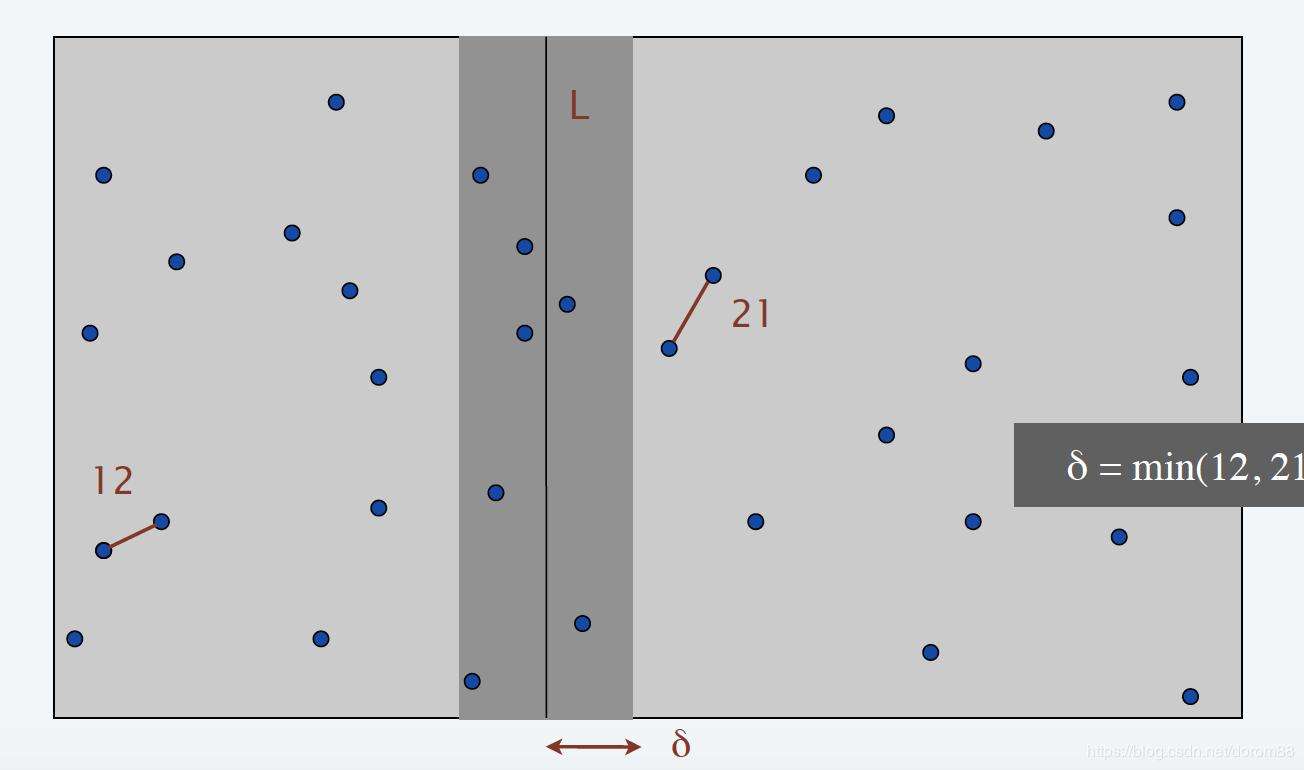
平面最近点对
分治解决,合并的时候只有距离分解线不超过两边答案的最小值的点才可能成为答案。