常见排序算法

常见排序算法

排序算法比较

排序算法	最坏	最优	平均	空间	稳定性	内部 \(\texttt{or}\) 外部排序
冒泡排序	\(O(n^2)\)	\(O(n)\)	\(O(n^2)\)	\(O(1)\)	是	In
直接插入排序	\(O(n^2)\)	\(O(n)\)	\(O(n^2)\)	\(O(1)\)	是	In
选择排序	\(O(n^2)\)	\(O(n^2)\)	\(O(n^2)\)	\(O(1)\)	\(/\)	In
归并排序	\(O(n\log n)\)	\(O(n\log n)\)	\(O(n\log n)\)	\(O(n)\)	是	Out
快速排序	\(O(n^2)\)	\(O(n\log n)\)	\(O(n\log n)\)	\(O(n\log n)\)	\(/\)	In
希尔排序	\(O(n^2)\)	\(O(n\log_2 n)\)	\(O(n^{1.3})\)	\(O(1)\)	\(/\)	In
堆排序	\(O(n\log n)\)	\(O(n\log n)\)	\(O(n\log n)\)	\(O(1)\)	\(/\)	In
桶排序	\(O(n^2)\)	\(O(n + k)\)	\(O(n+k)\)	\(O(n+k)\)	是	Out
计数排序	\(O(n + k)\)	\(O(n + k)\)	\(O(n + k)\)	\(O(k)\)	是	Out
基数排序	\(O(n\times k)\)	\(O(n\times k)\)	\(O(n\times k)\)	\(O(n+k)\)	是	Out

各种排序算法注意点与实现：

冒泡排序

当数据已经正序时，最优；反序时最坏。

插入排序

直接插入排序

折半插入排序

将向前找的操作改为二分

直接选择排序

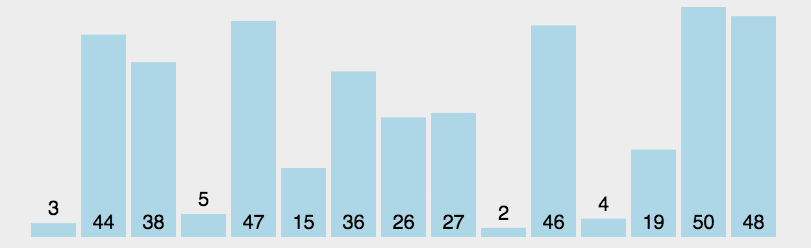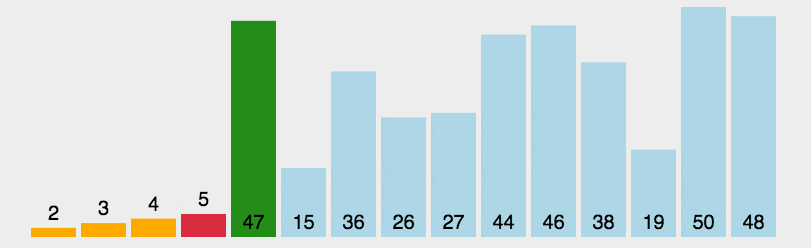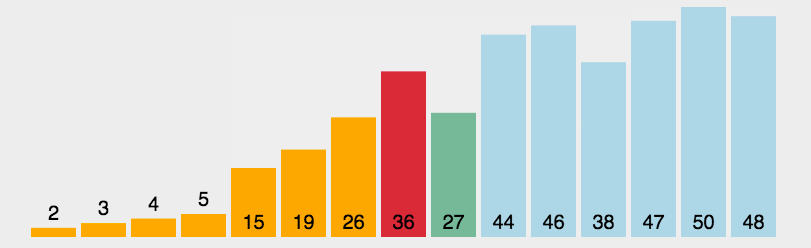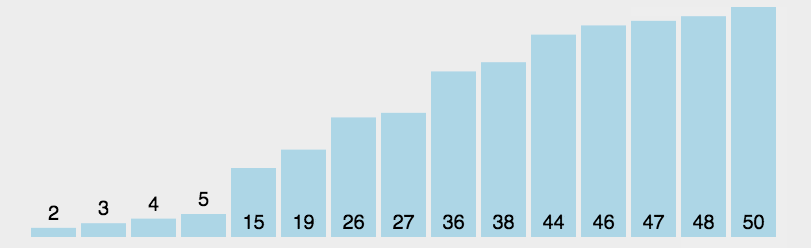
归并排序

这是因为归并排序的合并函数，在合并两个有序数组为一个有序数组时，需要借助额外的存储空间。临时内存空间最大不会超过 \(n\) 个数据的大小，所以空间复杂度是 \(O(n)\) 。

快速排序

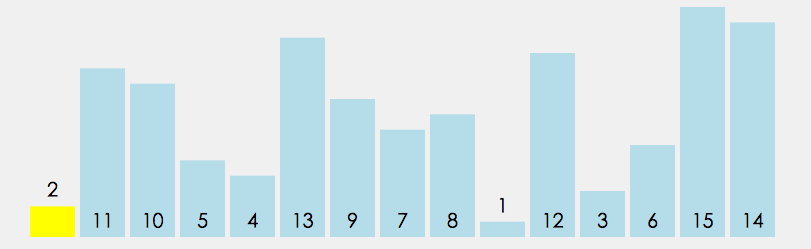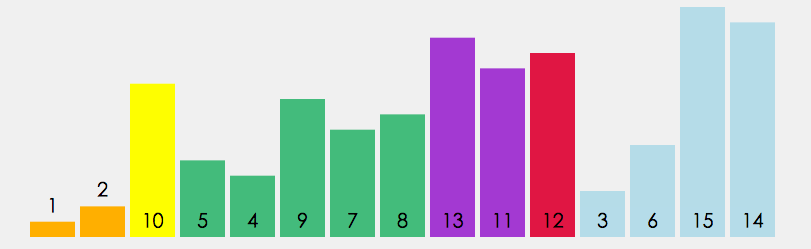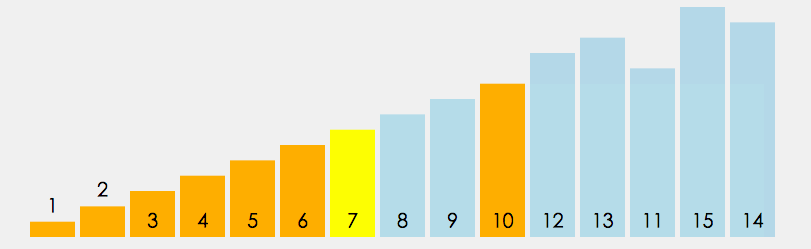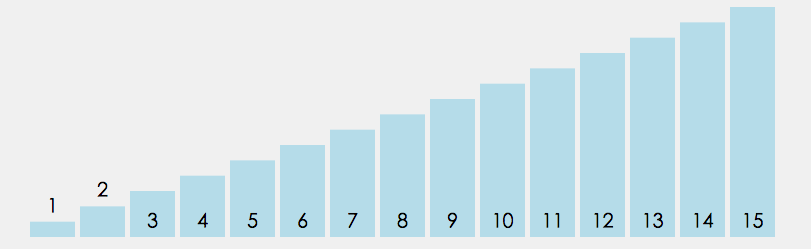
方法一：

const quickSort1 = arr => {
	if (arr.length <= 1) {
		return arr;
	}
	//取基准点
	const midIndex = Math.floor(arr.length / 2);
	//取基准点的值，splice(index,1) 则返回的是含有被删除的元素的数组。
	const valArr = arr.splice(midIndex, 1);
	const midIndexVal = valArr[0];
	const left = []; //存放比基准点小的数组
	const right = []; //存放比基准点大的数组
	//遍历数组，进行判断分配
	for (let i = 0; i < arr.length; i++) {
		if (arr[i] < midIndexVal) {
			left.push(arr[i]); //比基准点小的放在左边数组
		} else {
			right.push(arr[i]); //比基准点大的放在右边数组
		}
	}
	//递归执行以上操作，对左右两个数组进行操作，直到数组长度为 <= 1
	return quickSort1(left).concat(midIndexVal, quickSort1(right));
};
const array2 = [5, 4, 3, 2, 1];
console.log('quickSort1 ', quickSort1(array2));
// quickSort1: [1, 2, 3, 4, 5]

方法二：

// 快速排序
const quickSort = (arr, left, right) => {
	let len = arr.length,
		partitionIndex;
	left = typeof left != 'number' ? 0 : left;
	right = typeof right != 'number' ? len - 1 : right;

	if (left < right) {
		partitionIndex = partition(arr, left, right);
		quickSort(arr, left, partitionIndex - 1);
		quickSort(arr, partitionIndex + 1, right);
	}
	return arr;
};

const partition = (arr, left, right) => {
	//分区操作
	let pivot = left, //设定基准值（pivot）
		index = pivot + 1;
	for (let i = index; i <= right; i++) {
		if (arr[i] < arr[pivot]) {
			swap(arr, i, index);
			index++;
		}
	}
	swap(arr, pivot, index - 1);
	return index - 1;
};

const swap = (arr, i, j) => {
	let temp = arr[i];
	arr[i] = arr[j];
	arr[j] = temp;
};

希尔排序

1. 先将整个待排序的记录序列分割成为若干子序列。

2. 分别进行直接插入排序。

3. 待整个序列中的记录基本有序时，再对全体记录进行依次直接插入排序。

堆排序

储存

堆是通过以为数组实现的，分为大根堆和小根堆。

• 父节点 \(i\) 的左子节点在位置 \((2\times i+1)\)

• 父节点 \(i\) 的右子节点在位置 \((2\times i+2)\)

• 子节点 \(i\) 的父节点在位置 \(\left\lfloor\dfrac{i-1}{2}\right\rfloor\)

复杂度

• 时间复杂度：最好 \(O(\log n)\) ，最坏 \(O(\log n)\) ，平均 \(O(\log n)\) 。

  • 建堆： \(O(n)\) 。

  • 堆调整： \(O(\log n)\) 。

计数排序

相当于 \(\text{STL}\) 中的 map<> mp 。

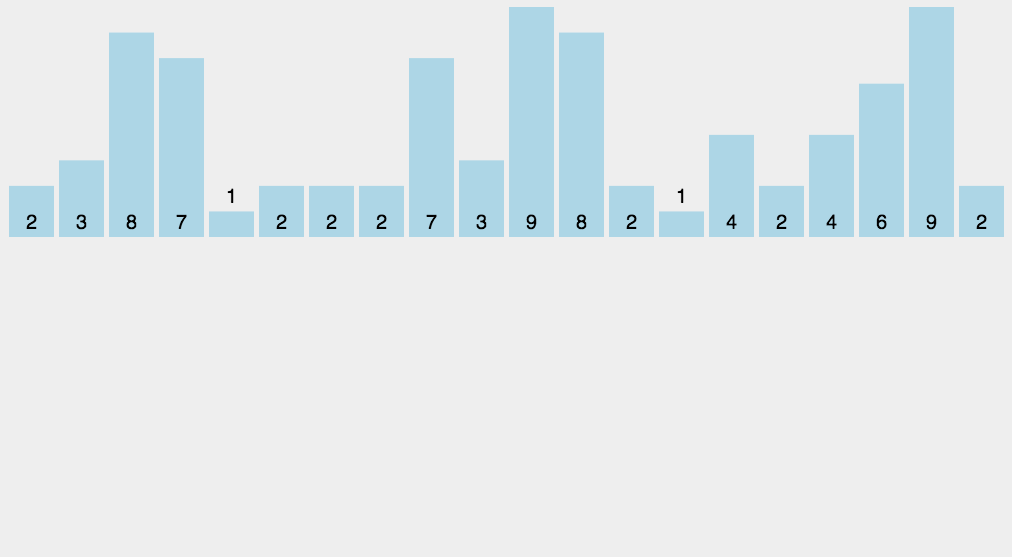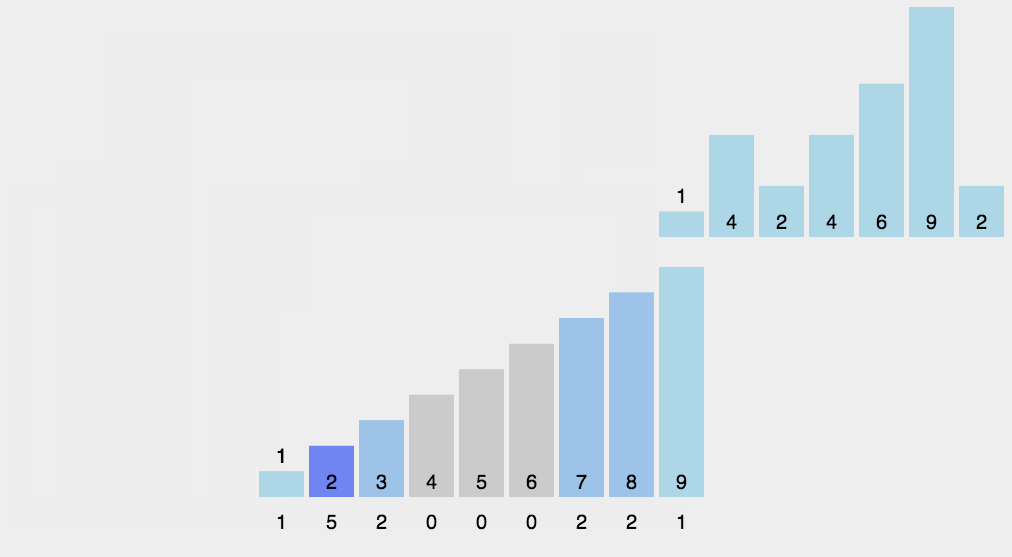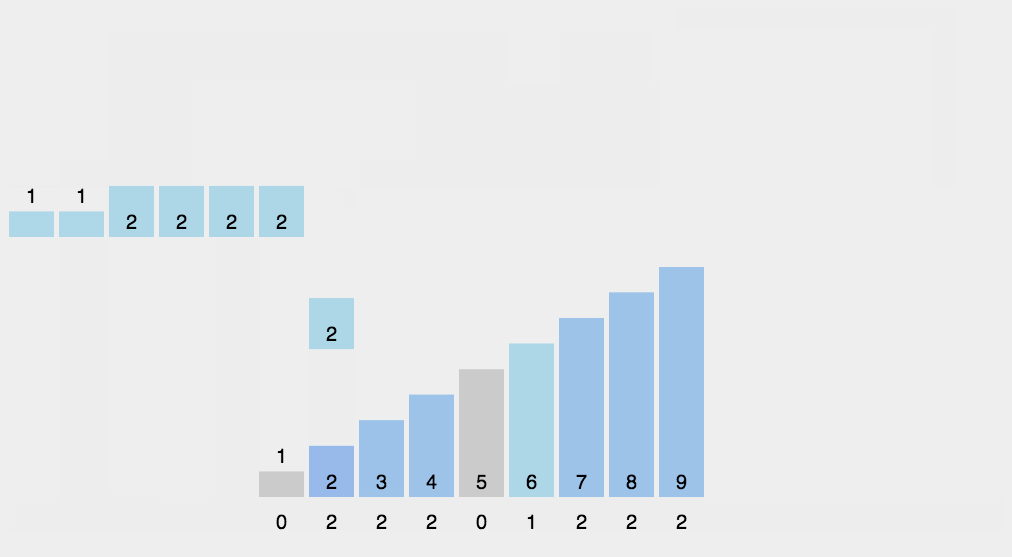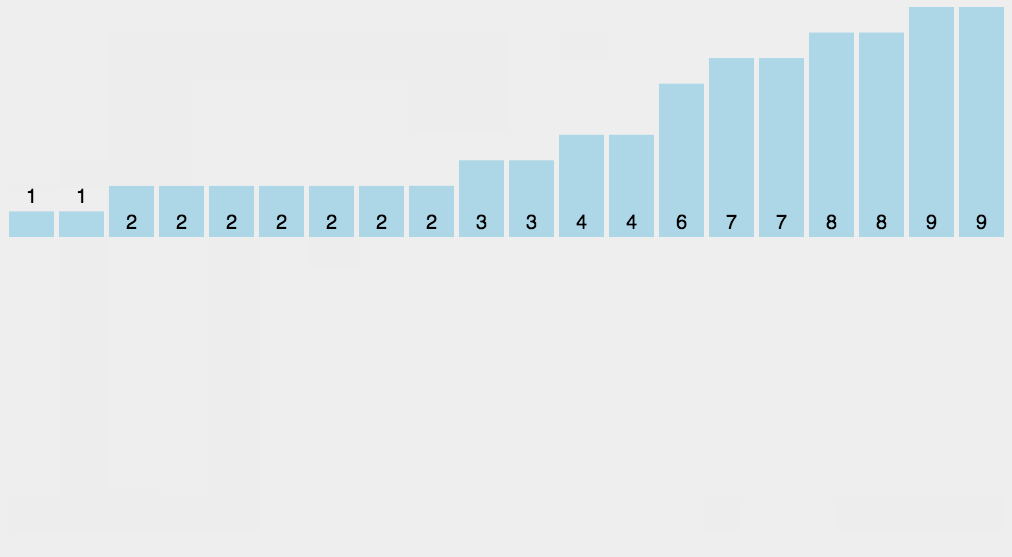
基数排序

错题

快速排序找第 \(k\) 大数

应用快速排序的分治思想，可以实现一个求第 \(k\) 大数的程序。假定不考虑极端的最坏情况，理论上可以实现的最低的算法时间复杂度为:

错误：\(O(n\log n)\)

正确：\(O(n)\)

事实上，在做的时候，分治的另一个区间是可以抛掉的。

也就是说，虽然进行了二分，\(T(n)=n+\frac{n}{2}+\frac{n}{4}+\dots\) ，因此渐进复杂度为O（n）。