图的匹配—网络流

第一部分：图的匹配—二分图

这是第二部分：网络流

网络流 \(24\) 题题解

网络流基础建模

费用流基础建模

（\(\uparrow\) 学习资料）

最大流求解

P3376 【模板】网络最大流

P4722 【模板】最大流 加强版 / 预流推进

EK 算法

复杂度：\(O(nm^2)\)，所以，关于 EK，他死了。

$\texttt{code}$

struct EK
{
	 #define Maxn 点数
	 #define Maxm 边数 
	 int _n,tot=1;
	 int pre[Maxn],hea[Maxn],ver[Maxm<<1],nex[Maxm<<1];
	 ll sum,ds[Maxn],edg[Maxm<<1];
	 bool vis[Maxn];
	 inline void init(int n)
	 {
	 	 //tot=1;
	 	 _n=n;
	 }
	 bool dfs(int s,int t)
	 {
		 memset(vis,false,sizeof(vis));
		 queue<int> q; q.push(s),vis[s]=1,ds[s]=inf;
		 while(!q.empty())
		 {
		 	 int cur=q.front(); q.pop();
		 	 for(int i=hea[cur];i;i=nex[i]) if(edg[i] && !vis[ver[i]])
		 	 	 {
		 	 	 	 pre[ver[i]]=i,vis[ver[i]]=true;
		 	 	 	 ds[ver[i]]=min(ds[cur],edg[i]);
		 	 	 	 if(ver[i]==t) return true;
		 	 	 	 q.push(ver[i]);
				 }
		 }
		 return false;
	 }
	 ll solve(int s,int t)
	 {
	 	 sum=0;
		 while(dfs(s,t))
		 {
		 	 for(int x=t,i;x!=s;)
		 	 	 i=pre[x],edg[i]-=ds[t],edg[i^1]+=ds[t],x=ver[i^1];
			 sum+=ds[t];
		 }
		 return sum;
	 }
	 #undef Maxn
	 #undef Maxm
}G;

dinic 算法

最坏复杂度为 \(O(n^2m)\) （一般跑不到这个上界），而在单位流量的二分图中，复杂度可以只用 \(O(\sqrt{n}m)\)。

• 多路增广：每次增广前，我们先用 BFS 来将图分层,建立残量网络。设源点的层数为 \(0\) ，那么一个点的层数便是它离源点的最近距离。

• 当前弧优化：如果一条边已经被增广过，那么它就没有可能被增广第二次。那么，我们下一次进行增广的时候，就可以不必再走那些已经被增广过的边。

  在建立残量网络的时候对 \(cur[]\) 进行初始化，表示这一轮寻找曾增广路的 \(tmphead[]\) ：

for(int i=1;i<=n;i++) cur[i]=hea[i];

之后再每一次寻找增广路的 \(dinic\) 函数中进行一下操作：

for(int i=cur[u];i && rest;i=nex[i])
{
	 cur[u]=i;
	 ... 
}

$\texttt{code}$

struct Dinic
{
	#define Maxn 点数
	#define Maxm 边数
	int tot=1;
	int hea[Maxn],nex[Maxm<<1],ver[Maxm<<1];
	int tmphea[Maxn],dep[Maxn];
	ll edg[Maxm<<1],sum;
	inline void init()
		{ tot=1,memset(hea,0,sizeof(hea)); }
	inline void add_edge(int x,int y,ll d)
	{
		ver[++tot]=y,nex[tot]=hea[x],hea[x]=tot,edg[tot]=d;
		ver[++tot]=x,nex[tot]=hea[y],hea[y]=tot,edg[tot]=0;
	}
	inline bool bfs(int s,int t)
	{
		memset(dep,0,sizeof(dep)),dep[s]=1;
		memcpy(tmphea,hea,sizeof(hea));
		queue<int> q; q.push(s);
		while(!q.empty())
		{
			int cur=q.front(); q.pop();
			if(cur==t) return true;
			for(int i=hea[cur];i;i=nex[i]) if(edg[i]>0 && !dep[ver[i]])
				dep[ver[i]]=dep[cur]+1,q.push(ver[i]);
		}
		return false;
	}
	ll dfs(int x,ll flow,int t)
	{
		if(x==t || !flow) return flow;
		ll rest=flow,tmp;
		for(int i=tmphea[x];i && rest;i=nex[i])
		{
			tmphea[x]=i;
			if(dep[ver[i]]==dep[x]+1 && edg[i]>0)
			{
				if(!(tmp = dfs(ver[i],min(edg[i],rest),t))) dep[ver[i]]=0;
				edg[i]-=tmp,edg[i^1]+=tmp,rest-=tmp;
			}
		}
		return flow-rest;
	}
	inline ll solve(int s,int t)
	{
		sum=0;
		while(bfs(s,t)) sum+=dfs(s,inf,t);
		return sum;
	}
	#undef Maxn
	#undef Maxm
}G;

ISAP

我们发现每一次都进行 \(\text{bfs}\) 太慢了，才有了 ISAP。

与 dinic 的一些区别：

• 我们将 dinic 的每一次都进行一次分层，改为进行一遍从 \(t\) 开始倒序分层，并把原来的层数加一改为层数减一。

• 我们每一次增广完一个点后都将这个点的深度提高，来保证每一条边都都会被访问过。

• 如果访问下一个点时，发现流量等于 \(0\)，在这里不再将它深度设为 \(0\)，而是继续访问。

• 如果我们发现此时 \(flow\)（到这个点时的最大流量）已经用完了，那么直接返回。

• 每次更改点的深度时都记录每一种深度上的点的个数，若某一个深度上已经没有点了，那么可以可以直接结束程序（断层了）。

该优化被称为 GAP 优化。

ISAP 也满足当前弧优化。

但是！记得需要多大的空间就开多大的空间，不然会慢很多！

最坏复杂度：\(O(n^2m)\)，同 dinic，不过常数、实际运行速度优于 dinic。

还是学学预流推进吧。。

$\texttt{code}$

struct ISAP
{
	 #define Maxn 点数
	 #define Maxm 边数 
	 int tot=1,All;
	 int dep[Maxn],cnt[Maxn];
	 int tmphea[Maxn],hea[Maxn],nex[Maxm<<1],ver[Maxm<<1];
	 ll sum,edg[Maxm<<1];
	 inline void add_edge(int x,int y,ll d)
	 {
	 	 ver[++tot]=y,nex[tot]=hea[x],hea[x]=tot,edg[tot]=d;
	 	 ver[++tot]=x,nex[tot]=hea[y],hea[y]=tot,edg[tot]=0;
	 }
	 inline void init(int n,int s,int t)
	 {
	 	 tot=1; //看情况决定是否要加 
	 	 All=n,hea[s]=hea[t]=0;
	 	 for(int i=1;i<=n;i++) hea[i]=0;
	 }
	 void bfs(int s,int t)
	 {
	 	 memset(dep,0,sizeof(dep));
	 	 memset(cnt,0,sizeof(cnt));
	 	 queue<int> q; q.push(t),dep[t]=1;
	 	 while(!q.empty())
	 	 {
	 	 	 int cur=q.front(); q.pop();
	 	 	 for(int i=hea[cur];i;i=nex[i]) if(!dep[ver[i]])
	 	 	 	 dep[ver[i]]=dep[cur]+1,q.push(ver[i]);
		 }
		 for(int i=1;i<=All;i++) cnt[dep[i]]++;
		 if(s>All) cnt[dep[s]]++,All++;
		 if(t>All) cnt[dep[t]]++,All++;
	 }
	 ll dfs(int x,ll flow,int s,int t)
	 {
	 	 if(x==t) return flow;
	 	 ll used=0,tmp;
	 	 for(int i=tmphea[x];i;i=nex[i])
	 	 {
	 	 	 tmphea[x]=i;
	 	 	 if(edg[i]>0 && dep[ver[i]]==dep[x]-1)
	 	 	 {
	 	 	 	 if((tmp = dfs(ver[i],min(flow-used,edg[i]),s,t)) > 0)
	 	 	 	 	 edg[i]-=tmp,edg[i^1]+=tmp,used+=tmp;
	 	 	 	 if(used==flow) return flow;
			 }
		 }
		 if(!(--cnt[dep[x]])) dep[s]=All+1;
		 cnt[++dep[x]]++; return used;
	 }
	 inline ll solve(int s,int t)
	 {
	 	 bfs(s,t),sum=0;
	 	 while(dep[s]<=All)
		  	 memcpy(tmphea,hea,sizeof(hea)),sum+=dfs(s,infll,s,t);
	 	 return sum;
	 }
	 #undef Maxn
	 #undef Maxm
}G;

Push-Relabel 预流推进算法—咕咕咕

HLPP 算法—复杂度：\(O(n^2\sqrt m)\)

最大流性质及应用

网络流退流

（现在的 dinic 网络流模板已经支持退流）

去掉 \(u\rightarrow v\) 的边：将 \(u\rightarrow\) 的正负流量都改为 \(0\)，从 \(u\rightarrow s,t\rightarrow v\) 跑最大流，再从 \(s\rightarrow t\) 跑最大流。

增加 \(u\rightarrow v\) 的边：直接从 \(s\rightarrow t\) 跑最大流。

P3308 [SDOI2014]LIS

（\(\uparrow\) 记得清空！！！调了一个下午）

P5295 [北京省选集训2019]图的难题

一张有 \(V\) 个点的图最多有 \(2\times V-2\) 条边（生成两棵树，任意加上一条边都会让图不成立）

则 \(E\le 2\times V-2\rightarrow E-2\times V\le -2\)。

不仅整张图需要满足这个限制，这个图的每个子图都要满足这个限制才成立。

由于如果选择了一条边，这条边的两个端点都必须选择，有依赖关系，考虑将边也转化为点。

这样，由边转化来的点的权值为 \(1\)，在原图中的点的权值为 \(-2\)，需要满足每一个选择的集合都满足上面的限制。

如果需要选择每个子图，可以考虑枚举每个点是否在这个子图中。

那么可以强制选择某一个点，计算出最大的权值（最大权闭合子图），如果最大权值大于 \(2\)，则表示不成立。

强制选点与取消可以用网络退流解决。

费用流求解

P3381 【模板】最小费用最大流

EK

也叫做 MCMF 算法。

$\texttt{code}$

#define Maxn 5005
#define Maxm 50005
#define inf 0x7f7f7f7f
int n,m,sum,hua,tot=1;
int hea[Maxn],ver[Maxm*2],nex[Maxm*2],edg[Maxm*2],Cos[Maxm*2];
int pre[Maxn],ds[Maxn],liu[Maxn];
bool inq[Maxn];
bool spfa(int s,int t)
{
	 memset(ds,inf,sizeof(ds)),memset(liu,inf,sizeof(liu)),memset(inq,false,sizeof(inq));
	 queue<int> q; q.push(s),ds[s]=0,inq[s]=true,pre[t]=-1;
	 while(!q.empty())
	 {
	 	 int cur=q.front(); q.pop(),inq[cur]=false;
	 	 for(int i=hea[cur];i;i=nex[i]) if(edg[i]>0 && ds[vis]>ds[cur]+Cos[i] && ds[cur]+Cos[i]>=0)
 	 	 {
	 	 	 liu[ver[i]]=min(liu[cur],edg[i]);
	 	 	 pre[ver[i]]=i,ds[ver[i]]=ds[cur]+Cos[i];
 	 	 	 if(!inq[ver[i]]) inq[ver[i]]=true,q.push(ver[i]);
		 }
	 }
	 return pre[t]!=-1;
}
void EK(int s,int t)
{
	 while(spfa(s,t))
	 {
	 	 int x=t;
	 	 while(x!=s)
	 	 {
	 	 	 int i=pre[x];
	 	 	 edg[i]-=liu[t],edg[i^1]+=liu[t];
	 	 	 x=ver[i^1];
		 }
		 hua+=ds[t]*liu[t];
		 sum+=liu[t];
	 }
}

EK(s,t);
printf("%d %d\n",sum,hua);

dinic（类 dinic 算法）

注意加上当前弧优化，复杂度为 \(O(nmf)\)，其中 \(f\) 为流量 。

只用将 DFS 改为 SPFA 就可以了，将记录深度的 deep 变为 distance。

\(\bigstar\texttt{important}\)：需要判断这个点在一次 dfs 中是否已经访问过了！！不然可能会无限递归。

$\texttt{code}$

struct Dinic_cost
{
    #define Maxn ?
    #define Maxm ?
    int tot=1;
    int tmphea[Maxn],hea[Maxn],nex[Maxm<<1],ver[Maxm<<1];
    ll sumflow,sumcost,edg[Maxm<<1],Cost[Maxm<<1];
    bool inq[Maxn];
    ll dis[Maxn];
    inline void init() { tot=1,memset(hea,0,sizeof(hea)); }
    inline void add_edge(int x,int y,ll d,ll c)
	 {
        ver[++tot]=y,nex[tot]=hea[x],hea[x]=tot,edg[tot]=d,Cost[tot]=c;
        ver[++tot]=x,nex[tot]=hea[y],hea[y]=tot,edg[tot]=0,Cost[tot]=-c;
    }
    inline bool spfa(int s,int t)
    {
        memset(dis,0x3f,sizeof(dis)),dis[s]=0;
        memcpy(tmphea,hea,sizeof(hea));
        queue<int> q; q.push(s);
        while(!q.empty())
        {
            int cur=q.front(); q.pop(),inq[cur]=false;
            for(int i=hea[cur];i;i=nex[i])
                if(edg[i] && dis[ver[i]]>dis[cur]+Cost[i])
                {
                    dis[ver[i]]=dis[cur]+Cost[i];
                    if(!inq[ver[i]]) q.push(ver[i]),inq[ver[i]]=true;
                }
        }
        return dis[t]!=infll;
    }
    ll dfs(int x,ll flow,int t)
    {
        if(x==t || !flow) return flow;
        ll rest=flow,tmp;
        inq[x]=true;
        for(int i=tmphea[x];i && rest;i=nex[i])
        {
            tmphea[x]=i;
            if(!inq[ver[i]] && edg[i] && dis[ver[i]]==dis[x]+Cost[i])
            {
                if(!(tmp = dfs(ver[i],min(edg[i],rest),t)))
                    dis[ver[i]]=infll;
                sumcost+=Cost[i]*tmp,edg[i]-=tmp,edg[i^1]+=tmp,rest-=tmp;
            }
        }
        inq[x]=false;
        return flow-rest;
    }
    inline pll solve(int s,int t)
    {
        sumflow=sumcost=0;
        while(spfa(s,t)) sumflow+=dfs(s,infll,t);
        return pll(sumflow,sumcost);
    }
    #undef Maxn
    #undef Maxm
}G;

费用流性质及应用

模拟费用流

（初试云雨情，只是做了一道模板题）

CF724E Goods transportation

有 \(n\) 个城市，\(1\dots n\) 编号，每个城市生产 \(p_i\) 个货物，最多可卖掉 \(s_i\) 个货物。城市之间可以从编号小的往编号大的运输货物并卖出，而且两个城市之间最多直接传送 \(c\) 个货物。求最大能卖出多少货物。\(n\le 10^4\)。

显然的网络流模型，但直接网络流不用说了肯定不行。那么网络流不能跑了，考虑最大流等于最小割。

最小割将图分为两个部分：一部分和 \(s\) 超级源点相连提供流量，一部分和 \(t\) 相连接受流量。

由于题目规定只能从编号小的向编号大的传送货物，也就是避免了后效性，考虑 DP。

设 \(dp_{i,j}\) 表示在前 \(i\) 个点中，有 \(j\) 个被划分到了 \(s\) 集合的最小割。

考虑加入一个点 \(i\)，对加入两个集合的情况分类讨论：

• 一种方案是将点划分到 \(s\)，代价是割掉流量为 \(s_i\) 的边。

• 另一种方案是将点划分到 \(t\)，代价是割掉流量为 \(p_i+c\times j\) 的边。

直接 \(n^2\) 转移可以过啦！

最小割性质及应用

前置知识：

给定一个网络 \(G=(V,E)\) ，源点和汇点为 \(S\) 和 \(T\) ，若删去边集 \(E'\subseteq E\) ，使得 \(S\) 和 \(T\) 不连通，则该边集成为网络的割。边的容量值和最小的割成为该网络的最小割。

最小割 = 最大流

平面图最小割转对偶图最短路

比如我们现在有一个 \(n\times m\) 的网格，我们需要求出这个网格的最小割，而数据范围又是 \(n,m\le 500\)，一般的网络流不能通过这样的题，因此我们需要转化为一个最短路问题。

可以选择将网格的个点区域与网格边界区域交换，即将每个个点看为一个节点，将原本的边权变为格点与格点之间的边权，之后再两侧分别建立源点和汇点，直接跑最短路即可。

P2046 [NOI2010] 海拔

这一题成功卡掉了 \(ISAP\) 做法！

再如 [CSP-S 2021] 交通规划。

最大权闭合子图问题

定义：有一个有向图，每一个点都有一个权值（可以为正或负或 \(0\)），选择一个权值和最大的子图，使得每个点的后继都在子图里面，这个子图就叫最大权闭合子图。

这个问题可以转化为最小割问题，用网络流解决。

• 从源点 \(s\) 向每个正权点连一条容量为权值的边。
• 有向图原来的边容量全部为无限大。
• 每个负权点向汇点 \(t\) 连一条容量为权值的绝对值的边。

求它的最小割，割掉后，与源点 \(s\) 连通的点构成最大权闭合子图，权值为（正权值之和 \(-\) 最小割）。

证明见 CaptainHarryChen 的博客

输出方案，分两类讨论：

• 源点流向一个正权点的边有边权：则这个点的所有后继都已经被流过了，这个点必选。

• 源点到一个点的边权为 \(0\)，但是有源点到其他的点的边权不为 \(0\)，而且这个点可以通过反边等走到那个边权为 \(0\) 的点：说明这两个点共同分担了消耗，这个点也可以选。

那么怎么求出方案呢？在 dinic 的最后一次最小割跑完的图上访问到的点就是选中的点了！

经典例题：【网络流 \(24\) 题】太空飞行计划问题，[NOI2006] 最大获利，[NOI2009] 植物大战僵尸

二选一问题

一般的二选一问题都可以转化为最小割模型，即从源点向每一个点连选集合 \(A\) 的收益，从每个点向汇点连选择集合 \(B\) 的收益。

打包选择增加收益

假设有限制条件：如果物品 \(i\) 和 \(j\) 同时选择 \(A\) 集合，将额外获得 \(w_A\) 收益；如果同时选择 \(B\) 集合，将额外获得 \(w_B\) 收益。

这是，我们可以这样建图：（来自 jun头吉吉 的洛谷博客）

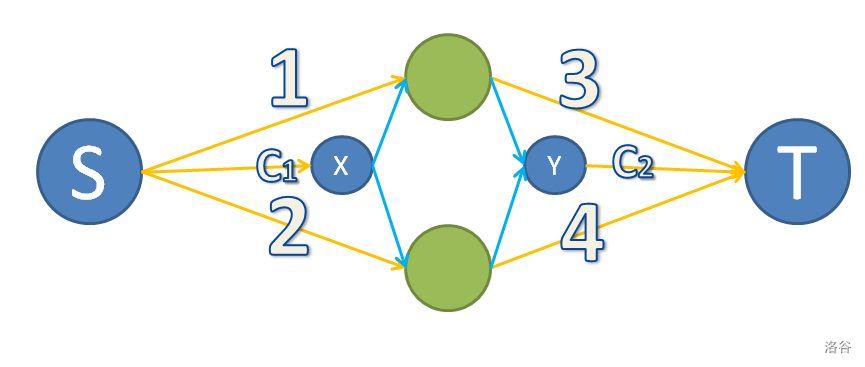
这样可以保证舍去的最少的代价，留下的流量就是最大收益了。

类似套路：P1361 小M的作物 P4313 文理分科 P1646 [国家集训队]happiness P1935 [国家集训队]圈地计划

可行边（点）必须边（点）

可以先对所有流量不为 \(0\) 的边跑一遍 Tarjan，之后快速判断连通性，比如[AHOI2009]最小割。

可行边

存在一个最小代价路径切断方案，其中该道路被切断。可行边减小多少，网络流就会减小多少。例如：

\[s\xrightarrow{1}1\xrightarrow{1}t \]

这两条边都是可行边：他们可以作为最小割，可以割左边那一条也可以割右边那一条。

判断的充要条件：

• 在最小割中流满。

• \(u,v\) 在残量网络中不连通，即不存在 \(u\rightarrow v\)，或 \(u\) 和 \(v\) 不在一个 \(SCC\) 中。

必须边

对任何一个最小代价路径切断方案，都有该道路被切断。必须边增大一些些，网络流也会增大一些些。例如：

\[s\xrightarrow{1}t \]

这里这条边就是必须边，必须割掉这条边。

判断的充要条件：

• 在最小割中流满。

• 存在 \(s\rightarrow u,v\rightarrow t\)，或 \(s\) 和 \(u\) 在一个 \(SCC\) 中且 \(v\) 和 \(t\) 在一个 \(SCC\) 中。

网络流其他常见技巧

限流拆点问题

P3191 [HNOI2007]紧急疏散EVACUATE

发现每个点单位时间内只能允许一单位的流量通过，因此我们将一个点拆成 \(t\) 个点，由 \(t\) 向 \(t+1\) 连边，每个分点向汇点流流量为 \(1\)。

这样确保每个时间内只能流过 \(1\) 单位流量。

需要连接边权为负的最小割

可以直接给网络流上每一条边加上 \(\infty_{\min}\) 的价值，当然原先需要为 \(\infty\) 的边赋为 \(\infty_{\max}\)。

记得最终答案需要减去左右可能多加的 \(\infty_{\min}\)！

网络流杂题

P6054 [RC-02] 开门大吉

首先求出每个人选择每一道题的代价，使用最小割模型解决，如此建图：

• 每个人拆为 \(m+1\) 个点，\((i,j)\rightarrow(i,j+1)\) 流量为第 \(i\) 个人选择第 \(j\) 套题的期望收益。

• 源点向 \((i,1)\) 连 \(\infty\)。

• \((i,m+1)\) 向 汇点连 \(\infty\)。

• 对于性质 \(x\) 需要比 \(y\) 大 \(k\)：\((y,p)\rightarrow(x,p+k)\) 连 \(\infty\)。

• \(\bigstar\)：为了判断无解情况，需要连 \((i,j+1)\rightarrow(i,j)\)！否则可能判断不了无解！！！

P3227 [HNOI2013]切糕 几乎一模一样！

XJOI3902B

有 \(k\) 个小朋友在公园中玩耍，公园由 \(n\) 个景点和 \(m\) 条有向路径组成。一开始 \(k\) 个小朋友分别在 \(k\) 个互不相同的景点中，但是开始每条路都是的脏的。

每次你可以选择一条路并将它打扫干净，如果在这条路的起点有小朋友，他会走到这条路的终点。

如果有两个小朋友在同一个景点相遇了，那么他们会产生一场 Battle 使得其中一个小朋友退出游戏。

要求最终将所有路径都打扫干净，并且结束后还在玩耍的小朋友数量尽可能多，请输出这个数量。

\(k\le n\le 100,m\le n\times(n-1)\)，每个小朋友的初始位置给定。

首先考虑如果这张图是一个 DAG，考虑对每个有小朋友的点，求出除了自己之外的支配集，这些点都是这个点可以最终停留的位置（如果没有出度它的支配集改为自己）。

那么其实最终保留的点的数量就是将每个小朋友和终点匹配，最大匹配数量。

考虑如果是一个无向图，一个环上只要有一个点没有人，一定可以通过旋转一整圈的方式不发生冲突；如果有人，那么只能牺牲一个人后腾出空位继续走。

那么只用将一个环缩为一个点，将它看做普通点没有人的点继续做即可。

\(\texttt{code}\)

CF1717F Madoka and The First Session

图上有 \(n\) 个点，每个点初始都为 \(0\)。有 \(m\) 条边连接 \(u_i\) 和 \(v_i\)，可以让 \(u_i\) 给 \(v_i\) 大小为 \(1\) 的权值。

要求最终选择其中一些边流过去，使得在集合 \(\{s\}\) 中的点的权值都有 \(val_i=a_i\)，其他点的权值不做要求。

\(n,m\le 10^4,|a_i|\le m\)。

那些不要求的点可以整体用 \(+\infty\) 的边连成一体，记做连通块 \(tmp\)

那么如果 \(a_i>0\)，就在 \((i,t)\) 中连接 \(a_i\) 的边，否则在 \((s,i)\) 中连接 \(-a_i\) 的边。

记录当前从 \(s\) 中连出了大小为 \(in\) 的流量，流向 \(t\) 大小 \(out\) 的流量，那么相差多少就连向 \(tmp\) 连接多少。

最终如果能够流满，则说明可行。