机器学习笔记(15)-隐马尔可夫模型(归纳总结)

机器学习笔记(15)-隐马尔可夫模型(归纳总结)

模型归纳

这一节我们再聊一聊HMM用到的算法和要解决的任务，更好地总结归纳下HMM模型或者说这一类模型的作用。首先先回顾一下HMM的模型结构：

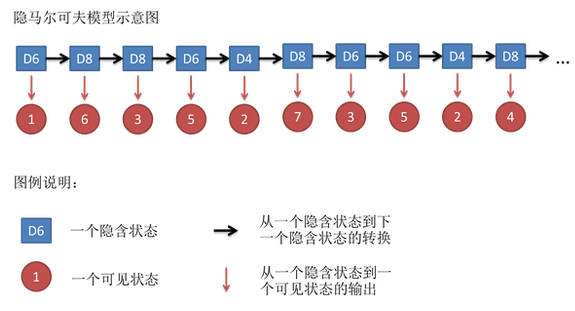
这是一个比较通用的带有隐藏状态的模型。该模型有下面几个特点：

1. 观测变量：就是我们看到的已知样本（图中红色圈）。
2. 隐藏状态：我们认为每一个观测变量是通过一个未知的隐藏状态来确定的（图中蓝色方块）。
3. 时间序列：每一个时刻的隐藏状态都和前面时刻的隐藏状态有关（隐藏状态不是独立分布的）。

上面三个特点就是我们建立模型结构的思想，其实和循环神经网络是有些类似的，甚至可以说思想是一致的，只是模型结构更加复杂，求解算法不同而已。

在HMM中，为了使模型求解计算过程变得简单，引入了两个假设：

1. 齐次马尔可夫假设：每个时刻的隐藏状态只和前一个时刻的隐藏状态有关。
2. 观测独立假设：每个观测变量之和当前时刻的隐藏变量有关。

HMM提出了三个要解决的任务，分别是：估计、学习和解码任务。其实我们可以推广到更加一般任务上，首先是两大类任务：学习任务和推断任务。

学习任务（Learning）：也就是训练模型，把模型参数估计出来。

在HMM中对应算法为：Baum Welch，也就是我们现在说的EM算法。

根据已知观测变量，求出最大似然估计，表达式为：

\[\lambda_{MLE}=\underset{\lambda}{argmax}\;P(O|\lambda) \]

推断任务（Inference）：在训练得到模型参数\(\lambda\)后，利用模型作一系列推断，解决任务：

任务一：Decoding（解码问题）

采用的算法为：维特比算法（Viterbi）

根据观测变量序列，求解最大可能的隐藏状态序列，表达式为：

\[I=\underset{I}{argmax}\;P(I|O;\lambda) \]

任务二：Evaluation（估计问题）

采用的算法为：前向算法（Forward Algorithm）或后向算法（Backward Algorithm）

通过前向或后向递推式，求得观测变量的序列概率：\(P(X;\lambda)\)

任务三：Filtering（滤波问题）

采用的算法为：前向算法（Forward Algorithm）

通过观测变量序列，求出该时刻t的隐藏状态：\(P(I_{t}|O_{1\sim t};\lambda)\)

任务四：Smoothing（平滑问题）

采用的算法为：前向-后向算法（Forward-Backward Algorithm）

通过全部的观测变量序列，求出该时刻t的隐藏状态：\(P(I_{t}|O_{1\sim T};\lambda)\)

任务五：Prediction（预测问题）

采用的算法为：前向算法（Forward Algorithm）

通过观测变量序列，预测得到t时刻之后的隐藏状态和观测变量：

\[P(O_{t+1}|O_{1\sim T};\lambda) \]

\[P(I_{t+1}|O_{1\sim T};\lambda) \]

模型举例

我们还是用自然语言处理中的序列标注任务来举例说明，HMM有些什么用处：

假如我们想要使用序列标注来作命名实体识别任务或者分类任务，也就是根据已知的段落语句，学习得到语句中每个词序列的标签。那么在HMM模型中，我们把句子看成是观测变量序列，标签看成是隐藏状态序列。

任务一解码问题就是：根据句子序列，得到标签序列。

任务二估计问题就是：得到句子的概率，也就是词或字组成一句句子的合理程度。

任务三滤波问题就是：输入一句句子序列，给它一个分类标签。

任务四平滑问题就是：输入全部的句子，给它任意的中间的隐藏状态标签。和滤波问题类似。

任务五预测问题就是：根据前t时刻的句子，预测t时刻后的句子或标签。比如用来作段落生成等。

虽然神经网络出现后，这类模型在使用的地位就下降了，但是模型的思想都是类似的，循环神经网络的发展也是借助该思想一步一步发展和完善的。