机器学习笔记(14)-隐马尔可夫模型
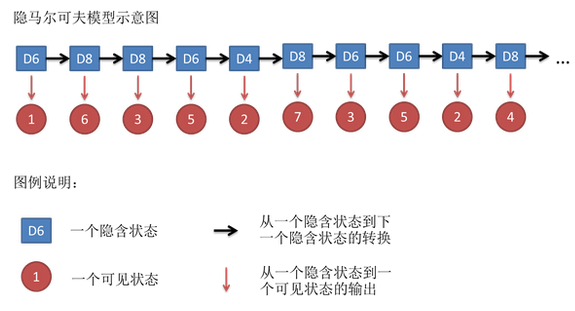
隐马尔可夫模型(Hidden Markov Model,HMM)属于概率图模型,在深度学习尤其是循环神经网络火热之前,在处理自然语言nlp任务时是非常流行的模型。模型结构和时间序列有关,是一种动态模型,即样本与样本之间并非独立分布的,而是相互关联。
动态模型的思想是:我们把已知样本看成是观测变量,认为每个观测变量的出现都是依赖于一个隐藏状态。比如之前讲到的高斯混合模型(GMM),每个观测变量\(x\)依赖于一个隐藏状态\(z\),\(x\)是在\(z\)条件下服从正太分布。而HMM是时间序列模型,每个隐藏状态\(z\)有依赖关系,后面的\(z_{n}\)依赖于前面的隐藏状态\(z_{1}\sim z_{n-1}\),如下图:
![]()
而对于隐藏状态,我们又分为:离散:HMM,连续(线性):卡尔曼滤波(Kalman Filter),连续(非线性):粒子滤波(Particle Filter)。下面我们主要来介绍离散型HMM。
HMM三个任务
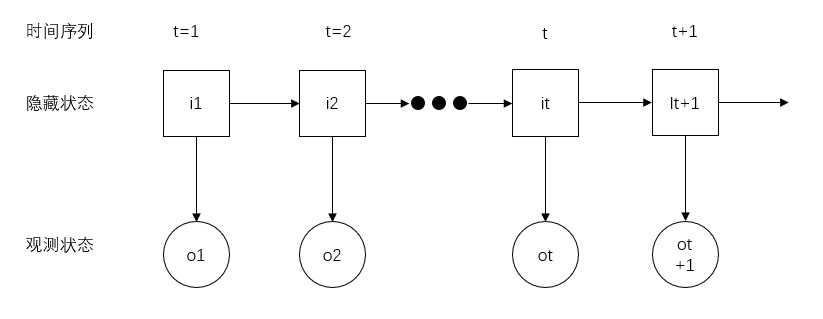
之前我们对HMM进行了一个基本的介绍,下面就采用数学符号形式来表达HMM:
![]()
- t表示时间序列;
- 隐藏状态序列:\(i_{1},i_{2},\cdots,i_{t},\cdots\);
- 隐藏状态的N个可能值:\(Q=\{q_{1},q_{2},\cdots,q_{n}\}\);
- 观测变量序列:\(o_{1},o_{2},\cdots,o_{t},\cdots\);
- 观测变量的M个可能值:\(V=\{v_{1},v_{2},\cdots,v_{m}\}\);
- 模型参数:\(\lambda=(\pi,A,B)\),其中\(\pi\)是初始状态分布;
- \(A\)是状态转移矩阵,即\(q_{i}\)到\(Q\)中每个状态值互相之间的概率,记为\(a_{st}=P(i_{t+1}=q_{t}|i_{t}=q_{s})\),或者记为\(a_{i_{t}i_{t+1}}=P(i_{t+1}=q_{t}|i_{t}=q_{s})\);
- \(B\)是发射概率矩阵,即\(Q\)到\(V\)中每个隐藏状态生成观测变量的概率,记为\(b_{i}(o_{t})=P(o_{t}=v_{k}|i_{t}=q_{i})\),或者记为\(b_{i_{t}o_{t}}=P(o_{t}=v_{k}|i_{t}=q_{i})\)。
HMM两个基本假设,用于简化模型:
1.齐次马尔可夫假设:每个隐藏状态\(i_{t+1}\)只和前一个隐藏状态\(i_{t}\)有关,和其他隐藏状态无关;
\[P(i_{t+1}|i_{t},i_{t-1},\cdots,i_{1},o_{t+1},o_{t},\cdots,o_{1})=P(i_{t+1}|i_{t})
\]
2.观测独立假设:每个t时刻的观测变量之和该时刻的隐藏状态有关。
\[P(o_{t}|i_{t},i_{t-1},\cdots,i_{1},o_{t-1},o_{t-2},\cdots,o_{1})=P(o_{t}|i_{t})
\]
HMM要解决的三个任务:
- 估计(Evaluation):已知模型参数\(\lambda\),求观测序列的概率\(P(O|\lambda)\);
- 学习(Learning):已知观测序列,求模型参数\(\lambda\),使观测序列的出现概率最大\(argmax\;P(O|\lambda)\);
- 解码(Decoding):已知观测序列,求最大概率隐藏状态序列\(P(I|O)\)
估计问题,我们采用前向、后向算法;学习问题,采用Baum Welch算法,也就是后面所说的EM算法;解码问题,我们采用维特比(Vertib)。
所以HMM的核心是:一个模型\(\lambda=(\pi,A,B)\),两个假设,三个任务。也是我们掌握HMM算法的关键所在。
比如我们在序列标注任务时,我们训练模型得到模型参数\(\lambda\),然后通过解码,根据已知观测变量,获得隐藏状态序列,比如已知词序列,获得标注结果。
前向后向算法
我们现来看我们的第一个任务,估计任务。当已知模型参数\(\lambda=(\pi,A,B)\)时,求\(P(O|\lambda)\)
根据边缘概率分布,得到:
\[\begin{aligned}
P(O|\lambda)
&=\sum_{I}^{}P(O,I;\lambda)\\
&=\sum_{I}^{}P(O|I;\lambda)\cdot P(I|\lambda)
\end{aligned}
\]
上式中的两项\(P(O|I;\lambda)\)和\(P(I|\lambda)\)我们分开来看:
首先根据观测独立假设,t时刻观测变量只和该时刻的隐藏状态有关,所以:
\[\begin{aligned}
P(O|I;\lambda)
&=p(o_{1}|i_{1};\lambda)\cdot p(o_{2}|i_{2};\lambda)\cdot \cdots \cdot p(o_{t}|i_{t};\lambda)\\
&=\prod_{t=1}^{T}p(o_{t}|i_{t};\lambda)\\
&=\prod_{t=1}^{T}b_{i_{t}o_{t}}
\end{aligned}
\]
然后把\(P(I|\lambda)\)展开:
\[\begin{aligned}
P(I|\lambda)
&=P(i_{1},i_{2},\cdots,i_{t};\lambda)\\
&=P(i_{t}|i_{1},i_{2},\cdots,i_{t-1};\lambda)\cdot P(i_{1},i_{2},\cdots,i_{t-1};\lambda)\\
&=P(i_{t}|i_{t-1};\lambda)\cdot P(i_{t-1}|i_{1},i_{2},\cdots,i_{t-2};\lambda)\cdot P(i_{1},i_{2},\cdots,i_{t-2};\lambda)\\
\vdots \\
&=P(i_{t}|i_{t-1};\lambda)\cdot P(i_{t-1}|i_{t-2};\lambda)\cdot \cdots \cdot P(i_{2}|i_{1};\lambda)\cdot P(i_{1};\lambda)\\
&=\prod_{t=2}^{T}p(i_{t}|i_{t-1};\lambda)\cdot p(i_{1};\lambda)\\
&=\prod_{t=2}^{T}a_{i_{t-1}i_{t}}\cdot \pi_{i_{1}}
\end{aligned}
\]
上式中间是一个利用概率分解方法递归依次展开,最后根据齐次马尔可夫假设和初始概率矩阵化简得到。
把两个结果代入到\(P(O|\lambda)\):
\[\begin{aligned}
P(O|\lambda)
&=\sum_{I}^{}P(O|I;\lambda)\cdot P(I|\lambda)\\
&=\sum_{I}^{}[\prod_{t=1}^{T}b_{i_{t}o_{t}}\prod_{t=2}^{T}a_{i_{t-1}i_{t}}\cdot \pi_{i_{1}}]
\end{aligned}
\]
上式就是我们要的结果,但是上面这个式子我们根本就没有办法来计算,\(\sum_{I}^{}\)的计算代价为\(O(N^T)\),计算量太大了,隐藏状态值的数量N的T时间序列长度次方。因此引入我们要介绍的前向后向算法。我们详细介绍下前向算法,后向算法和前向算法类似,都是通过求出递归表达式来求解。
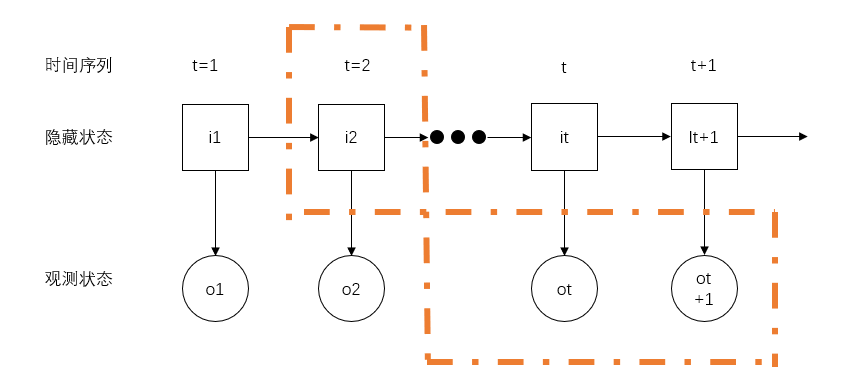
前向算法的思路是:把t时刻的隐藏状态和从1时刻开始到该时刻的观测变量看成一个整体,如下图:
![]()
我们把这块区域记为:
\[\begin{aligned}
\beta _{t}(s)=P(O_{1\sim t},i_{t}=q_{s};\lambda)
\end{aligned}
\]
这里隐藏状态的值固定,从全部的时间序列T来看,用T来表示时间序列最后一个时刻,就是:
\[\begin{aligned}
\beta _{T}(s)=P(O,i_{t}=q_{s};\lambda)
\end{aligned}
\]
进一步通过边缘概率求积分(离散求和),我们来表示\(P(O|\lambda)\):
\[\begin{aligned}
P(O|\lambda)
&=\sum_{s=1}^{N}P(O,i_{t}=q_{s};\lambda)\\
&=\sum_{s=1}^{N}\beta _{T}(s)
\end{aligned}
\]
如果\(\beta _{t}(s)\)和\(\beta _{t-1}(t)\)有关系,那么我们就可以通过递归的方式求出最后一个时刻\(\beta _{T}(s)\):
\[\begin{aligned}
\beta _{t}(s)
&=P(O_{1\sim t},i_{t}=q_{s};\lambda)\\
&=\sum_{s=1}^{N}P(O_{1\sim t},i_{t}=q_{s},i_{t-1}=q_{t};\lambda)\\
&=\sum_{s=1}^{N}[P(o_{t}=q_{s}|O_{1\sim t-1},i_{t}=q_{s},i_{t-1}=q_{t};\lambda)\cdot P(O_{1\sim t-1},i_{t}=q_{s},i_{t-1}=q_{t};\lambda)]\\
&=\sum_{s=1}^{N}[P(o_{t}|i_{t}=q_{s};\lambda)\cdot P(i_{t}=q_{s}|O_{1\sim t-1},i_{t-1}=q_{t};\lambda)\cdot P(O_{1\sim t-1},i_{t-1}=q_{t};\lambda)]\\
&=\sum_{s=1}^{N}[P(o_{t}|i_{t}=q_{s};\lambda)\cdot P(i_{t}=q_{s}|i_{t-1}=q_{t};\lambda)\cdot P(O_{1\sim t-1},i_{t-1}=q_{t};\lambda)]\\
&=\sum_{s=1}^{N}[b_{s}(o_{t})\cdot a_{ts}\cdot \beta _{t-1}(t)]
\end{aligned}
\]
上式的推导过程就是利用HMM的两个假设,最后形成了 递归的形式,从而求得\(P(O|\lambda)\)
后向算法和前向的算法的思路基本一致,只不过看的整体不同而已:
![]()
这里就不推导了,因为前向后向算法的作用是一致的,只不过一个是从前往后推,另一个是从后往前推而已。最后都是通过递归式得到我们的\(P(O|\lambda)\)。
Baum Welch算法
该算法也就是我们所说的EM算法,只不过在提出该算法时,EM算法还没有诞生,思想本质是完全一致的。
提出该算法的目的是为了解决HMM的第二个任务,根据已知观测变量,求出模型参数\(\lambda=(\pi,A,B)\)。
我们先回顾一下EM算法中的表达式(不记得的同学可以看【机器学习笔记(9)EM算法】),如何一步一步迭代得到收敛的模型参数的:
\[\theta^{t+1}=\underset{\theta}{argmax}\;\int_{Z}^{}P(Z|X;\theta^t)\log P(X,Z|\theta)d_{Z}
\]
该迭代优化函数中,\(\theta\)是我们的模型参数,\(Z\)是隐藏状态,\(X\)是观测变量。我们采用HMM的定义表示形式:
\[\begin{aligned}
\theta&\rightarrow \lambda\\
Z&\rightarrow I\\
X&\rightarrow O
\end{aligned}
\]
\[\begin{aligned}
\lambda^{t+1}
&=\underset{\lambda}{argmax}\;Q(\lambda,\lambda^{t})\\
&=\underset{\lambda}{argmax}\;\sum_{I}^{}P(I|O;\lambda^t)\log P(O,I|\lambda)
\end{aligned}
\]
还记得我们之前在前向后向算法前推导的函数:
\[\begin{aligned}
P(O|\lambda)
&=\sum_{I}^{}P(O|I;\lambda)\cdot P(I|\lambda)\\
&=\sum_{I}^{}[\prod_{t=1}^{T}b_{i_{t}o_{t}}\prod_{t=2}^{T}a_{i_{t-1}i_{t}}\cdot \pi_{i_{1}}]
\end{aligned}
\]
我们上式代入到\(\log P(O,I|\lambda)\)中:
\[\begin{aligned}
Q(\lambda,\lambda^{t})
&=\sum_{I}^{}P(I|O;\lambda^t)\log P(O,I|\lambda)\\
&=\sum_{I}^{}[P(I|O;\lambda^t)\cdot (\sum_{t=1}^{T}\log b_{i_{t}o_{t}}+\sum_{t=2}^{T}\log a_{i_{t-1}i_{t}}+\log \pi_{i_{1}})]
\end{aligned}
\]
我们先求\(\pi^{(t+1)}\),事实上\(\lambda^{(t+1)}=(\pi^{(t+1)},A^{(t+1)},B^{(t+1)})\)中求三个参数的方式都差不多,代入就有:
\[\begin{aligned}
\pi^{(t+1)}
&=\underset{\pi}{argmax}\;Q(\pi,\pi^{(t)})\\
&=\underset{\pi}{argmax}\;\sum_{I}^{}[P(I|O;\lambda^t)\cdot (\sum_{t=1}^{T}\log b_{i_{t}o_{t}}+\sum_{t=2}^{T}\log a_{i_{t-1}i_{t}}+\log \pi_{i_{1}})]\\
&=\underset{\pi}{argmax}\;\sum_{I}^{}[P(I|O;\lambda^t)\cdot \log \pi_{i_{1}}]\\
\end{aligned}
\]
我们先观察上式中的\(P(I|O;\lambda^t)\),根据贝叶斯公式有:
\[P(I|O;\lambda^t)=\frac{P(I,O;\lambda^t)}{P(O|\lambda^t)}
\]
由于\(\underset{\pi}{argmax}\;P(O|\lambda^t)\)在是没有关系的,因为\(\lambda^t\)是上一个迭代的结果,是常数,所以分母可以忽略:
\[\begin{aligned}
\pi^{(t+1)}
&=\underset{\pi}{argmax}\;\sum_{I}^{}[P(I,O;\lambda^t)\cdot \log \pi_{i_{1}}]\\
&=\underset{\pi}{argmax}\;\sum_{i_{1}}^{}[P(O,i_{1};\lambda^t)\cdot \log \pi_{i_{1}}]\\
&=\underset{\pi}{argmax}\;\sum_{s=1}^{N}[P(O,i_{1}=q_{s};\lambda^t)\cdot \log \pi_{s}]
\end{aligned}
\]
上式中的第二步化简是通过边缘概率积分为1得到的。其实我们应该得到的是一个带约束的表达式:
\[\begin{aligned}
\left\{\begin{matrix}
\pi^{(t+1)}=\underset{\pi}{argmax}\;\sum_{s=1}^{N}[P(O,i_{1}=q_{s};\lambda^t)\cdot \log \pi_{s}]\\
s.t.\;\sum_{i=1}^{N}\pi_{i}=1
\end{matrix}\right.
\end{aligned}
\]
要求解上式,我们可以采用拉格朗日乘子法来解:
\[\begin{aligned}
\left\{\begin{matrix}
\mathcal{L}(\pi,\eta)=\sum_{s=1}^{N}[P(O,i_{1}=q_{s};\lambda^t)\cdot \log \pi_{s}]+\eta(\sum_{i=1}^{N}\pi_{i}-1)\\
s.t.\;\eta\geqslant 0
\end{matrix}\right.
\end{aligned}
\]
我们对\(\pi\)求偏导:
\[\begin{aligned}
\frac{\partial \mathcal{L}(\pi,\eta)}{\partial \pi_{s}}
&=\frac{1}{\pi_{s}}P(O,i_{1}=q_{s};\lambda^t)+\eta\\
&=0
\end{aligned}
\]
两边加上\(\sum_{i=1}^{N}\):
\[\begin{aligned}
\sum_{i=1}^{N}P(O,i_{1}=q_{s};\lambda^t)+\sum_{i=1}^{N}\pi_{s}\eta=0\\
P(O|\lambda^t)+\eta=0
\end{aligned}
\]
\[\eta=-P(O|\lambda^t)
\]
把\(\eta\)代入:
\[\pi^{(t+1)}=\frac{P(O,i_{1}=q_{s};\lambda^t)}{P(O|\lambda^t)}
\]
这样我们就可以根据上一次迭代的结果,得到这一次的模型参数了。只要同样把\(A^{(t+1)}\)和\(B^{(t+1)}\)都解出来,反复EM把收敛的模型参数\(\lambda^{(t+1)}=(\pi^{(t+1)},A^{(t+1)},B^{(t+1)})\)得到就行了。
解码(Viterbi)
HMM是采用Viterbi算法来进行解码的,在得到我们的模型参数\(\lambda=(\pi,A,B)\)后,计算\(P(I|O;\lambda)\)。
思想就是求最大概率的隐藏状态序列,我们用数学表达式来表示就是:
令
\[\xi _{t}(s)=\underset{i_{1\sim t-1}}{max}\;P(O_{1\sim t},I_{1\sim t-1},i_{t}=q_{s})
\]
其中初始值:
\[\xi _{1}(s)=P(o_{1},i_{1}=q_{s})=1
\]
得到递推式:
\[\begin{aligned}
\xi _{t+1}(j)
&=\underset{i_{1\sim t}}{max}\;P(O_{1\sim t+1},I_{1\sim t},i_{t+1}=q_{j})\\
&=\underset{1\le s\le N}{max}\;\xi _{t}(s)\cdot a_{sj}\cdot b_{j}(o_{t+1})
\end{aligned}
\]
定义上一个隐藏状态的值:
\[\varphi_{t+1}(j)=\underset{1\le s\le N}{argmax}\;\xi _{t}(s)\cdot a_{sj}
\]



 浙公网安备 33010602011771号
浙公网安备 33010602011771号