机器学习笔记(12)-决策树

机器学习笔记(12)-决策树

决策树（Decision Tree，DT）是一个使用相当广泛的树模型机器学习算法，也是很多算法如随机森林、xgboost等的基础算法，这一节主要探究下该算法的基本原理。

决策树的介绍主要从以下几点来讲解：

1. 决策树的基本构建流程
2. 分支划分算法
3. 剪枝处理

基本构建流程

假设数据集为：

1. 数据集\(D=\{(x_{1},y_{1}),(x_{2},y_{2}),\cdots,(x_{n},y_{n})\}\)，
2. 属性集A=\(\{a_{1},a_{2},\cdots,a_{p}\}\)其中每个数据样本\(x_{i}\)有p个属性

构建流程：

生成根节点；

1、从样本属性集\(A\)中选择最优划分属性\(a^*\)；

2、根据属性\(a^*\)中的属性值划分叶子节点，将数据集\(D\)划分到叶节点上；

3、重复步骤1和2，直到达到最大树深度或者叶子节点样本全部属于同一类别

可以看到构建树的流程其实是一个递归过程，而选择最优划分属性就是“分支划分算法”要解决的事情，通过上述步骤，我们的决策树就构建完成了，非常简单。下图就是一个构建决策树的例子，但是决策树不一定是一个二叉树。当离散的属性的值大于2个时，会出现多个节点。

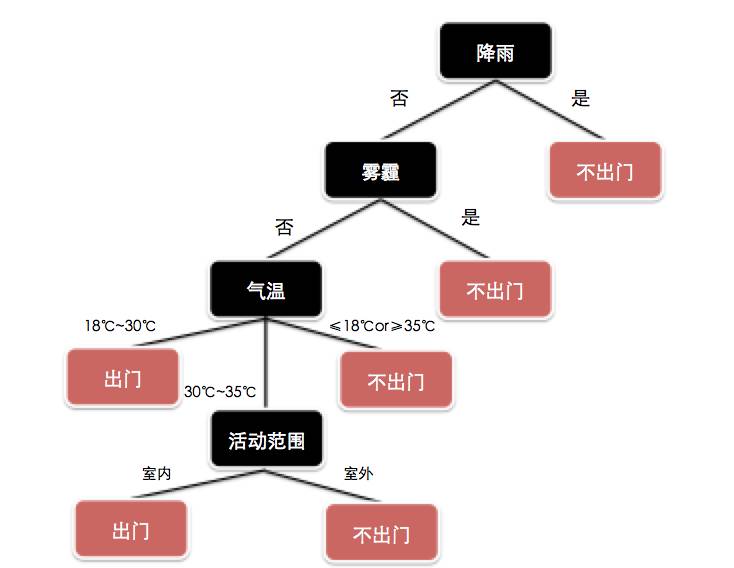
分支划分算法

分支划分算法是决策树的关键所在，主要有以下几种：

1. 信息增益（ID3）
2. 信息增益率（C4.5）
3. 基尼指数（GINI，Cart算法）

信息增益（ID3）

首先引出一个概念叫做信息熵（Information Entropy，Ent），表示事物包含的信息大小，物理学上指描述一个事物的混乱程度。通俗的说就是一个事物，如果它的属性值越多，则包含的信息越丰富，信息熵越大。

假设数据集\(D\)中有k个类别，则：

\[Ent(D)=-\sum_{k=1}^{K}p_{k}\log_{2} p_{k} \]

信息增益计算公式如下：

\[Gain(D,a)=Ent(D)-\sum_{V=1}^{V}\frac{|D^v|}{|D|}Ent(D^v) \]

其中，\(V\)表示当选定属性\(a\)时，样本中属性\(a\)上总共有\(V\)个值\(\{a^1,a^2,\cdots,a^v\}\)，\(D^v\)表示样本\(D\)上是属性\(a=a^v\)的样本个数。

接下来，我们希望当我们的决策树能够随着属性\(a\)的划分后，信息增益越大，即：

\[a^*=\underset{a\in A}{argmax}\;Gain(D,a) \]

ID3算法的思想就是我们计算所有的属性下的信息增益\(Gain(D,a)\)，从中选出最大的一个增益作为划分构成树的分枝，接下来不断重复该操作形成树。

信息增益率（C4.5）

ID3算法虽然表面上看没什么问题，但是观察\(Gain(D,a)\)公式可以发现，若\(Ent(D^v)\)都是0，即数据样本中某个属性下的值的种类越大，V越丰富，则信息增益就越大，等于信息熵。一个极端的例子就是样本的编号，代入公式必然有\(Gain(D,a)=Ent(D)\)，但是这显然是不合理的，我们不可能根据编号来作分类，没有任何意义。

而C4.5就是解决这个问题的改进版本，公式如下：

\[Gain\_ratio(D,a)=\frac{Gain(D,a)}{IV(a)} \]

其中

\[IV(a)=-\sum_{v=1}^{V}\frac{|D^v|}{|D|}\log_{2} \frac{|D^v|}{|D|} \]

上式其实就是对信息增益作了一个惩罚项，而如果属性a下的值的个数越大，则\(IV(a)\)就会越大。这样我们的信息增益率可以适当降低这个问题。但是有一点要注意，当采用C4.5算法分枝时，决策树并不是直接选取信息增益率最高的属性作为划分属性，而是先根据信息增益，从所有属性中找到信息增益高于平均的候选属性，在从这些候选属性中重新根据信息增益率选择最高的那个属性。

基尼指数（GINI）

CART决策树（分类回归树）使用基尼指数来选择划分属性，可以理解为是决策树的一个子类。公式如下：

\[Gini(D)=1-\sum_{k=1}^{K}p_{k}^2 \]

该式可以理解为从数据集\(D\)中随机抽取两个样本，其类别不一致的概率。\(Gini(D)\)越大，代表回归树的信息量越多（类似于信息熵越大）。接下来定义基尼指数为：

\[Gini\_index(D,a)=\sum_{V=1}^{V}\frac{|D^v|}{|D|}Gini(D^v) \]

然后我们选择基尼指数最小的属性作为划分分枝属性，即：

\[a^*=\underset{a\in A}{argmin}\;Gini\_index(D,a) \]

剪枝处理

剪枝处理是对决策树过拟合时，用来提升其泛化能力的手段，分为两种：预剪枝和后剪枝。

预剪枝

预剪枝是在决策树训练的时候采用的手段，即当采用分枝算法划分时，如果划分后的叶子节点能够提升分类泛化能力则分枝，否则就不根据属性分枝。

那么什么叫做能够提升泛化能力呢？

我们在训练决策树模型时，往往除了提供训练样本，同时还需要提供验证样本来评估模型的好坏，分类精度。所以预剪枝就是利用验证样本来观察该不该分枝划分。

当分枝划分后，该模型在验证集上的准确率低于训练样本的准确率时，则停止划分。举个例子，有100个人，当天气为“雾霾”时，类别为“不出门”，在训练集中，雾霾不出门有70%，而验证集中只有50%较低，则该属性“雾霾”不分枝。

预剪枝的思想很简单，就是原先的分枝在验证集上效果不会提高，那就剪枝，使得模型的复杂度降低。当然这种操作有可能会引起欠拟合。

后剪枝

后剪枝是在模型训练结束后再开始剪枝，从叶子节点开始，自底向上。剪枝原理和预剪枝一样，都是比较剪枝前后的泛化能力是否增强，但是一般后剪枝不像预剪枝会剪掉更多的叶子节点，因为预剪枝在训练时很有可能从枝干开始剪，这使得后剪枝在提高泛化能力时，相对比预剪枝产生的欠拟合风险小一些。但是相对的会提高计算量。

总结

决策树是一个非常简单的算法，它的准确率往往比我们熟知的分类模型都要低，但是决策树模型作为树模型的思想在随机森林和xgoost中都有继承和改进，使得这些模型的准确率非常高。这里对该模型进行介绍可以更好的为之后xgboost的介绍作一个铺垫。