机器学习笔记(8)-对偶关系和KKT条件
之前介绍了支持向量机SVM硬间隔和软间隔的推导过程,不熟悉的小伙伴可以查看《机器学习笔记(7)支持向量机》的内容,但是在求解中我们默认了强对偶关系和KKT条件,这一节就来理解并证明描述下。
对偶关系
先来看下结论,当满足对偶关系时,默认是符合弱对偶关系的,当满足强对偶关系时,不等式取等号,我们现来用一般形式给出原问题:
\[\begin{aligned}
\left\{\begin{matrix}
\underset{\theta}{min}\;f(\theta)\\
s.t.\;m_{i}(\theta)\leq 0,\;i=1,2,\cdots ,m\\
s.t.\;n_{j}(\theta)=0,\;j=1,2,\cdots ,n
\end{matrix}\right.
\end{aligned}
\]
接下来我们采用拉格朗日乘子法将带参数约束问题转化为不带参数约束的问题:
\[\mathcal{L}(\theta,\lambda,\eta)=f(\theta)+\sum_{i=1}^{n}\lambda_{i}m_{i}+\sum_{j=1}^{m}\eta_{i}n_{j}(\theta)
\]
代入得到:
\[\begin{aligned}
\left\{\begin{matrix}
\underset{\theta}{min}\;\underset{\lambda,\eta}{max}\;\mathcal{L}(\theta,\lambda,\eta)\\
s.t.\;\lambda_{i}\geq 0\;i=1,2,\cdots ,n
\end{matrix}\right.
\end{aligned}
\]
拉格朗日乘子法的证明我们在SVM的推导中已经讲过了
弱对偶关系证明
接下来我们先证明弱对偶关系:
\[\begin{equation}
\underset{\theta}{min}\;\underset{\lambda,\eta}{max}\;\mathcal{L}(\theta,\lambda,\eta)\geq \underset{\lambda,\eta}{max}\;\underset{\theta}{min}\;\mathcal{L}(\theta,\lambda,\eta)
\end{equation}\tag{1}
\]
证明:
首先我们借助中间变量\(\mathcal{L}(\theta,\lambda,\eta)\)得到下式:
\[\begin{aligned}
\underset{\lambda,\eta}{max}\;\mathcal{L}(\theta,\lambda,\eta)
\geq
\mathcal{L}(\theta,\lambda,\eta)
\geq
\underset{\theta}{min}\;\mathcal{L}(\theta,\lambda,\eta)
\end{aligned}
\]
左半边确定了\(\lambda,\eta\)后,我们令:
\[u(\theta)=\underset{\lambda,\eta}{max}\;\mathcal{L}(\theta,\lambda,\eta)
\]
右半边同理得到:
\[v(\lambda,\eta)=\underset{\theta}{min}\;\mathcal{L}(\theta,\lambda,\eta)
\]
于是代入公式\((1)\):
\[u(\theta)\geq v(\lambda,\eta)
\]
上式无论各自的参数怎么取,都恒成立,于是得到:
\[\underset{\theta}{min}\;u(\theta)\geq \underset{\lambda,\eta}{max}\;v(\lambda,\eta)
\]
我们把\(u(\theta),v(\lambda,\eta)\)还原回去就证明了弱对偶关系。
几何解释对偶关系
我们先用几何解释来解释下弱对偶关系,再引出强对偶关系。先观察原问题:
\[\begin{aligned}
\left\{\begin{matrix}
\underset{\theta}{min}\;f(\theta)\\
s.t.\;m_{i}(\theta)\leq 0,\;i=1,2,\cdots ,n
\end{matrix}\right.
\end{aligned}
\]
在原问题的条件下,我们令最优解为:\(p^*=\underset{\theta}{min}\;f(\theta)\)
\[\mathcal{L}(\theta,\lambda)=f(\theta)+\sum_{i=1}^{n}\lambda_{i}m_{i}
\]
\[\begin{aligned}
\left\{\begin{matrix}
\underset{\theta}{min}\;\underset{\lambda}{max}\;\mathcal{L}(\theta,\lambda)\\
s.t.\;\lambda_{i}\geq 0\;i=1,2,\cdots ,n
\end{matrix}\right.
\end{aligned}
\]
对上式对偶后,我们令对偶后的最优解为:\(d^*=\underset{\lambda}{max}\;\underset{\theta}{min}\;\mathcal{L}(\theta,\lambda)\)
于是我们要在几何上尝试证明:
\[p^* \geq d^*
\]
我们令:
\[t=f(\theta)\\
u=m_{i}(\theta),\;i=1,2,\cdots ,m
\]
假设有区域G,使得\(G=\{(u,t)\}\),根据一般情况,那么G是一个非凸区域。
我们同样将\(p^*,d^*\)表示为几何形式:
\[\begin{aligned}
p^*&=\inf \{t|u\leq 0 \}\\
d^*&=\underset{\lambda}{max}\;\underset{\theta}{min}\;(\lambda u+t)\\
&=\underset{\lambda}{max}\;\inf \{\lambda u+t|(u,t)\in G\}
\end{aligned}
\]
于是我们在几何上可以这么描述:
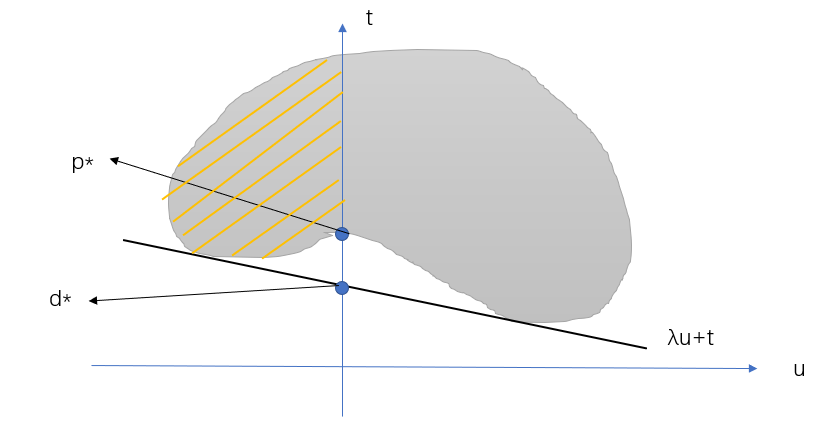
由于\(u\leq 0\),所以\(p^*\)只能取图中的黄色区域的下确界的点,\(d^*\)的最优解在图上就是与G相切的直线,并且因为\(\lambda \geq 0\)的,所以斜率是如图所示的直线。所以在非凸函数上,一定是\(p^*>d^*\)的。
那当满足\(p^*=d^*\)时,一定得是凸函数,但并非所有的凸函数都可以,还需要满足其他条件。

当上图这种形式,就是满足强对偶关系,使得\(p^*=d^*\)。
KKT条件
上一节说了,当我们满足强对偶关系时,KKT条件时它的充分必要条件,即一定能得到KKT条件。
KKT条件简单来说就是三点:
- 约束条件
- 松弛互补条件
- 梯度为0
第一点不用证明,是原问题的条件,我们主要证明松弛互补条件和梯度为0两点。
和之前一样先给出一般形式原问题:
\[\begin{aligned}\left\{\begin{matrix} \underset{\theta}{min}\;f(\theta)\\s.t.\;m_{i}(\theta)\leq 0,\;i=1,2,\cdots ,m\\
s.t.\;n_{j}(\theta)=0,\;j=1,2,\cdots ,n\end{matrix}\right.\end{aligned}
\]
接下来我们采用拉格朗日乘子法将带参数约束问题转化为不带参数约束的问题:
\[\mathcal{L}(\theta,\lambda,\eta)=f(\theta)+\sum_{i=1}^{n}\lambda_{i}m_{i}+\sum_{j=1}^{m}\eta_{i}n_{j}(\theta)
\]
代入得到:
\[\begin{aligned}\left\{\begin{matrix} \underset{\theta}{min}\;\underset{\lambda,\eta}{max}\;\mathcal{L}(\theta,\lambda,\eta)\\s.t.\;\lambda_{i}\geq 0\;i=1,2,\cdots ,n\end{matrix}\right.\end{aligned}
\]
于是我们得到:
\[p^*=\underset{\theta}{min}\;f(\theta)\\
d^*=\underset{\lambda,\eta}{max}\;\underset{\theta}{min}\;\mathcal{L}(\theta,\lambda,\eta)
\]
根据强对偶关系得到下面关系式:
\[\begin{aligned}
d^*&=\underset{\lambda,\eta}{max}\;\underset{\theta}{min}\;\mathcal{L}(\theta,\lambda,\eta)\\
&=\underset{\theta}{min}\;\mathcal{L}(\theta,\lambda^*,\eta^*)\\
&\leq \mathcal{L}(\theta^*,\lambda^*,\eta^*)\\
&=f(\theta^*)+\sum_{i=1}^{n}\lambda_{i}m_{i}+\sum_{j=1}^{m}\eta_{i}n_{j}(\theta)\\
&\leq f(\theta^*)\\
&=p^*
\end{aligned}
\]
先看松弛互补条件,因为是强对偶关系,所以取等号:
\[f(\theta^*)=f(\theta^*)+\sum_{i=1}^{n}\lambda_{i}m_{i}+\sum_{j=1}^{m}\eta_{i}n_{j}(\theta)
\]
根据初始条件:\(n_{j}(\theta)=0,\lambda \geq 0,m_{i}\leq 0\),所以要使上式成立,必须有:
\[\sum_{i=1}^{n}\lambda_{i}m_{i}=0\\
\lambda_{i}m_{i}=0,i=1,2,\cdots ,n
\]
上式就是松弛互补条件,我们接着往上看梯度为0,同样取等号:
\[\underset{\theta}{min}\;\mathcal{L}(\theta,\lambda^*,\eta^*)=\mathcal{L}(\theta^*,\lambda^*,\eta^*)\\
\]
那么必须有:
\[\frac{\partial \mathcal{L}(\theta,\lambda^*,\eta^*)}{\partial \theta}=0|_{\theta=\theta^*}
\]
这也就对应了我们SVM中的5个KKT条件。






