机器学习笔记(5)-线性分类
概述
在机器学习领域,分类的目标是指将具有相似特征的对象聚集。而一个线性分类器则透过特征的线性组合来做出分类决定,以达到此种目的。对象的特征通常被描述为特征值,而在向量中则描述为特征向量。
说人话就是在一个数据样本点上,能否找到一个线性组合来把样本点根据类别进行划分。

上图就是一个线性分类器,把两个类别的数据分在各自两边。
线性分类的体系结构:
- 硬输出:将结果映射到\(\{0,1\}\),代表算法有感知机、线性判别分析等。
- 软输出:将结果映射到\((0,1)\)的概率上,而软输出又可以分为:
- 判别式:逻辑回归(Logistics Regression,LR)
- 生成式:高斯判别分析(Gaussian Distribution Analysis,GDA)、朴素贝叶斯(Naive Bayes,NB)
感知机
感知机的核心思想是通过错误来驱动调整模型参数,比如SGD(随机梯度下降),通过梯度方向乘以一个很小的学习率,一点一点的纠正初始模型参数。
模型:
\[\begin{aligned}
y=sign(w^Tx),x\in \mathbb{R}^p,w\in \mathbb{R}^p\\
sign(x)=\left\{\begin{matrix}
1,&(x\geqslant 0))\\
-1,&(x<0)
\end{matrix}\right.
\end{aligned}
\]
选取损失函数时,一种比较直观的思想就是我分类错误的个数,我们采用\(L(w)=count(y_{i}w^Tx_{i}<0)\)来表示,但是很明显,随着参数\(w\)的偏移,\(L(w)\)不是一个连续函数,这就使得该函数不可导,我们需要选择一个可导的损失函数,最好是个正数,这样我们可以求极小值。所以我们直接采用\(-y_{i}w^Tx_{i}\)
\[L(w)=\sum_{i=1}^{n}-y_{i}w^Tx_{i}
\]
通过梯度优化就得到:
\[\begin{aligned}
\triangledown w=\sum_{i=1}^{n}-y_{i}x_{i}
\end{aligned}
\]
得到参数\(w\)的值,其中\(\alpha\)是学习率:
\[w\leftarrow w-\alpha\triangledown w
\]
线性判别分析
线性判别分析我们就只介绍下它的思想,它对于损失函数的思想是针对两个不同的类别,要求类内的样本点距离小,而类间的样本点距离大。
假设有两个类别的数据:
\[X_{c1}=(x_{c1_{1}},x_{c1_{2}},\cdots ,x_{c1_{n1}}),X_{c2}=(x_{c2_{1}},x_{c2_{2}},\cdots ,x_{c2_{n2}})\\
X_{c1}\in \mathbb{R}^p,X_{c2}\in \mathbb{R}^p\\
W=(w_{1},w_{2},\cdots ,w_{p})
\]
那么我们就可以分别得到它们的均值和方差:
\[\begin{aligned}
\bar{x}_{c1}&=\sum_{i=1}^{n1}w^Tx_{c1_{i}}\\
\bar{x}_{c2}&=\sum_{j=1}^{n2}w^Tx_{c2_{j}}\\
Var(x_{c1})&=\sum_{i=1}^{n1}(w^Tx_{c1_{i}}-\bar{x}_{c1})^2\\
Var(x_{c2})&=\sum_{j=1}^{n2}(w^Tx_{c2_{j}}-\bar{x}_{c2})^2
\end{aligned}
\]
根据类内小,类间大的思想,我们可以直接得到:
\[\hat{w}=\underset{w}{argmin}\frac{Var(x_{c1})+Var(x_{c2})}{(\bar{x}_{c1}-\bar{x}_{c2})^2}
\]
这个思想在支持向量机(Support Vector Machine,SVM)中也有体现。
逻辑回归
逻辑回归(Logistics Regression,LR)是一种判别式的线性分类方法,它通过对线性函数得到的值,通过激活函数\(sigmoid\)映射到\((0,1)\)来进行分类。
\[sigmoid(x)=\frac{1}{1+e^{-x}}
\]
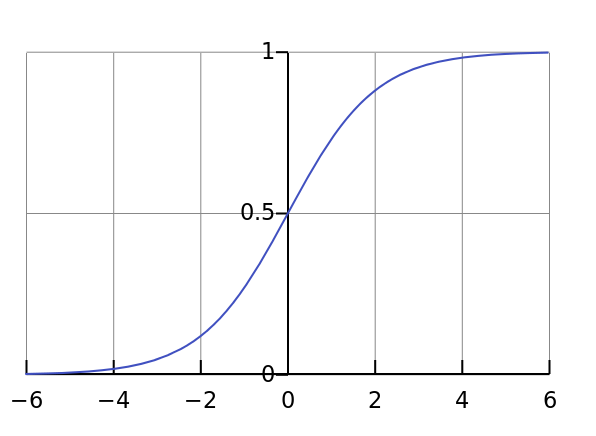
于是我们代入公式\((5)\)就可以得到:
\[\begin{aligned}
P(Y=1|X)&=sigmoid(W^TX)=\prod_{i=1}^{n}\frac{1}{1+exp(-w^Tx_{i})}\\
P(Y=0|X)&=1-P(Y=1|X)=\prod_{i=1}^{n}\frac{exp(-w^Tx_{i})}{1+exp(-w^Tx_{i})}
\end{aligned}
\]
代入极大似然估计得到:
\[\begin{aligned}
\hat{W}_{MLE}&=\underset{w}{argmax}P(Y|X)\\
&=\underset{w}{argmax}\sum_{i=1}^{n}(y_{i}log\;p(y_{i}=1|x_{i})+(1-y_{i})log\;p(y_{i}=0|x_{i}))\\
&=\underset{w}{argmax}\sum_{i=1}^{n}(y_{i}log\;\frac{1}{1+exp(-w^Tx_{i})})+(1-y_{i})log\;\frac{exp(-w^Tx_{i})}{1+exp(-w^Tx_{i})})\\
&=\underset{w}{argmax}\sum_{i=1}^{n}(-y_{i}log(1+exp(-w^Tx_{i}))-w^Tx_{i}-log(1+exp(-w^Tx_{i}))+y_{i}w^Tx_{i}+y_{i}log(1+exp(-w^Tx_{i})))\\
&=\underset{w}{argmax}\sum_{i=1}^{n}(y_{i}w^Tx-w^Tx_{i}-log(1+exp(-w^Tx_{i})))\\
&=\underset{w}{argmin}\sum_{i=1}^{n}-(y_{i}w^Tx-2w^Tx_{i}+log(1+exp(w^Tx_{i})))
\end{aligned}
\]
接下来求偏导:
\[\begin{aligned}
\frac{\partial \hat{W}_{MLE}}{\partial w}&=\sum_{i=1}^{n}-(y_{i}x_{i}-2x_{i}+\frac{exp(w^Tx_{i})}{1+exp(w^Tx_{i})})
\end{aligned}
\]
高斯判别分析
高斯判别分析(GDA)是一种生成式模型,判别式模型我们是直接去求解概率\(P(Y|X)\),而生成式模型是通过贝叶斯定理,判断\(P(Y=1|X)\)和\(P(Y=0|X)\)的大小来分类,并不需要去具体求两个概率的值。
首先我们先假设我们的数据分布:
- 根据贝叶斯定理,因为\(P(X)\)与\(Y\)无关,所以:\(P(Y|X)\propto P(X|Y)P(Y)\)
- 假设\(y_{i}\)服从伯努利分布:\(y_{i}\sim Bernoulli(\phi)\Rightarrow P(y_{i})=\phi^{y_{i}}(1-\phi)^{1-y_{i}}\)
- 假设\(X|Y\)服从高斯分布:\(P(X|Y=1)\sim N(\mu_{1},\sigma^2),P(X|Y=0)\sim N(\mu_{2},\sigma^2)\)
所以我们有:
\[\begin{aligned}
L(\mu_{1},\mu_{2},\sigma,\phi)&=log\prod_{i=1}^{n}p(y_{i}|x_{i})\\
&=log\prod_{i=1}^{n}p(x_{i}|y_{i})\cdot p(y_{i})\\
&=\sum_{i=1}^{n}(log\;p(x_{i}|y_{i})+log\;p(y_{i}))\\
&=\sum_{i=1}^{n}[y_{i}log\;N(\mu_{1},\sigma^2)+(1-y_{i})log\;N(\mu_{2},\sigma^2)+log\;(\phi^{y_{i}}(1-\phi)^{1-y_{i}})]\\
\end{aligned}
\]
(1)我们先对\(\phi\)求偏导:
\[\begin{aligned}
\frac{\partial L(\mu_{1},\mu_{2},\sigma,\phi)}{\partial \phi}&=\frac{\partial }{\partial \phi}\sum_{i=1}^{n}log\;(\phi^{y_{i}}(1-\phi)^{1-y_{i}})\\
&=\frac{\partial }{\partial \phi}\sum_{i=1}^{n}[y_{i}log\phi+(1-y_{i})log(1-\phi)]\\
&=\sum_{i=1}^{n}[\frac{y_{i}}{\phi}-\frac{1-y_{i}}{1-\phi}]\\
&=\sum_{i=1}^{n}\frac{y_{i}-\phi}{\phi(1-\phi)}=0
\end{aligned}
\]
最后我们得到:
\[\sum_{i=1}^{n}y_{i}=n\phi\Rightarrow \hat{\phi}=\frac{count(Y=1)}{n}
\]
上面这个式子中,其实\(\sum_{i=1}^{n}y_{i}\)就是\(Y=1\)的样本有多少个。
(2)我们对\(\mu1,\mu2\)求偏导,这两个是对称的,所以求出一个,另一个也就有了,这里我就直接给结论了,把高斯分布代入计算:
\[\hat{\mu}_{1},\hat{\mu}_{2}=\frac{\sum_{i=1}^{n}y_{i}x_{i}}{count(Y=1)}
\]
(3)接下来对\(\sigma\)求偏导:
\[\hat{\sigma}=\frac{1}{n}[count(Y=1)\cdot \left \| x_{i}-\mu_{1} \right \|^2+count(Y=0)\cdot \left \| x_{i}-\mu_{2} \right \|^2]
\]






