「Note」数据结构方向 - 可持久化数据结构

1. 可持久化线段树

1.1. 简介

可持久化线段树一般用于解决区间第 $k$ 小值的询问。
首先考虑简化过的问题，区间 $[1,r]$ 的第 $k$ 小值。

考虑用权值线段树（离散化或动态开点）来求 $k$ 小值，接下来只需要解决区间的问题。
可持久化线段树核心思想：每次插入值时保留历史版本，来实现区间查询第 $k$ 小。若每次修改暴力地复制一颗线段树显著不可行，考虑到每次修改最多影响 $\log n$ 级别个数的节点，我们将这些受影响的节点分离出来进行建树，如下图（源于 OI-wiki）。

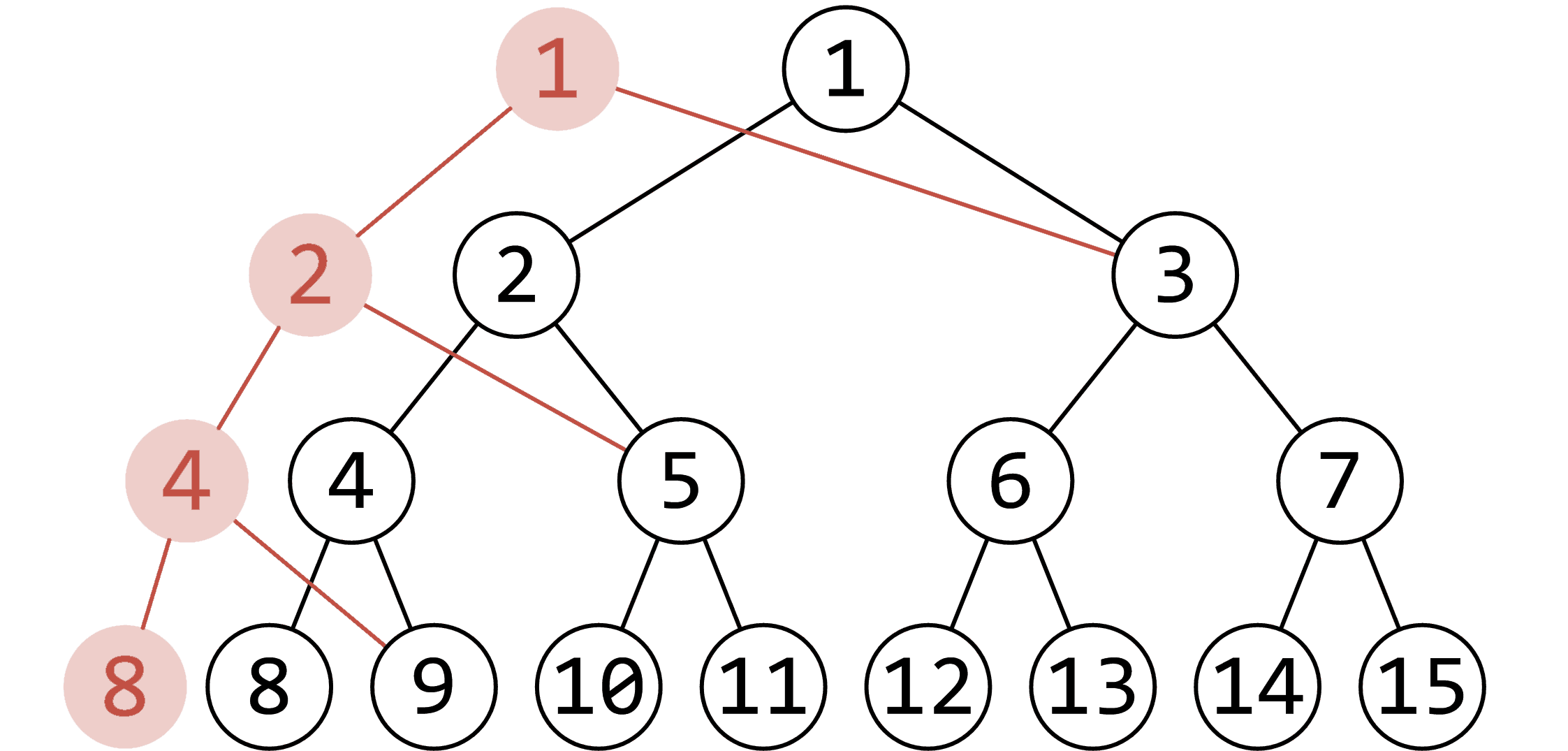
我们按顺序一个一个插入值，对于区间 $[1,r]$ 的第 $k$ 小值，只需要访问插入第 $r$ 个值后的那个版本即可。
至于区间 $[l,r]$ 的第 $k$ 小值，只需要使用区间 $[1,r]$ 的信息减去区间 $[1,l-1]$ 的信息便可求出。

1.2. 例题

$P3834$

板子。

$\text{Code}$：

``` #include #define LL long long #define UN unsigned using namespace std; //--------------------// //IO inline int rd() { int ret=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();} while(ch>='0'&&ch<='9')ret=ret*10+ch-'0',ch=getchar(); return ret*f; } //--------------------// const int N=2e5+5;

int n,m;
int s[N];
int tcnt,tem[N],id[N];
//--------------------//
const int TN=64e5+5;
struct Seg_Tree
{
struct Seg_Tree_Node
{
int ls,rs;
int val;
}t[TN];
int root[N],tot=0;
void build(int &rt,int L,int R)
{
rt=++tot;
if(LR)
return;
int mid=L+R>>1;
build(t[rt].ls,L,mid);
build(t[rt].rs,mid+1,R);
return;
}
void change(int &rt,int lst,int L,int R,int pos)
{
rt=++tot;
t[rt]=t[lst];
t[rt].val++;
int mid=L+R>>1;
if(LR)
return;
if(pos<=mid)
change(t[rt].ls,t[lst].ls,L,mid,pos);
else
change(t[rt].rs,t[lst].rs,mid+1,R,pos);
return;
}

int query(int rt,int pre,int L,int R,int rk)
{
	if(L==R)
		return L;
	int mid=L+R>>1;
	if(rk<=t[t[rt].ls].val-t[t[pre].ls].val)
		return query(t[rt].ls,t[pre].ls,L,mid,rk);
	return query(t[rt].rs,t[pre].rs,mid+1,R,rk-(t[t[rt].ls].val-t[t[pre].ls].val));
}

}T;
//--------------------//
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&s[i]),tem[++tcnt]=s[i];
sort(tem+1,tem+tcnt+1);
tcnt=unique(tem+1,tem+tcnt+1)-tem-1;
T.build(T.root[0],1,tcnt);
for(int temp,i=1;i<=n;i++)
{
temp=lower_bound(tem+1,tem+tcnt+1,s[i])-tem;
id[temp]=s[i];
s[i]=temp;
T.change(T.root[i],T.root[i-1],1,tcnt,s[i]);
}
for(int l,r,rk,i=1;i<=m;i++)
{
scanf("%d%d%d",&l,&r,&rk);
printf("%d\n",id[T.query(T.root[r],T.root[l-1],1,tcnt,rk)]);
}
return 0;
}

</details>