正态分布的模拟

　　题目来源于《R语言的科学编程与仿真》第18章第18题，原题如下：

参数为$\alpha$的柯西分布的概率密度函数为

\[f_{X}(x)=\frac{\alpha }{\pi \left ( \alpha ^{2}+x^2 \right )},-\infty<x<+\infty\]

使用逆变换法编写一个程序模拟柯西分布。现在考虑根据广义拒绝法使用一个柯西包络生成服从标准正态分布的随机变量。

　　先介绍一下逆变换法。假设给定$U\sim U(0,1)$，并且我们准备模拟具有累积分布函数为$F_{X}$的连续型随机变量$X$。令$Y=F_{X}^{-1}(U)$，那么我们有

\[F_{Y}(y)=P(Y\leqslant y)=P(F_{X}^{-1}(U)\leqslant y)=P(U\leqslant F_{X}(y))=F_{X}(y)\]

也即是，$Y$与$X$具有相同的分布。因此，如果我们能模拟服从$U(0,1)$分布的随机变量，那么我们就能模拟任意已知$F_{X}^{-1}$的随机变量$X$。

　　然后是广义拒绝法。为了模拟密度函数$f_{X}$，我们假设有可以模拟的包络密度$h$以及$k<\infty$使得$sup_{x}\frac{f_{X}(x)}{h(x)}\leqslant k$。具体步骤如下：

1.由$h$模拟$X$。

2.生成$Y\sim U(0,kh(X))$。

3.如果$Y<f_{X}(x)$那么返回$X$，否则返回步骤1。

　　为了提高广义拒绝法的效率，我们需要选择的$k$是越小越好。此题中，$h(x)=\frac{\alpha }{\pi \left ( \alpha ^{2}+x^2 \right )},f_{X}(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$。经过计算，当$k=\sqrt{2\pi}\frac{1}{\alpha}e^{\frac{\alpha^2}{2}-1},\alpha=1$时，k取得最小值。此时柯西分布的$\alpha$参数取值为1，刚好是标准柯西分布。

　　结合上述分析，具体代码实现如下：

cauchy<-function(x,alpha){
  alpha/(pi*(alpha^2+x^2))
} # 柯西分布的概率密度函数

cauchy_sim<-function(alpha){
  if(alpha<=0){
    stop('alpha should be greater than zero')
  }
  U<-runif(1)
  return(alpha*tanpi(U-1/2))
} # 逆变换法模拟柯西分布

k<-function(alpha){sqrt(2*pi)/alpha*exp(alpha^2/2-1)} # k是alpha的函数

norm_sim<-function(h,hsim,k,...){ # 用 ... 将参数alpha传给h()和hsim()函数 
  while(TRUE){
  x<-hsim(...)
  x1<-h(x=x,...)
  y<-runif(n=1,min=0,max=k(...)*h(x,...))
  if(y<dnorm(x,mean=0,sd=1)){
    return(x) # 利用return()终止循环
  }
  }
} # 模拟标准正态分布取值的函数

norm_sim(h=cauchy,hsim=cauchy_sim,k=k,alpha=1)

 

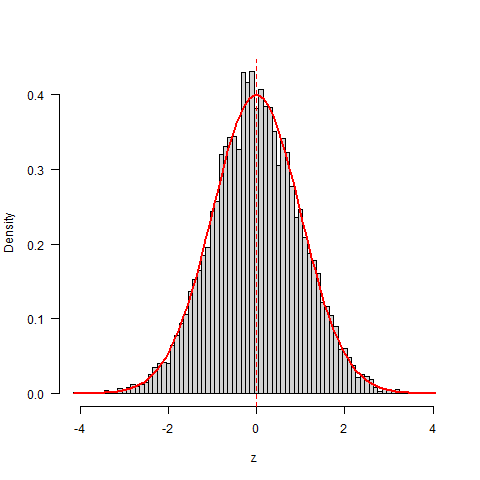
 　　下面画图比较模拟分布和真实分布的之间差异。

z<-replicate(1e4,
     norm_sim(h=cauchy,hsim=cauchy_sim,
                  k=sqrt(2*pi)/exp(0.5),alpha=1)) # 模拟一万个观测，用频率估计概率
breaks<-seq(range(z)[1]-0.1,range(z)[2]+0.1,0.1)
par(las=1)
hist(z,breaks=breaks,freq=FALSE,main='') # 模拟分布直方图
lines(breaks,dnorm(breaks,mean=0,sd=1),col='red',lwd=2) # 真实分布概率密度曲线
abline(v=0,col='red',lty=2)               

 　　图形如下：