二分搜索树
目录
1.二分查找
二分搜索树解决的是查找问题。
1.1递归,非递归实现
//非递归
template<typename T>
int binarySearch(T array[], int n, T target)
{
//在array[l...r]中查找
int l = 0;
int r = n - 1;
while ( l <= r )
{
int mid = l + (r - l) / 2;
if (array[mid] == target)
return mid;
if (array[mid] < target)
l = mid + 1;
else
r = mid - 1;
}
return -1;
}
//递归
template<typename T>
int binarySearch(T array[], int n, T target)
{
int l = 0;
int r = n - 1;
return __binarySearch(array, l, r, target);
}
template<typename T>
int __binarySearch(T array[], int l, int r, T target)
{
int mid = l + (r - l) / 2;
if (array[mid] == target)
return mid;
if (array[mid] < target)
__binarySearch(array, l, mid - 1, target);
else
__binarySearch(array, mid + 1, r, target);
}
1.2利用二分查找实现 floor(),ceil()函数
// 地板函数
// 如果找到target, 返回第一个target相应的索引index
// 如果没有找到target, 返回比target小的最大值相应的索引, 如果这个最大值有多个, 返回最大索引
// 如果这个target比整个数组的最小元素值还要小, 则不存在这个target的floor值, 返回-1
template<typename T>
int floor(T arr[], int n, T target){
assert( n >= 0 );
// 寻找比target小的最大索引
int l = -1, r = n-1;
while( l < r ){
// 使用向上取整避免死循环
int mid = l + (r-l+1)/2;
if( arr[mid] >= target )
r = mid - 1;
else
l = mid;
}
assert( l == r );
// 如果该索引+1就是target本身, 该索引+1即为返回值
if( l + 1 < n && arr[l+1] == target )
return l + 1;
// 否则, 该索引即为返回值
return l;
}
// 天花板函数
// 如果找到target, 返回最后一个target相应的索引index
// 如果没有找到target, 返回比target大的最小值相应的索引, 如果这个最小值有多个, 返回最小的索引
// 如果这个target比整个数组的最大元素值还要大, 则不存在这个target的ceil值, 返回整个数组元素个数n
template<typename T>
int ceil(T arr[], int n, T target){
assert( n >= 0 );
// 寻找比target大的最小索引值
int l = 0, r = n;
while( l < r ){
// 使用普通的向下取整即可避免死循环
int mid = l + (r-l)/2;
if( arr[mid] <= target )
l = mid + 1;
else // arr[mid] > target
r = mid;
}
assert( l == r );
// 如果该索引-1就是target本身, 该索引+1即为返回值
if( r - 1 >= 0 && arr[r-1] == target )
return r-1;
// 否则, 该索引即为返回值
return r;
}
1.3利用二分查找实现lower_bound(),upper_bound()函数
// 二分查找法, 实现lower_bound
// 即在一个有序数组arr中, 寻找大于等于target的元素的第一个索引
// 如果存在, 则返回相应的索引index
// 否则, 返回arr的元素个数 n
template<typename T>
int lower_bound(T arr[], int n, T target){
assert(n >= 0);
int l = 0, r = n;
while(l != r){
int mid = l + (r - l) / 2;
if(arr[mid] < target)
l = mid + 1;
else // nums[mid] >= target
r = mid;
}
return l;
}
// 二分查找法, 实现upper_bound
// 即在一个有序数组arr中, 寻找大于target的元素的第一个索引
// 如果存在, 则返回相应的索引index
// 否则, 返回arr的元素个数 n
template<typename T>
int upper_bound(T arr[], int n, T target){
assert(n >= 0);
int l = 0, r = n;
while(l != r){
int mid = l + (r - l) / 2;
if(arr[mid] <= target)
l = mid + 1;
else // nums[mid] > target
r = mid;
}
return l;
}
2.二分搜索树定义

3.二分搜索树操作
3.1插入
//insert 递归版
void *insert(Key key, Value value)
{
root = __insert(root, key, value);
}
//向以 node 为根节点的树中插入元素
Node *__insert(Node *node, Key key, Value value)
{
if (node == NULL)
{
count++;
return new Node(key, value);
}
if (node->key == key)
{
node->value = value;
}
if (node->key > key)
node->right = insert(node->right, key, value);
else
node->left = insert(node->left, key, value);
return node;
}
//insert 非递归版
void *insert(Key key, Value value)
{
Node *pre = root;
Node *p = root;
if (p == NULL)
{
count++;
root = new Node(key, value);
return;
}
while (p)
{
if (p->key == key)
{
p->value = value;
return;
}
if (p->key < key)
{
pre = p;
p = p->right;
}
else
{
pre = p;
p = pre->left;
}
}
if (pre->left == p)
pre->left = new Node(key, value);
else
pre->right = new Node(key, value);
}
3.2查找
Node *search(Key key)
{
return __search(root, key);
}
//查找以node为根节点的树中key所对应的value值
Value *__search(Node *node,Key key)
{
if (node == NULL)
{
return NULL;
}
if (node->key == key)
return &(node->value);
if (node->key < key)
return __contain(node->right, key);
else
return __contain(node->left, key);
}
3.3遍历(深度,层次)
//前序遍历
void preOrder()
{
__preOrder(root);
}
void __preOrder(Node *node)
{
if (node != NULL)
{
cout << node->value << endl;
__preOrder(node->left);
__preOrder(node->right);
}
}
//中序遍历
void inOreder()
{
__inOrder(root);
}
void __inOrder(Node *node)
{
if (node != NULL)
{
__inOrder(node->left);
cout << node->value << endl;
__inOrder(node->right);
}
}
//后序遍历
void postOreder()
{
__postOrder(root);
}
void __postOrder(Node *node)
{
if (node != NULL)
{
__postOrder(node->left);
__postOrder(node->right);
cout << node->value << endl;
}
}
//层次遍历
void levelOrder()
{
queue<Node*> q;
q.push(root);
while (!q.empty())
{
Node *node = q.front();
q.pop();
count--;
cout << node->key << endl;
if (node->left)
q.push(node->left);
if (node->right)
q.push(node->right);
}
}
3.4删除最小值
1.直接删除
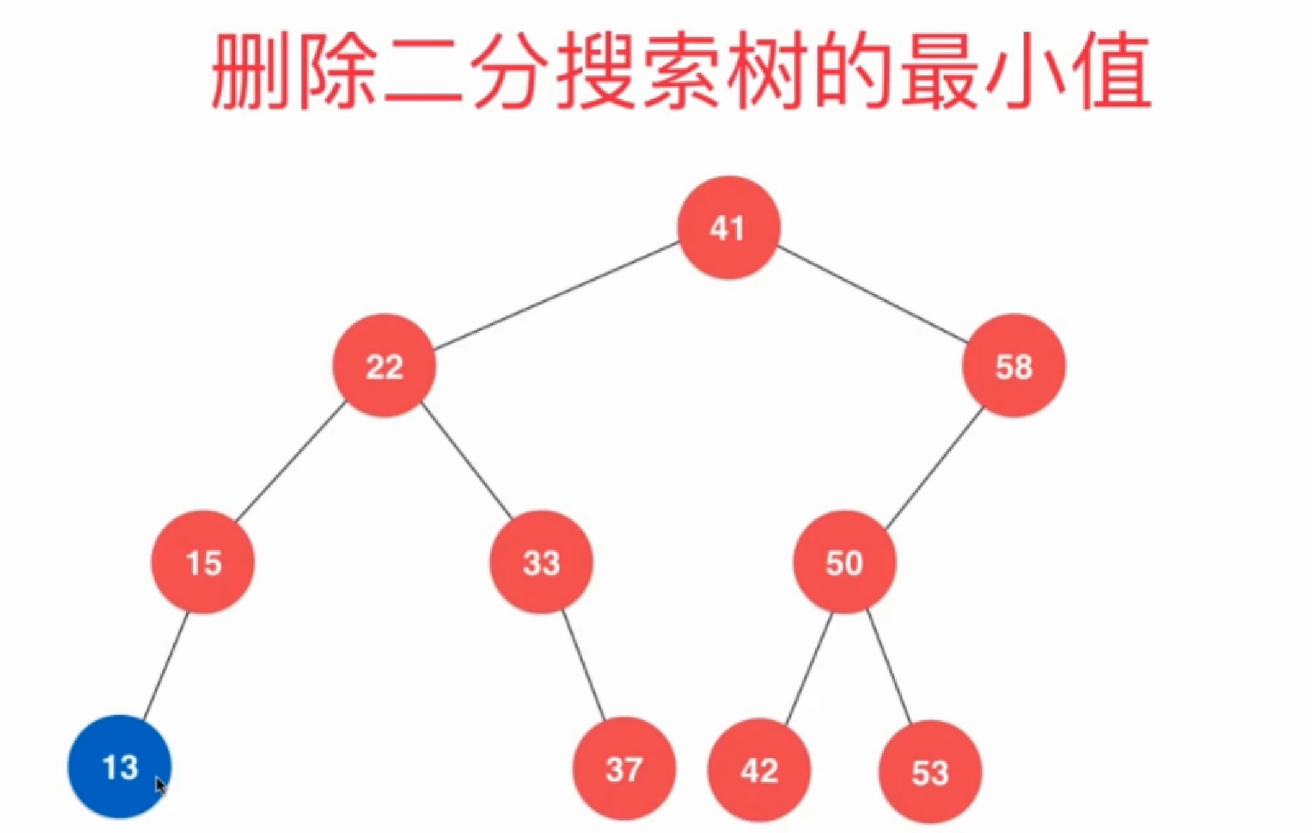
2.调整删除
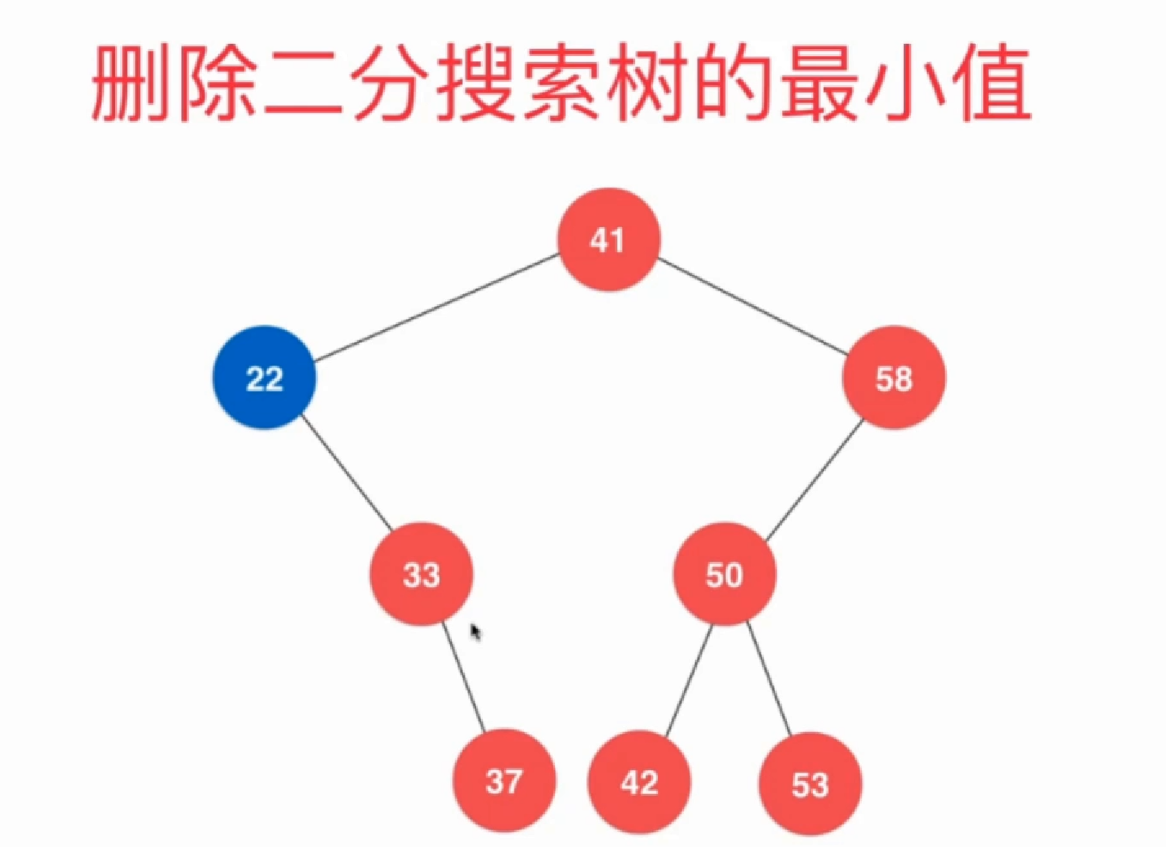
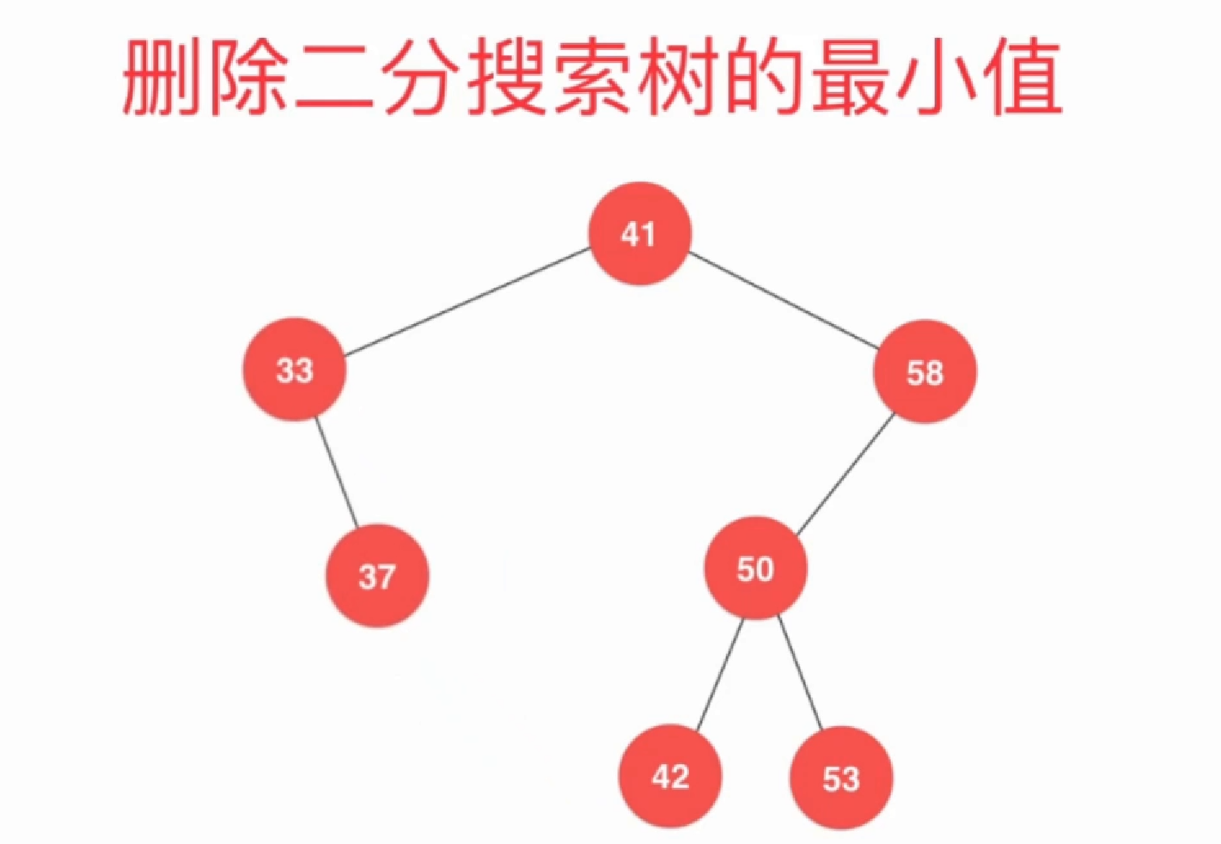
void removeMin()
{
if (root)
{
root = __removeMin(root);
}
}
//删除 以node为根的树的最小值
Node *__removeMin(Node *node)
{
if (node->left == NULL)
{
Node *rightNode = node->right; //当前要删节点的右孩子
delete node;
count--;
return rightNode;
}
node->left = __removeMin(node->left);
return node;
}
3.5删除最大值
- 直接删除
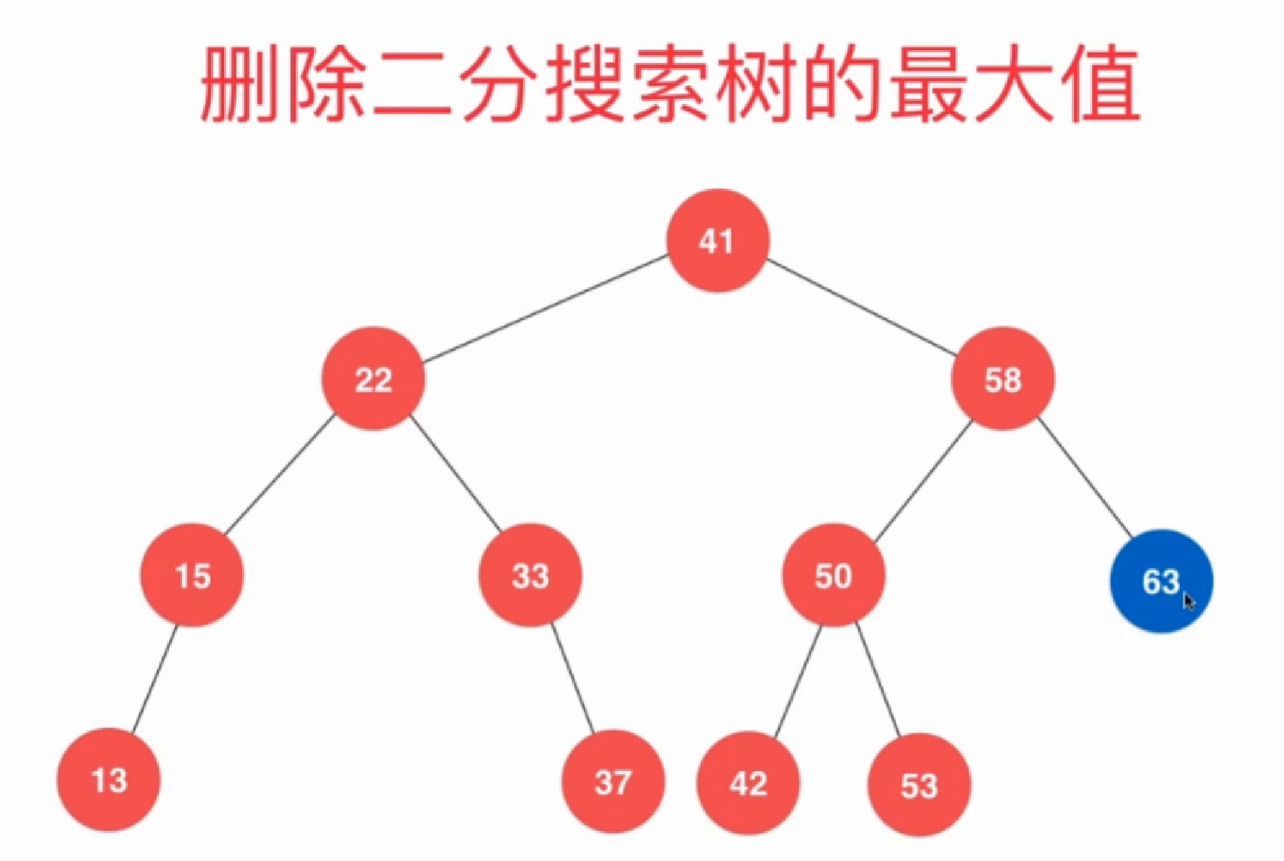
- 调整删除
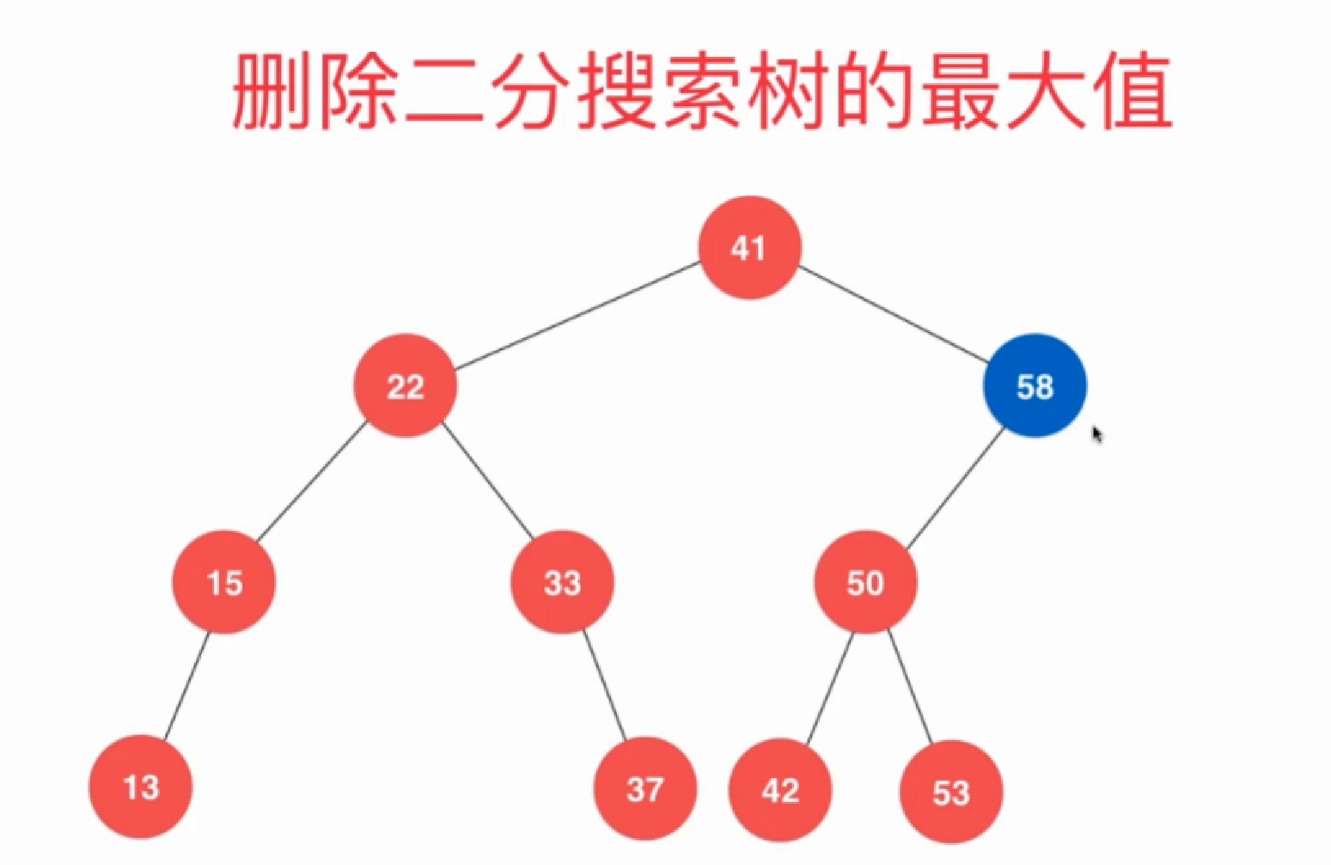
void removeMax()
{
if (root)
{
root = __removeMax(root);
}
}
//删除 以node为根的树的最大值
Node *__removeMax(Node *node)
{
if (node->right == NULL)
{
Node *leftNode = node->left; //当前要删节点的右孩子
delete node;
count--;
return leftNode;
}
node->right = __removeMin(node->right);
return node;
}
3.6删除任意节点
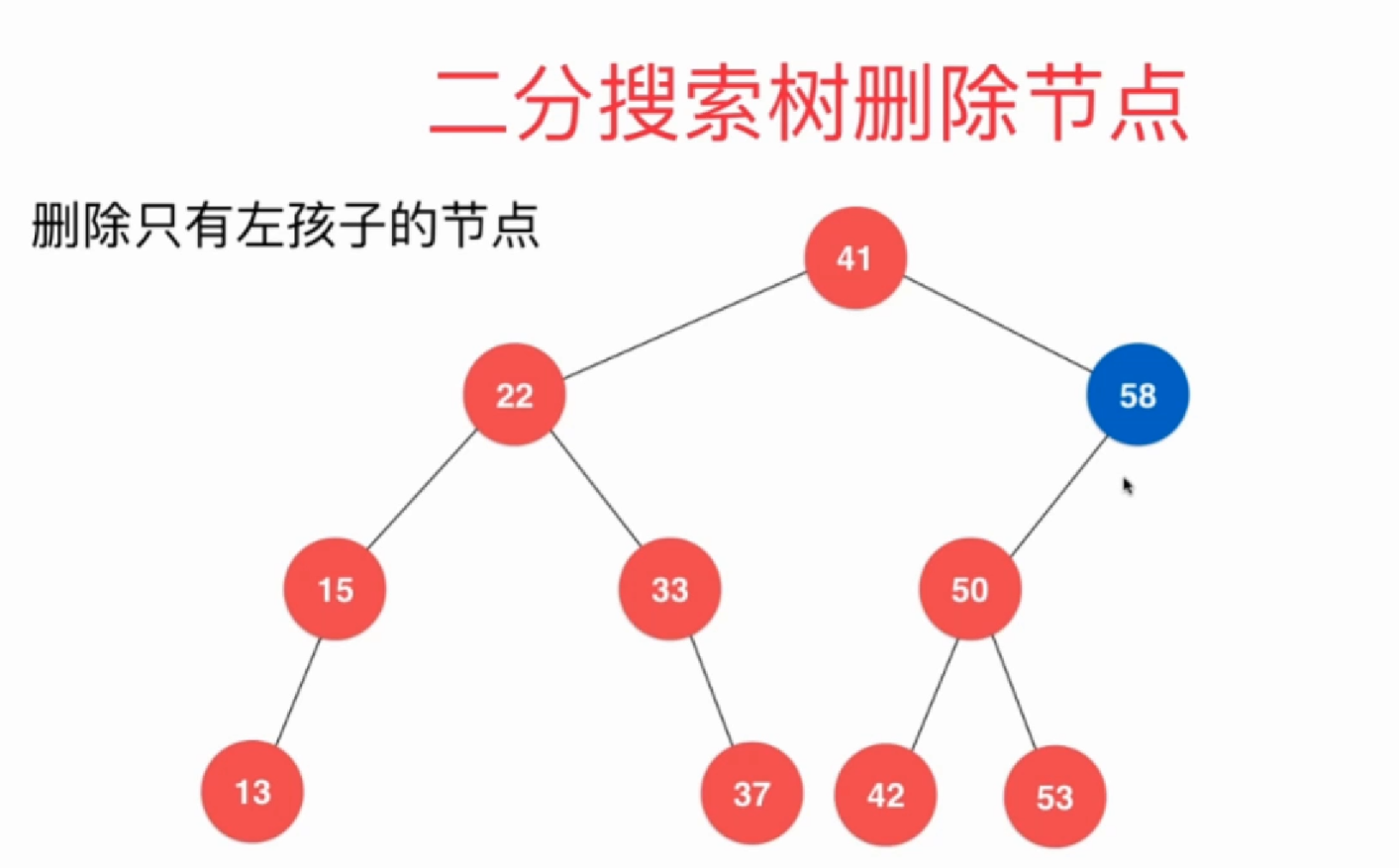
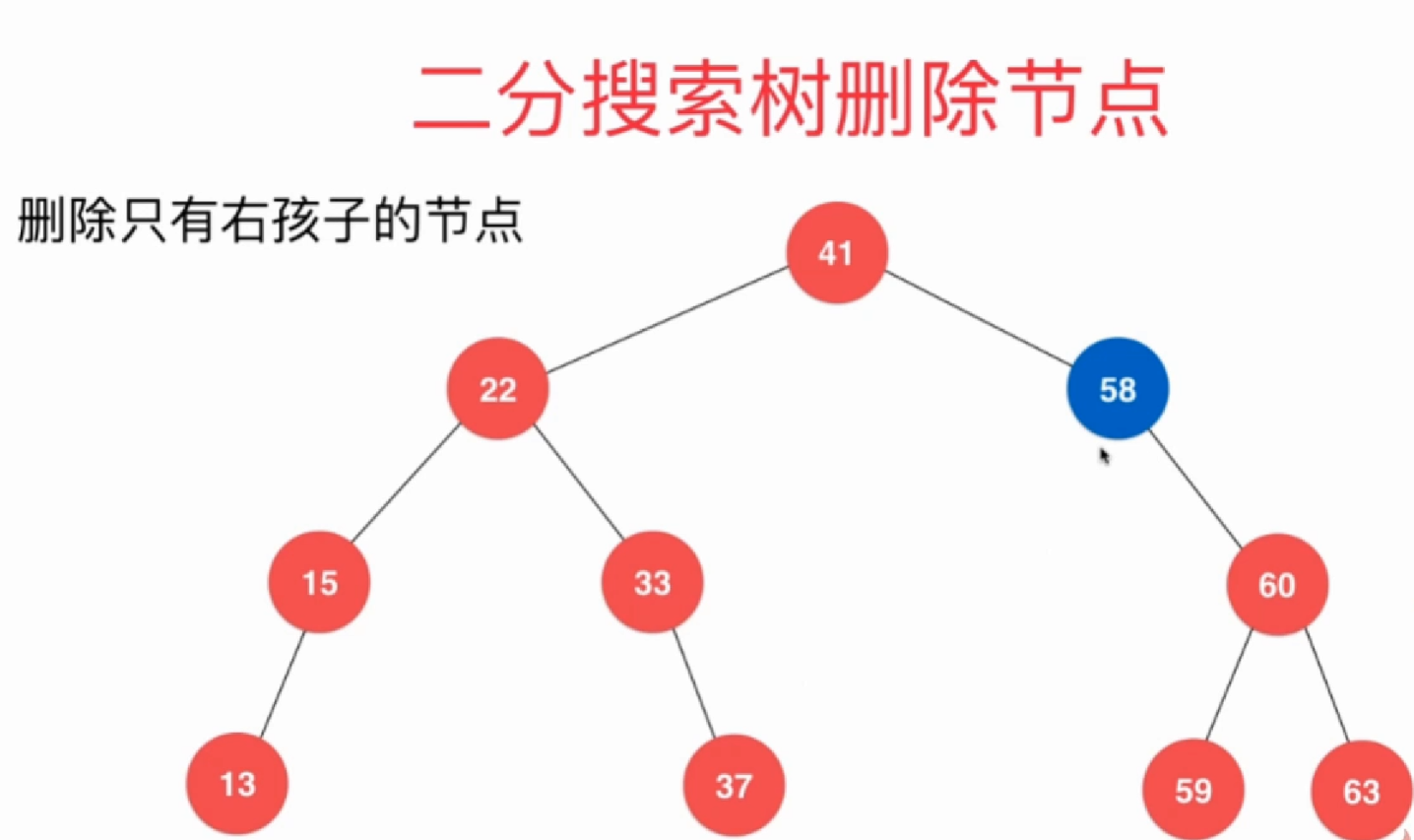

//删除 任意节点
void remove(Key key)
{
root = __remove(root, key);
}
Node *__remove(Node *node,Key key)
{
if (node == NULL)
{
return NULL;
}
if (node->key > key)
{
node->left = __remove(node->left, key);
return node;
}
else if (node->key < key)
{
node->right = __remove(node->right, key);
return node;
}
else
{
if (node->left == NULL) //与删除最小值类似
{
Node *rightNode = node->right;
delete node;
count--;
return rightNode;
}
else if (node->right == NULL) //与删除最大值类似
{
Node *leftNode = node->left;
delete node;
count--;
return leftNode;
}
else //node->left!=NULL && node->right!=NULL
{
//找到右子树中的最小值,即为即将代替要删节点
/*Node *successor = __minimum(node->right);
successor->right = __removeMin(node->right);*/
//上式__removeMin()会将successor删除,致使successor变为空指针
//解决:将右子树中的最小值复制一份,另写一个Node构造函数
Node *successor = new Node(__minimum(node->right));
count++;
successor->right = __removeMin(node->right);
successor->left = node->left;
delete node;
count--;
return successor;
}
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号