1.概念
在归并排序中,一个数组被**等分** 为两部分,而在快速排序中,切分位置取决于数组的内容。所以对于特殊形式的数据,可能会参数低劣的性能。。。
2.初实现
template<typename T>
void quickSort(T arr[], int n)
{
__quickSort(arr, 0, n - 1);
}
template<typename T>
void __quickSort(T arr[], int l, int r)
{
if(l>=r)
return;
int p = __partion(arr, l, r);
__quickSort(arr, l, p - 1);
__quickSort(arr, p + 1, r);
}
template <typename T>
int __partition(T arr[], int l, int r){
T v = arr[l];
int j = l; // arr[l+1...j] < v ; arr[j+1...i) > v
for( int i = l + 1 ; i <= r ; i ++ )
if( arr[i] < v ){
j ++;
swap( arr[j] , arr[i] );
}
swap( arr[l] , arr[j]);
return j;
}
3.当数组为近乎有序时
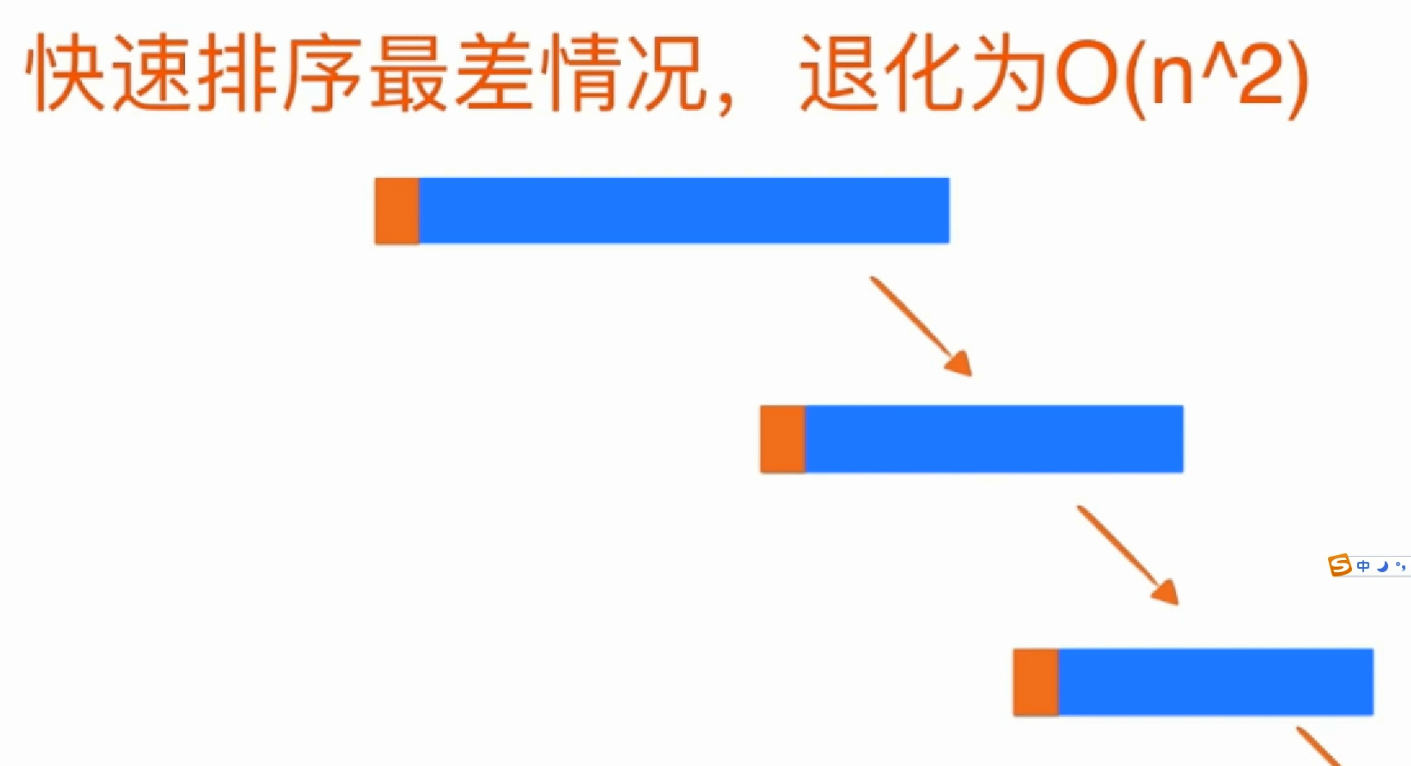
在第二节编写的代码,已经可以很好地处理大部分的场景问题了,但当数组为近乎有序时,在最差的情况下,快速排序将退化为O(n^2)。这是因为每次是把数组的最左边的元素作为分割点,数组右边的数都是比分割点大的,所以分割后会极度不平衡,如下图所示。
![]()
解决的方法其实很简单,只要每次随机的选取数组中的某个元素作为分割点就可以了。
template<typename T>
void quickSort(T arr[], int n)
{
srand(time(NULL));
__quickSort(arr, 0, n - 1);
}
template<typename T>
void __quickSort(T arr[], int l, int r)
{
// 优化1:对于小规模数组, 使用插入排序进行优化
if (r - l <= 15) {
insertionSort(arr, l, r);
return;
}
int p = __partion(arr, l, r);
__quickSort(arr, l, p - 1);
__quickSort(arr, p + 1, r);
}
template<typename T>
int __partion(T arr[], int l, int r)
{
//优化2:随机选择目标数
swap(arr[l], arr[rand() % (r - l + 1) + l]);
T tmp = arr[l];
int i = l;
for (int k=l+1; k<=r; k++)
{
if (arr[k] <= tmp)
{
swap(arr[i + 1], arr[k]);
i++;
}
}
swap(arr[l], arr[i]);
return i;
}
4.当数组中存在大量重复元素时
4.1方法一:双路快排
从左边开始遍历,直到找到一个元素比标定点大;从右边开始遍历,直到找到一个元素比标定点小,然后将两元素互换,那么小的元素就变为标定点元素的左边,而大的元素就放在了标定点元素的右端。
// 双路快速排序的partition
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
template <typename T>
int _partition2(T arr[], int l, int r){
// 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
swap( arr[l] , arr[rand()%(r-l+1)+l] );
T v = arr[l];
// arr[l+1...i) <= v; arr(j...r] >= v
int i = l+1, j = r;
while( true ){
// 注意这里的边界, arr[i] < v, 不能是arr[i] <= v
// 例如:数组1,0,0,....0, 若是arr[i] <= v,那么将一直循环,直到i=r,导致两棵子树不平衡
while( i <= r && arr[i] < v )
i ++;
// 注意这里的边界, arr[j] > v, 不能是arr[j] >= v
while( j >= l+1 && arr[j] > v )
j --;
if( i > j )
break;
swap( arr[i] , arr[j] );
i ++;
j --;
}
swap( arr[l] , arr[j]);
return j;
}
4.2方法二:三路快排(< == >)
将数组分为三类,左边区域比标定点值小,中间区域和标定点值相等,右边区域比标定点值大。
template <typename T>
void quickSort3Ways(T arr[], int n){
srand(time(NULL));
__quickSort3Ways( arr, 0, n-1);
}
template <typename T>
void __quickSort3Ways(T arr[], int l, int r){
// 对于小规模数组, 使用插入排序进行优化
if( r - l <= 15 ){
insertionSort(arr,l,r);
return;
}
// 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
swap( arr[l], arr[rand()%(r-l+1)+l ] );
T v = arr[l];
int lt = l; // arr[l+1...lt] < v 初始为空!
int gt = r + 1; // arr[gt...r] > v 初始为空!
int i = l+1; // arr[lt+1...gt) == v
while( i < gt ){
if( arr[i] < v ){
swap( arr[i], arr[lt+1]);
i ++;
lt ++;
}
else if( arr[i] > v ){
swap( arr[i], arr[gt-1]);
gt --;
}
else{ // arr[i] == v
i ++;
}
}
swap( arr[l] , arr[lt] );
__quickSort3Ways(arr, l, lt-1);
__quickSort3Ways(arr, gt, r);
}
5.应用:寻找arr数组中第k小的元素
// partition 过程, 和快排的partition一样
template <typename T>
int __partition( T arr[], int l, int r ){
int p = rand()%(r-l+1) + l;
swap( arr[l] , arr[p] );
int j = l; //[l+1...j] < p ; [lt+1..i) > p
for( int i = l + 1 ; i <= r ; i ++ )
if( arr[i] < arr[l] )
swap(arr[i], arr[++j]);
swap(arr[l], arr[j]);
return j;
}
// 求出arr[l...r]范围里第k小的数
template <typename T>
int __selection( T arr[], int l, int r, int k ){
if( l == r )
return arr[l];
// partition之后, arr[p]的正确位置就在索引p上
int p = __partition( arr, l, r );
if( k == p ) // 如果 k == p, 直接返回arr[p]
return arr[p];
else if( k < p ) // 如果 k < p, 只需要在arr[l...p-1]中找第k小元素即可
return __selection( arr, l, p-1, k);
else // 如果 k > p, 则需要在arr[p+1...r]中找第k-p-1小元素
// 注意: 由于我们传入__selection的依然是arr, 而不是arr[p+1...r],
// 所以传入的最后一个参数依然是k, 而不是k-p-1
return __selection( arr, p+1, r, k );
}
// 寻找arr数组中第k小的元素
// 注意: 在我们的算法中, k是从0开始索引的, 即最小的元素是第0小元素, 以此类推
// 如果希望我们的算法中k的语意是从1开始的, 只需要在整个逻辑开始进行k--即可, 可以参考selection2
template <typename T>
int selection(T arr[], int n, int k) {
assert( k >= 0 && k < n );
srand(time(NULL));
return __selection(arr, 0, n - 1, k);
}
// 寻找arr数组中第k小的元素, k从1开始索引, 即最小元素是第1小元素, 以此类推
template <typename T>
int selection2(T arr[], int n, int k) {
return selection(arr, n, k - 1);
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号