学术--读书笔记：《复杂（新版）》--智能涌现的机理：自指？

作者：梅拉妮·米歇尔

 

简介：复杂来自与自指特性 self-reference，与集异壁有相似结论。（此书作者是集异壁作者侯世达学生。强人工智能应该与复杂性来源有相关性。简单的确定性方程（如逻辑斯蒂映射，包含自指）能产生类似于随机噪声的确定性轨道。遗传物质含有绝妙的自指特性：所有这些决定DNA的转录、翻译和复制的复杂细胞机制——m RNA、t RNA、核糖体、聚合酶，等等——本身都编码在DNA中。就像侯世达说的：“DNA中包含其本身的解码者的编码！”它也包含合成核苷酸的所有蛋白质的编码，而核苷酸是构造DNA的材料。如果图灵还活着，看到这种自指特性肯定会非常高兴。

人们在各种层面上都能很好地认识到两种事物和情形之间的类似之处，让各种概念从一种情形流畅地“滑到”另一种。现代计算机则对上下文一点也不敏感。（人类抽象能力 vs 机器特征提取。类比的能力需要什么组成，认知科学的范畴？）

 

第一部分 背景和历史

 

• 还原论最早的倡议者之一笛卡儿这样描述他的科学方法：“将面临的所有问题尽可能地细分, 细至能用最佳的方式将其解决为止”
• 复杂系统科学最关注的问题就是人体、经济、社会这种逆熵的自组织系统是如何实现

 

第1章 复杂性是什么

•    复杂系统试图解释，在不存在中央控制的情况下，大量简单个体如何自行组织成能够产生模式、处理信息甚至能够进化和学习的
•    如何度量复杂性

 

第2章 动力学、混沌和预测

 

简单的确定性方程（如逻辑斯蒂映射）能产生类似于随机噪声的确定性轨道，这个事实让人困扰。

• 混沌的性质 

第一条普适性质：通往混沌的倍周期。这些突然的周期倍增被称为分叉（bifurcation）。不断分叉直至混沌的过程就是“通往混沌的倍周期。倍周期之路并不是只有逻辑斯蒂映射才有，事实上任何抛物线形状的映射都有类似现象。这里“抛物线形状”意指映射的图形有一个隆起——用数学术语说就是“单峰。

 

第二条普适性质：费根鲍姆常数。
费根鲍姆注意到，随着周期增大，R值之间的距离越来越近。这意味着随着R的增大，分叉之间的间隔越来越短。在图2.15的分叉图中可以看到这一点。费根鲍姆用这些R值计算了分叉靠近的速度，也就是R值的收敛速度。他发现速度约等于常数4.6692016。这意味着随着R值增加，新的周期倍增比前面的周期倍增出现的速度快大约4.6692016
发现这个结果后，费根鲍姆接着又从理论上解释了为何常数4.6692016具有普适性——对所有单峰映射都成立。这个数现在被称为费根鲍姆常数。常数的理论解释使用了一种复杂的数学技巧——重正化（renormalization）。重正化最初是从量子力学中发展出来，后来又被应用到另一个物理学领域：相变和其他“临界现象”的研究。费根鲍姆将其引入了动力系统理论并成为理解混沌的重要手段。

• 混沌的共性
  
  • 混沌的发现给了精确预测的梦想最后一击。混沌指的是一些系统——混沌系统——对于其初始位置和动量的测量如果有极其微小的不精确，也会导致对其的长期预测产生巨大的误差。也就是常说的“对初始条件的敏感
  • 某些因素的物理尺度太小，以致无法被有局限性的人类注意，却有可能导致极为重要的误差。不是不能计算，而是人类局限，没有观测或发现规律
  • 如果我们能知道自然界的定律和宇宙在初始时刻的精确位置，我们就能精确预测宇宙在此后的情况。但是即便我们弄清了自然界的定律，我们也还是只能近似地知道初始状态。如果我们能同样近似地预测以后的状态，这也够了，我们也就能说现象是可以预测的，而且受到定律的约束。但并不总是这样，初始条件的细微差别有可能会导致最终现象的极大不同。前者的微小误差会导致后者的巨大误差。预测变得不可能
• 混沌思想带来的革命
  • 混沌系统中初始的不确定性到底是如何被急剧放大的呢？关键因素是非线性。对于线性系统，你可以先了解其组成，然后将它们合并。对于非线性系统，整体则不等于部分

第3章 信息

• 信息是什么

信息和计算这两个术语的意义有精确的定义。两者都是到20世纪才在数学上被定义。让人吃惊的是，两者居然都是从19世纪末的一个物理难题发展而来，这个难题中有个非常聪明的“小妖”，它似乎不用耗费任何能量就能做很多事情。这个难题曾让物理学家们非常担心，以为他们的基本定律可能哪里错了。

• 麦克斯韦妖

1871年，麦克斯韦在《论热能》（ Theory of Heat）一书中提出了一个难题，题为“热力学第二定律的局限”。麦克斯韦假设有一个箱子被一块板子隔成两部分，板子上有一个活门，如下图所示。活门有一个“小妖”把守，小妖能测量气体分子的速度。对于右边来的分子，如果速度快，他就打开门让其通过，速度慢就关上门不让通过。对于左边来的分子，则速度慢的就让其通过，速度快的就不让通过。一段时间以后，箱子左边分子速度就会很快，右边则会很慢，这样熵就增加。

 

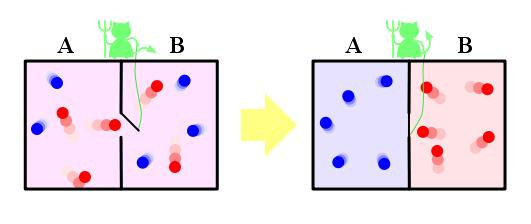
杰出的匈牙利物理学家西拉德（Leo Szilard）提出，做功的是小妖的“智能”，更精确地说，是通过测量获取信息的行为。 西拉德是第一个将熵与信息联系起来的人，这个关联后来成了信息论的基础和复杂系统的关键。

拉德认为测量过程（小妖要通过测量获取“比特”信息，比如趋近的分子速度是慢是快）需要能量，因此必然会产生一定的熵，数量不少于分子变得有序而减少的熵。这样由箱子、分子和小妖组成的整个系统就仍然遵守热力学第二定律

对小妖来说，也就是弄清分子是快是慢——而不用增加熵。班尼特的证明成了可逆计算（reversible computing）的基础，他证明在理论上可以进行任何计算而不用耗费能量。班尼特的发现似乎意味着小妖又回来了，因为测量可以不用耗费能量。不过，班尼特认为，物理学家兰道（Rolf Landauer）在20世纪60年代做出的一项发现可以挽救热力学第二定律：并不是测量行为，而是擦除记忆的行为，必然会增加熵。擦除记忆是不可逆的；如果被擦除了，那么一旦信息没有了，不进行额外的测量就无法恢复。班尼特证明，小妖如果要工作，到一定的时候就必须擦除记忆，如果这样，擦除的动作就会产生热，增加的熵刚好抵消小妖对分子进行分选而减少的能量

 

• 统计力学提要
  • 玻尔兹曼（Ludwig Boltzmann），他创建了一门新学科，现在被称为统计力学。
• 热力学第二定律被认为是定义了“时间之箭”，因为它证明了存在时间上不可逆的过程（比如，热量自发地回到你的冰箱，并转化成电能进行制冷）。“未来”可以定义为熵增的时间，第二定律是唯一区分过去和未来的基本物理定律。其他物理定律在时间上都是可逆的。为什么第二定律能区分过去和现在，而其他自然定律却不能？这也许是物理学中最大的难题。
• 香农信息
  • 人们有时候将香农的信息量定义描述为接收者在接收时体验到的“平均惊奇度”，其中“惊奇”意指接收者对于发送源将要传送的信息的“不确定。

 

第4章 计算

• 什么是计算？什么可以计算
• 希尔伯特问题和哥德尔定理图灵机和不可计算性
  • 德国数学大师希尔伯特（David Hilbert）于1900年在巴黎的国际数学家大会上提出来的。 希尔伯特在演讲中提出了世纪之交面临的23个亟待解决的数学问题，这些问题可以分为三个部分： 1.数学是不是完备的？也就是说，是不是所有数学命题都可以用一组有限的公理证明。2.数学是不是一致的？换句话说，是不是可以证明的都是真命题？“真命题”是专业术语，但我在这里用的是直接意义。假如我们证出了假命题，例如1+1=3，数学就是不一致的，这样就会有大麻烦。 3.是不是所有命题都是数学可判定的？也就是说，是不是对所有命题都有明确程序（definite procedure）可以在有限时间内告诉我们命题是真是假？这样你就可以提出一个数学命题，比如“所有比2大的偶数都可以表示为两个素数之和”，然后将它交给计算机，计算机就会用“明确程序”在有限时间内得出命题是“真”还是“假”的
    
    
• 定义为图灵机的明确程序
• 通用图灵机
• 图灵对判定问题的解决
• 哥德尔和图灵的命运

 

第5章 进化

• 达尔文之前的进化观念
• 达尔文理论的起源
• 孟德尔和遗传律
• 现代综合
• 对现代综合的挑战

 

第6章 遗传学概要

• 这其中含有绝妙的自指特性：所有这些决定DNA的转录、翻译和复制的复杂细胞机制——m RNA、t RNA、核糖体、聚合酶，等等——本身都编码在DNA中。就像侯世达说的：“DNA中包含其本身的解码者的编码！”它也包含合成核苷酸的所有蛋白质的编码，而核苷酸是构造DNA的材料。如果图灵还活着，看到这种自指特性肯定会非常高兴。

第7章 度量复杂性

 

2001年，物理学家劳埃德（Seth Lloyd）发表了一篇文章，提出了度量一个事物或过程的复杂性的三个维度： 描述它有多困难？ 产生它有多困难？ 其组织程度如何？ 劳埃德列出了40种度量复杂性的方法，这些方法分别是从动力学、热力学、信息论和计算等方面来考虑这三个问题。

• 用大小度量复杂性
• 用熵度量复杂性
• 用算法信息量度量复杂性
  • 事物的复杂性定义为能够产生对事物完整描述的最短计算机程序的长度。这被称为事物的算法信息量。
  • 物理学家盖尔曼（Murray Gell-Mann）提出了一种称为“有效复杂性（effective complexity）”的相关度量，[89] 更符合我们对复杂性的直观认识。盖尔曼认为任何事物都是规则性和随机性的。为了计算有效复杂性，首先要给出事物规则性的最佳描述；有效复杂性定义为包含在描述中的信息量或规则集合的算法信息量
    一个事物的逻辑深度是对构造这个事物的困难程度的度量。高度有序的A、C、G、T序列（例如前面的序列1）显然很容易构造。同样，如果我要你给我一个A、C、G、T的随机序列，你也很容易就可以做出来，用个硬币或骰子就可以了。但如果我要你给我一个能够生成可发育的生物的DNA序列，如果不偷看真正的基因组序列，任何一个生物学家都会觉得很难。 
  •  西蒙认为，复杂系统最重要的共性就是层次性和不可分解性。西蒙列举了一系列层次结构的复杂系统——例如，身体由器官组成，器官又是由细胞组成，细胞中又含有细胞子系统，等等。某种程度上，这个观念与分形在所有尺度上都自相似类似。 不可分解性指的是，在层次性复杂系统中，子系统内部的紧密相互作用比子系统之间要多得多。例如，细胞内部的新陈代谢网络就比细胞之间的作用要复杂得多。 西蒙还认为，进化之所以能设计出自然界中的复杂系统，正是因为它们能像砖块一样被结合到一起——也就是说，具有层次性和不可分解性。细胞能够进化，从而成为高一级器官的建筑模块，组成的器官又可作为更高一级器官的建筑模块。西蒙认为复杂系统研究需要有一个“层次。（笔者：参见《技术的本质》，中间需求的存在能大幅减少穷举数量）
  • 有逻辑深度的事物……从根本上必须是长时间计算或漫长动力过程的产物，否则就不可能。热力学深度首先是确定“产生出这个事物最科学合理的确定事件序列”，然后测量“物理构造过程所需的热力源和信息源的总量”。

 

第二部分 计算机中和生命和进化

 

• 冯·诺依曼结构的计算之所以容易描述，一个原因就是，编程语言层面和机器码层面可以毫无歧义地相互转化，因为计算机的设计让这种转化可以很容易做到。计算机科学提供了自动编译和反编译的工具，让我们可以理解具体的程序是如何处理信息的。 而元胞自动机则不存在这样的编译和反编译工具，至少目前还没有，也没有实用和通用的设计“程序”的高级语言。用粒子来帮助理解元胞自动机高级信息处理结构的思想也是最近才出现，还远没有形成此类系统的计算。
• 一个淋巴细胞表面覆盖的受体是一样的，可以与特定的某一类分子形状匹配。如果恰好遇到了形状相匹配的病原体分子（称为“抗原”），淋巴细胞的受体就会与其相结合，淋巴细胞就“识别”出了抗原，这是消灭病原体的第一步。结合可强可弱，依赖于分子与受体的匹配。
• 对于任何进入体内的病原体，身体很快就产生出能与病原体的标记分子（也就是抗原）相结合的淋巴细胞，虽然结合可能不是很紧密。 一旦发生了结合事件，免疫系统就得搞清楚这是不是真正的威胁。病原体当然是有害的，一旦它们进入身体，就会开始大量复制。不过发动免疫系统攻击会导致发炎等对身体有害的症状，攻击太强烈甚至有可能致命。免疫系统作为一个整体必须确定威胁是否足够严重，值得承担让免疫反应伤害身体的风险。免疫系统只有在强结合事件足够多之后才会进入高速运转
• B细胞和T细胞这两种类型的淋巴细胞协同工作，判断攻击是否有必要。一旦B细胞表面强结合受体的数量超过了某个阈值，或者有类似受体的T细胞那里收到了“发动”信号，B细胞就会被激活，表明它现在感觉到了身体受到威胁。一旦激活，B细胞就会向血液中释放抗体分子。这些抗体与抗原结合，使它们失效，并对它们进行标记，好让其他免疫细胞摧毁它们。 激活的B细胞被输送到淋巴结，在那里迅速分裂，产生出大量后代，复制时由于变异，许多后代的受体形状都改变了。然后这些后代会与淋巴结俘获的抗原进行测试。不能结合的细胞很快就会死去。 存活下来的后代被释放到血液中（惊！免疫力是这样筛选出来的，为什么不能结合的就死去？），其中一些会遇到抗原并与其结合，有时候会比它们的母细胞结合得更紧密。这些激活的B细胞同样又被输送到淋巴结，在那里产生出自己的后代。这也就是为什么当你病了的时候淋巴结会肿大。
• 通过与抗原结合和接收T细胞的“发动”信号激活B细胞的示意图。信号刺激B细胞产生和释放抗体（y形）
• 与抗原匹配得越好的B细胞产生的后代也越多。简而言之，这就是一个自然选择过程，B细胞群体进化出能与目标抗原紧密结合的受体形状，从而使得通过选择“设计”出来攻击特定抗原的抗体武器库
• 免疫学家们还没有完全弄清这些问题，现在这些问题都还是活跃的研究领域。有人认为避免攻击自身的一个主要机制是所谓的负选择（negative selection）。当淋巴细胞产生出来时，它们不会被立即释放到血液中去，它们会在骨髓和胸腺中进行测试，与身体自身的分子进行接触。与“自身”分子紧密结合的淋巴细胞可能会被杀死或对基因进行“编辑”以改变受体。也就是说免疫系统只使用不会攻击自身的淋巴细胞。这个机制经常会失效，有时候会产生出糖尿病或类风湿性关节炎这类自身免疫性疾病。 另一个防止自身免疫攻击的主要机制可能是调节性T细胞（regulatory T cells）的作用。调节性T细胞是T细胞的一个特殊亚种。
• 人们在各种层面上都能很好地认识到两种事物和情形之间的类似之处，让各种概念从一种情形流畅地“滑到”另一种。现代计算机则对上下文一点也不敏感。（人类抽象能力 vs 机器特征提取）
  
  

 侯世达的“并行级差扫描”：许多可能性被并行地进行探索，用获得的最新信息不断对各种可能性的收益进行估计，并根据反馈分配资源。同蚁群和免疫系统一样，所有可能性都有可能被探索，但是在同一时刻只有部分被探索，并且分配的资源也不一样多。当人（或蚁群，或免疫系统）对所面临的情形只有很少的信息时，对各种可能性的探索开始时非常随机、高度并行（同时考虑许多可能性）和分散：没有理由要特别考虑某种可能性。随着获得的信息越来越多，探索逐渐变得集中（增加的资源集中于少数可能性）和确定：确实有收益的可能性会被开发。这种探索策略也是通过简单个体的大量互动涌现