机器学习(07)——岭回归算法实战
1. 回归算法概念
回归分析是一种预测性的建模技术,它研究的是因变量(目标)和自变量(预测器)之间的关系。这种技术通常用于预测分析、时间序列模型以及发现变量之间的因果关系。
回归算法通过对特征数据的计算,从数据中寻找规律,找出数据与规律之间的因果关系,并根据其关系预测后续发展变化的规律以及结果。
常用回归算法有:线性回归算法、逐步回归算法、岭回归算法、lasso回归算法、支持向量机回归等。
2. 岭回归算法
岭回归(英文名:ridge regression, Tikhonov regularization)是一种专用于共线性数据分析的有偏估计回归方法,实质上是一种改良的最小二乘估计法,通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法,对病态数据的拟合要强于最小二乘法。
通常岭回归方程的R平方值会稍低于普通回归分析,但回归系数的显著性往往明显高于普通回归,在存在共线性问题和病态数据偏多的研究中有较大的实用价值。
适用情况:
1.可以用来处理特征数多于样本数的情况
2.可适用于“病态矩阵”的分析(对于有些矩阵,矩阵中某个元素的一个很小的变动,会引起最后计算结果误差很大,这类矩阵称为“病态矩阵”)
3.可作为一种缩减算法,通过找出预测误差最小化的λ,筛选出不重要的特征或参数,从而帮助我们更好地理解数据,取得更好的预测效果
3. 使用岭回归算法预测防火墙日志中,每小时总体请求数的变化
1)项目说明
防火墙日志会记录所有的外网对内网或内网对外网的访问请求,根据不同日期、时间段以及使用情况,请求数与ip数都在不停的变化,通过机器算法的学习,掌握其变化的规律,预测出当天的变化规律。
2)数据信息
已通过前期的数据处理,已经完成了请求统计记录与效果展示。
日志请求统计汇总表--小时
| 表名 | 字段名称 | 字段类型 | 主键 | 是否允许空 | 默认值 | 字段说明 |
|---|---|---|---|---|---|---|
| request_report_for_hour | id | serial | PK | 0 | 主键Id | |
| request_report_for_hour | date | timestamp | IX | 日期 | ||
| request_report_for_hour | hour | integer | IX | 0 | 小时 | |
| request_report_for_hour | tag | text | IX | 分类标签:total=汇总统计;device=设备名称 | ||
| request_report_for_hour | devname | text | IX | 防火墙设备名称 | ||
| request_report_for_hour | request_for_total | integer | IX | 0 | 总请求数 | |
| request_report_for_hour | ip_for_total | integer | IX | 0 | 总IP数 |
日志请求统计汇总表数据
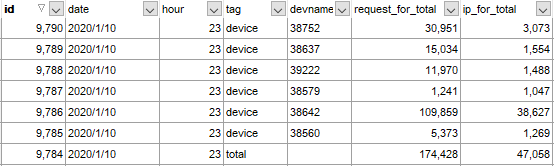
日志请求统计汇总表效果图
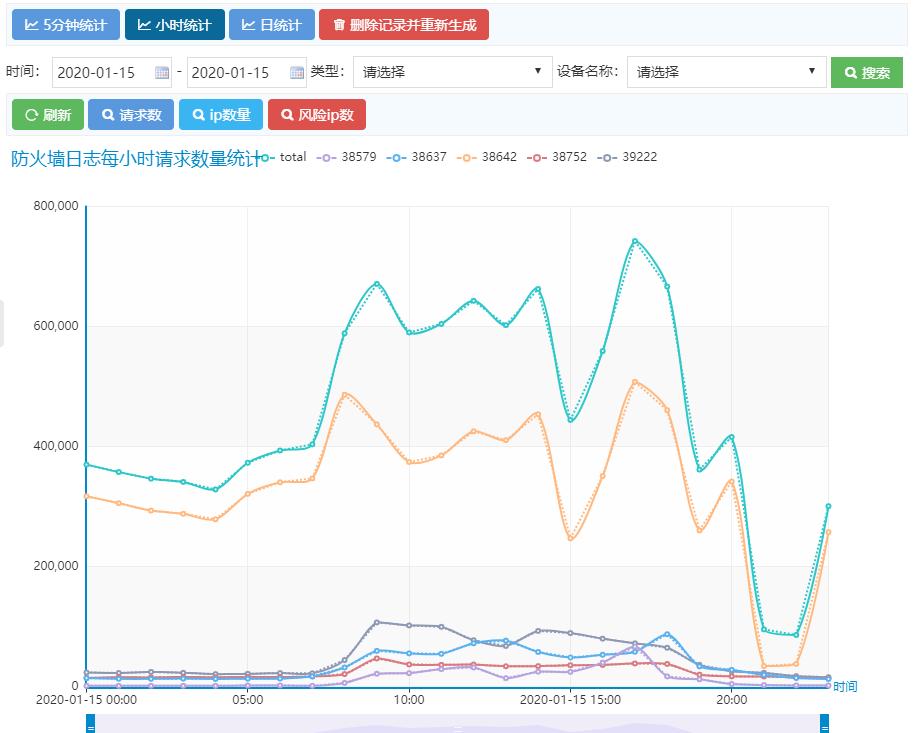
3)设计思路
根据这些已有数据,我们需要做的是,将数据和数据中所包含的特征,转换成机器学习可以计算的数值数据,然后使用回归算法对这些数据进行运算,找出这些数据的变化规律,然后根据这些规律,预测其未来的变化值。
业务问题思考
对于已记录的数据,我们需要思考的问题有:
- 对于这种数值结果的预测,可以使用回归算法来处理,而请求数变化这种类型,应该使用什么回归算法比较合适?
- 使用的回归算法,需要提供什么数据来进行学习和预测?
- 根据“日志请求统计汇总表”的字段设计,我们能用于分享的特征有日期、小时、汇总统计和防火墙设备名称。而可用于机器学习的标签(答案)有总请求数和总ip数,怎么将已有的这些内容转换成机器学习可以使用的数据?
- 这些已有数据是否够用?需要新增哪些字段来帮助机器学习,提升预测的准确率?
- 对于字符串类型的特征,要怎么转换?设计什么值比较合理?不同的设计方案会有什么样的区别?对预测结果有什么样的影响?
- 对于这些学习的数据集,所有数据混杂在一起学习?还是需要做隔离操作(即对不同的分类与设备,各自独立学习与预测)?它们会对预测有什么样的影响?
- 工作日与节假日对请求数值变化有什么影响?工作时间与休息时间对请求数值变化有什么影响?需要区分吗?而工作日与工作日大家的操作是否也会有所不同呢?如果只将日期分为工作日与节假日两种类型,那么对于所有工作日的预测结果是否都是一样的呢?
- 实际请求突然爆发式增长,而预测结果在正常值范围时,如何及时进行调节适应?将预测取值随爆发量变化处于合适水平?
- 对于请求数忽高忽低的非平滑曲线变化,如何能预测到合理范围?
- 对于诸多的特征参数,这些值应该如果设置?每个值对预测结果有什么影响?怎么进行调配?如何找到合适的参数设置搭配?
- 对于预测结果,需要有独立的字段用来记录。预测效果的展示,也需要进行对应的处理,将实际结果与预测结果进行区别。
对于这些问题,我们可以做如下处理:
- 由于我们要预测的是请求数的变化,而这个变化它可能是忽高忽低的,非线性的,所以我们可以选择岭回归算法来进行预测
- 对于属于监督类型的回归算法,我们需要提供的是可以计算的数值类型的学习数据,以及这些数据对应的标签值
- 虽然“日志请求统计汇总表”已经有不少特征字段存在了,但实际上它们的数据类型包括日期、数值与字符类型,并不能直接用于计算,需要根据需要对它们进行转换操作。
- 对于日期型数据是不能直接使用的,因为日期只不过代表时间的变化,而实际上不同的日期却有着不一样的意义,比如节假日与调休,大家放假了请求数自然就会与工作日不一样,为了方便数据导出计算需要增加周工作日字段(weekdays),用来存储对应的星期几数值,区分节假日与工作日。
- 对于周工作日字段(weekdays)这个特征参数,这个值的变化范围为0~6之间,是否直接使用这个值?直接使用会带来什么影响?这是需要认真思考的问题。因为直接使用0至6的数值,这样的数值模型的变化,实际结果会导致各个数据之间的权重关系的不同,一般来说值越大权重也越大,最终会直接影响预测结果。而在实际项目中,周一至周日,他们在权重上应该都是持平的一致的,只是各自标识不同日期时间而已。所以在转为机器学习数据时,可以转化为[0, 0, 0, 0, 0, 0]这样的特征码(节假日变化并不大,可以合并为1个标识,当然也可以分开设置,这个大家根据自己的设计思路进行修改即可),根据星期几的不同,在对应的位置标识为1,即周一为[1, 0, 0, 0, 0, 0],周二为[0, 1, 0, 0, 0, 0],以此类推,而节假日、调休,则为[0, 0, 0, 0, 0, 1]。
- 为了压缩单次学习数据的数量,隔离不同设置的请求量变化的相互影响,在生成学习数据时,可以将汇总统计和防火墙设备分离出来,各自独立学习与预测。
- 对于预测结果,需要新增预测总请求数(calculate_request_for_total)、预测总IP数(calculate_ip_for_total)两个字段
- 对于其他的问题思考解答,会在下面的实操部分分开讲解。
当然,除了这些,实际在开发中,还可能会遇到很多其他的各种问题或难点,需要机器学习算法设计人员更深入的了解业务,了解各种机器学习算法,了解各算法在实际项目中怎么灵活应用,熟练掌握特征的各种处理办法与转换方法,熟悉各参数的调配与测试,从中找出最优的解决方案。
4)编码实现
由于数据已经有了,所以只需要根据日期同步更新对应的周工作日字段(weekdays)即可,直接跳过数据清洗阶段
数据加工
数据加工主要是数据从数据库中读取出来,然后根据岭回归算法所要求的数据格式进行处理,组合成学习数据集与标签集,来进行学习训练。同时准备好预测数据,利用训练结果,预测出目标值。具体代码如下:\
def get_ml_weekdays(weekdays, value): """ 初始化周工作日字段特征标识 :param weekdays: 星期几,周一至周五值为0~4,节假日值为7 :param value: 默认标识值 """ # 初始化周工作日特征标识数组 week = [0, 0, 0, 0, 0, 0] # 为了避免对象引用问题,使用对象复制出一个副本来设置 _week = week.copy() # 如果是节假日,则设置数组索引为最后一个标识 if weekdays == 7: weekdays = 5 # 设置周工作日特征标识值,该参数可以用来调节预测值的匹配程度 _week[weekdays] = value return _week def calculate(now, tag, devname, is_all_day=False): """ 预测防火墙每小时请求数与Ip数 :param now: 预测日期 :param tag: 预测标签类型(total=汇总数据,device=指定各防火墙设备分类) :param devname: 防火墙设备名称 :param is_all_day: 是否预测全天各时间段的变化结果 """ # 设置查询起始时间,即学习数据集的时间范围为1个月内的记录 start_date = datetime_helper.timedelta('d', now, -31).date() # 获取当前预测日期为星期几(节假日值为7) weekdays = datetime_helper.get_weekdays(now) # 循环遍历1天24小时 for i in range(24): # 判断是否需要预测整天所有时间段的数据,如果为否,则直接跳过已过的时间,只对未到来的时间进行预测 if not is_all_day and i < now.hour: continue # 限制查询数据范围,只查询当前预测时间前后1小时内的数据,即对0点做预测时,只使用23点到凌晨1点的数据,以此类推 # 主要用于对学习数据进行隔离,增加预测数据的变化,不然会挠乱预测判断,导致最终预测出的结果是一个线性值 if i == 0: hour = '23,0,1' elif i == 23: hour = '22, 23, 0' else: hour = '{},{},{}'.format(i - 1, i, i + 1) # 设置sql查询语句 sql = """ select * from firewall_log_request_report_for_hour where date>='{}' and tag='{}' and devname='{}' and hour in ({}) order by date, hour """.format(start_date, tag, devname, hour) # 从数据库中获取学习数据集 flrr = firewall_log_request_report_for_hour_logic.FirewallLogLogic() result = flrr.select(sql) if not result: continue # 初始化机器学习特征集和标签集 ml_data = [] ml_label_request = [] ml_label_ip = [] # 遍历数据,设置周工作日特征标识,添加学习特征集 for model in result: # 因为查询出来的学习数据集,包含当前未发生的数据,这些数据的请求数为0,需要直接过滤掉,不然会干扰预测结果 if model.get('date').date() == now.date() and now.hour - 1 <= model.get('hour') and model.get('request_for_total') == 0: continue # 判断当前记录是否是当前需要预测日期,是的话将其周工作日字段值设置为1 if model.get('date').date() == now.date(): _week = get_ml_weekdays(model.get('weekdays'), 1) # 非当前预测日期的所有历史数据,都设置为0.5,即将其权重调低, # 用于弱化历史数据对预测日期的影响,只抽取历史日期中数据的变化规律, # 加强预测日期当天的数值强度,使其能应对请求数突发性爆发式增长或降低时,缩小预测值与实际发生数值的差距 else: _week = get_ml_weekdays(model.get('weekdays'), 0.5) # 将当前时间(小时)与周工作日特征参数组合成机器学习数据 # 例如周二凌晨1点的数据为:[1, 0, 1, 0, 0, 0, 0] _arr = [model.get('hour')] _arr.extend(_week) # 将机器学习数据添加到学习数据集中 # [[0, 0, 1, 0, 0, 0, 0] # [1, 0, 1, 0, 0, 0, 0] # [2, 0, 1, 0, 0, 0, 0] # ...] ml_data.append(_arr) # 将总请求数与总ip数添加到标签(答案)集中 ml_label_request.append(model.get('request_for_total')) ml_label_ip.append(model.get('ip_for_total')) # 设置预测数据 # 预测2020年1月15日早上8点的请求数,测试数据格式为:[8, 0, 0, 1, 0, 0, 0] calculate_data = [i] calculate_data.extend(get_ml_weekdays(weekdays, 1))
上面代码有几个关键地方需要留意的
1.查询数据范围限制代码
if i == 0: hour = '23,0,1' elif i == 23: hour = '22, 23, 0' else: hour = '{},{},{}'.format(i - 1, i, i + 1)
在代码注释中已经详细说明了限制的目的,主要用于对学习数据进行隔离,增加预测数据的变化,如果去掉这一段代码,将所有时间段内的数据加载出来提供给算法进行学习,预测结果就会出现下图的状态,各时间段内的数据会挠乱预测判断,导致最终预测出的结果是一个线性值。
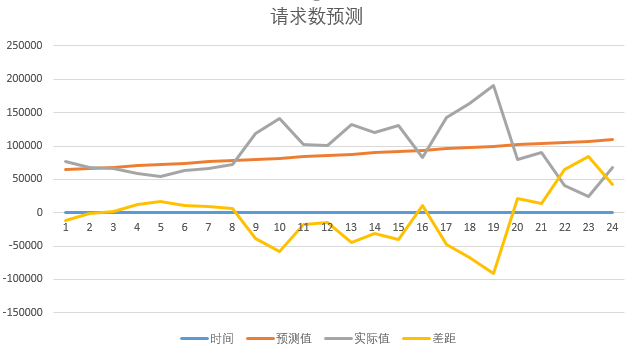
2.数据增加权重配置
# 判断当前记录是否是当前需要预测日期,是的话将其周工作日字段值设置为1 if model.get('date').date() == now.date(): _week = get_ml_weekdays(model.get('weekdays'), 1) # 非当前预测日期的所有历史数据,都设置为0.5,即将其权重调低, # 用于弱化历史数据对预测日期的影响,只抽取历史日期中数据的变化规律, # 加强预测日期当天的数值强度,使其能应对请求数突发性爆发式增长或降低时,缩小预测值与实际发生数值的差距 else: _week = get_ml_weekdays(model.get('weekdays'), 0.5)
未加权重配置时,算法训练会在全部数据集中寻找规律,然后根据历史数据来预测当前的数据变化,然后实际项目中会存在很多意外的事情发生,可能在某个时间段因为某些特定的原因,请求数爆增或爆跌,这时预测值与实际值之间就会存在很大的差距,有时这个差距会扩大到几倍、甚至十几倍都有可能,而实时查看图表时,实际值与预测值之间会有及大的落差。
而通过给当天的数据配置更高的权重,会让这些数据从算法运算中脱颖而出,让实际发生的数值与预测值在量上处于同一级别,而历史的大量数据则用来给算法训练出其历史变化规律,从而让预测结果更加趋向真实值,从而提高预测准确率。
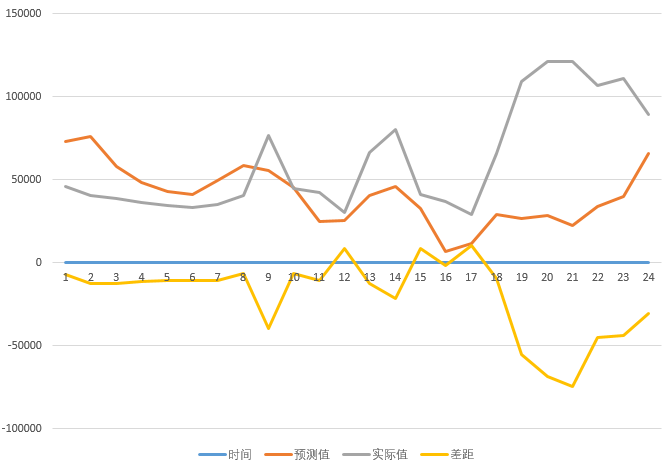
使用岭回归算法,对目标进行预测
前面已将训练数据集、训练标签集和预测数据加工处理好了,接下来就是调用回归算法函数,对训练数据集进行学习,然后预测目标结果。最后将结果更新到数据库中。
# 调用回归算法操作类的预测函数,预测总请求数 request_value = regression_helper.calculate(ml_data, ml_label_request, calculate_data) # 判断返回值是否正常(不为nan),并做非负值判断 if not numpy.isnan(request_value) and request_value.A[0][0] > 0: # 记录预测结果 request_value = request_value.A[0][0] else: request_value = 0 # 调用回归算法操作类的预测函数,预测总ip数 ip_value = regression_helper.calculate(ml_data, ml_label_ip, calculate_data) # 判断返回值是否正常(不为nan),并做非负值判断 if not numpy.isnan(ip_value) and ip_value.A[0][0] > 0: # 记录预测结果 ip_value = ip_value.A[0][0] else: ip_value = 0 # 同步更新数据库,记录当前预测结果 _flrr = firewall_log_request_report_for_hour_logic.FirewallLogLogic() fields = { 'date': string(now.date()), 'hour': i, 'tag': string(tag), 'devname': string(devname), 'weekdays': weekdays, 'calculate_request_for_total': request_value, 'calculate_ip_for_total': ip_value } wheres = 'date=\'{}\' and hour={} and tag=\'{}\' and devname=\'{}\''.format(now.date(), i, tag, devname) model = _flrr.get_model_for_cache_of_where(wheres) # 判断当前记录是否存在,存在则更新,不存在则新增 if model: _flrr.edit_model(model.get('id'), fields) else: _flrr.add_model(fields)
机器学习岭回归算法操作类代码(regression_helper.py)
岭回归算法函数直接根据《机器学习实战》书中的代码改造来的,详细请看注释。
def calculate(ml_data, ml_label, calculate_data): """ 岭回归算法预测函数 :param ml_data: 训练数据特征集(样本的特征数据) :param ml_label: 训练数据特征标签集,即每个样本对应的类别标签,目标变量,实际值 :param calculate_data: 预测数据 :return: 预测结果值 """ ws = ridge_regres(ml_data, ml_label) if (isinstance(ws, float) or isinstance(ws, numpy.float64)) and (numpy.isnan(ws) or numpy.isnan(ws[0][0])): return numpy.nan # 将预测数据转为矩阵 calculateMat = numpy.mat(calculate_data) # 将训练数据集转为矩阵 xMat = numpy.mat(ml_data) # 计算 xMat 平均值 xMeans = numpy.mean(xMat, 0) # 计算 X 的方差 xVar = numpy.var(xMat, 0) # 预测特征减去xMat的均值并除以方差 calculateMat = (calculateMat - xMeans) / xVar # 计算预测值 calculate_result = calculateMat * numpy.mat(ws).T + numpy.mean(ml_label) return calculate_result def ridge_regres(ml_data, ml_label): """ 岭回归求解函数,计算回归系数 :param ml_data: 训练数据特征集(样本的特征数据) :param ml_label: 训练数据特征标签集,即每个样本对应的类别标签,目标变量,实际值 :return: 经过岭回归公式计算得到的回归系数矩阵 """ try: # 将训练数据集转为矩阵 xMat = numpy.mat(ml_data) # 将标签集转为行向量 yMat = numpy.mat(ml_label).T # 计算Y的均值 yMean = numpy.mean(yMat, 0) # Y的所有特征减去均值 yMat = yMat - yMean # 计算 xMat 平均值 xMeans = numpy.mean(xMat, 0) # 计算 X 的方差 xVar = numpy.var(xMat, 0) # 所有特征都减去各自的均值并除以方差 xMat = (xMat - xMeans) / xVar # 计算x的平方值 xTx = xMat.T * xMat # 岭回归就是在矩阵 xTx 上加一个 λI 从而使得矩阵非奇异,进而能对 xTx + λI 求逆 denom = xTx + numpy.eye(numpy.shape(xMat)[1]) * numpy.exp(-9) # 检查行列式是否为零,即矩阵是否可逆,行列式为0的话就不可逆,不为0的话就是可逆。 if numpy.linalg.det(denom) == 0.0: print("This matrix is singular, cannot do inverse") return # 求解取得回归系数 ws = denom.I * (xMat.T * yMat) return ws.T except Exception as e: # 当训练数据集中,某一列的值全部相同时,这一列求解会得出0值,而对这个值进行运算就会出现异常 return numpy.nan
预测结果展示
从下面两图预测结果曲线图的对比上看,总体预测结果与实际结果相差并不大,应对突发性的数量变化,预测会有偏差,这需要后续对算法再做进一步的优化调整。经过处理,当前算法也会根据上一小时的结果及时做出调整,调整下一小时的预测数值

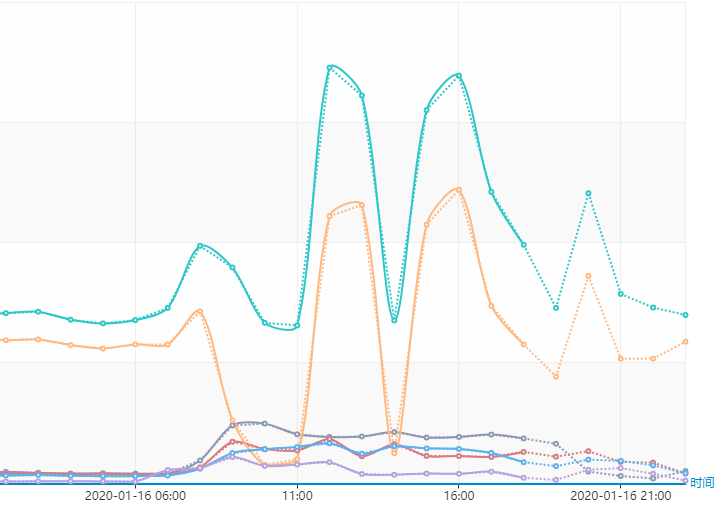
岭回归算法参数调优
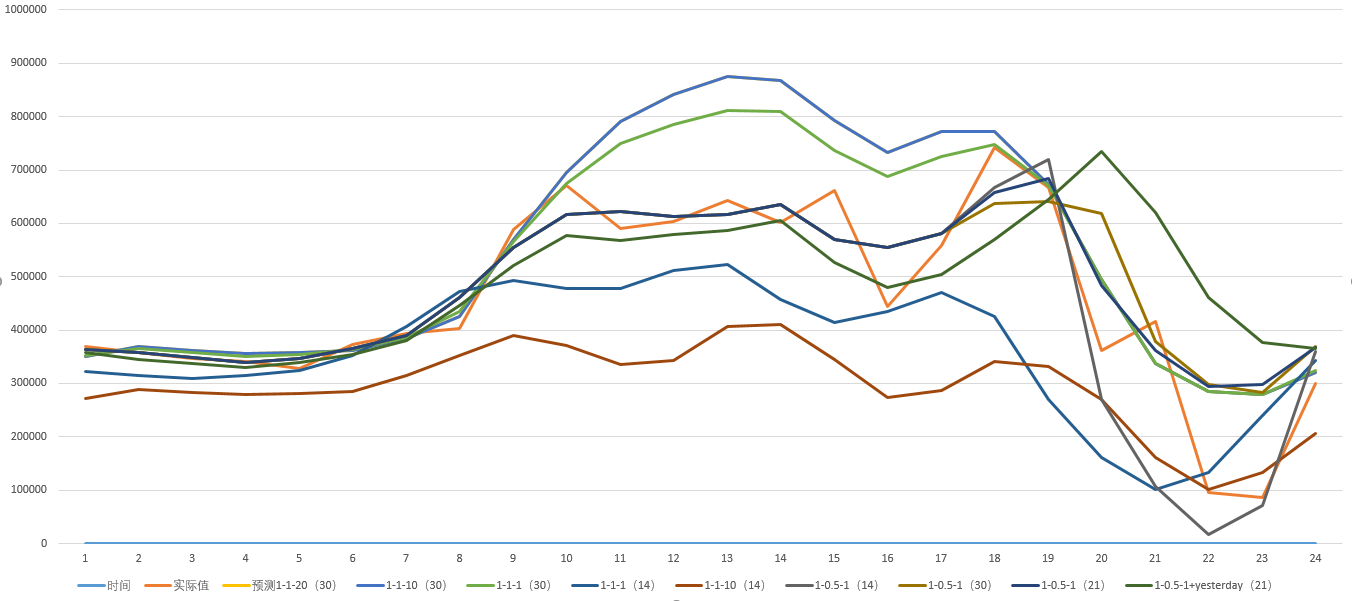
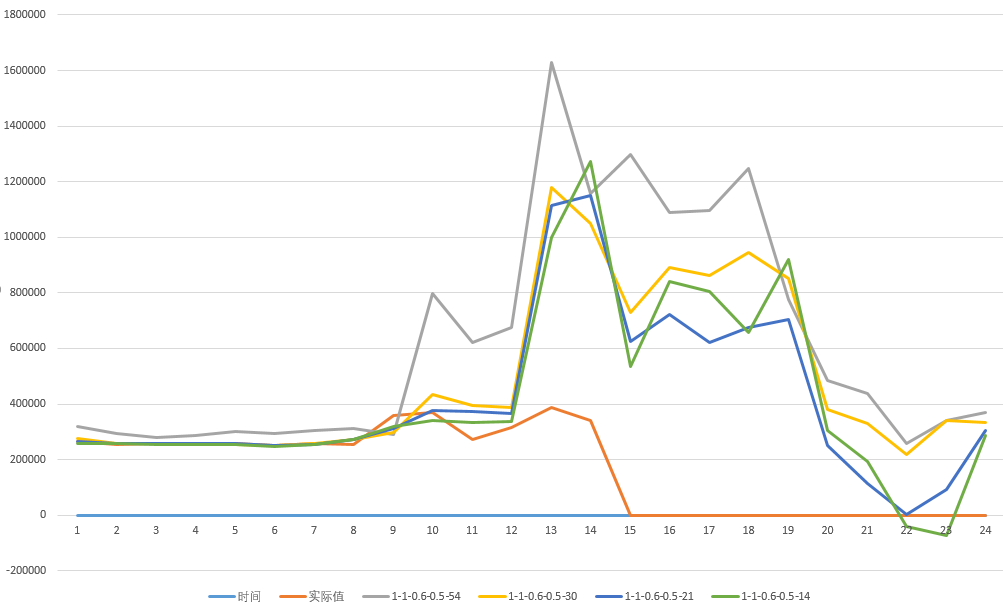
下图是在做岭回归算法调优时,不同参数下测试出来的预测结果
从图中可以看到,通过不同数据量、参数值大小、权重调整等参数的设置,预测结果曲线与实际结果曲线的偏差,再根据结果来设置最优参数值
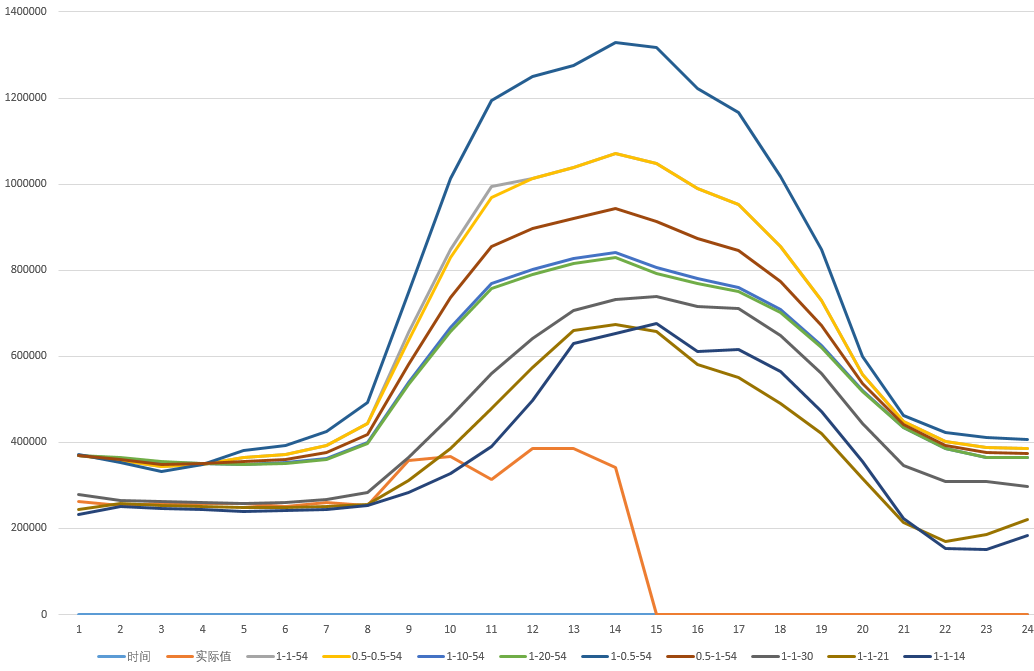
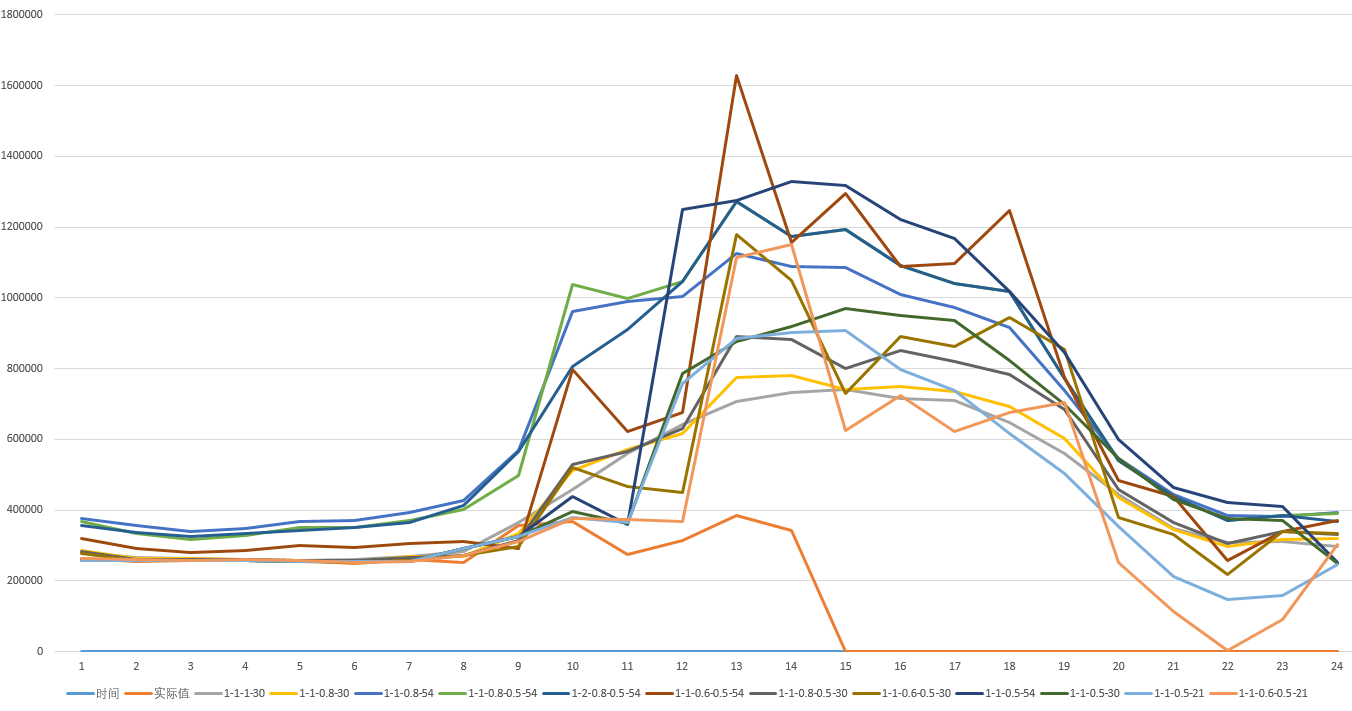



最终实现效果


4. 参考资料
https://github.com/apachecn/AiLearning/blob/master/docs/ml/8.回归.md




 浙公网安备 33010602011771号
浙公网安备 33010602011771号