Bellman_Ford 及其队列优化(SPFA)

设计背景

    (B)
    Richard Bellman，1958，DP
    Lester Ford Jr. 
    美国数学家，
    网络流，
    (S)
    段凡丁,1994，西南交通大学
    Shortest Path Faster Algorithm
    Bellman-ford最早的论文中曾提到过使用队列进行优化

---

过程模拟

• 设起点为s，

  dis[v]表示从s到v的最短路径，

  pre[v]为v的前驱节点，用来输出路径

  w[j]是边j的长度。

   1. 创建源顶点v到图中所有顶点的距离的集合dis，
       为图中的所有顶点指定一个距离值，
       初始均为Inf，源顶点距离为0；

   2. 计算最短路径，执行V-1次遍历；

   3. 对于图中的每条边：
        如果起点u的距离d加上边的权值w小于终点 v的距离d，
        则更新终点v的距离值d；

   4.检测图中是否有负权边形成了环，
        遍历图中的所有边，计算u至v的距离，
        如果对于v存在更小的距离，
        则说明存在环
   (无向图不能用这种方法判断负环)

• 初始化：

   　　dis[v]=∞(v≠s);dis[s]=0; pre[s]=0;

 

     for(int i=1; i<=n-1; i++)
        for(int j=1; j<=E; j++)
            if(dis[u]+w[j]<dis[v]){
                dis[v]=dis[u]+w[j];
                pre[v]=u;
            }

 

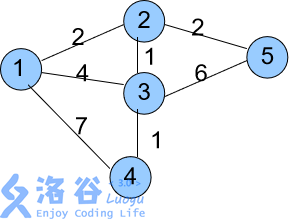
(又到了有图有真相的时候了)

(B)

         0. dis[1]=0; dis[2,3,4,5]=INF

         1. dis[1]=0,dis[2]=2,dis[3]=4,dis[4]=7,dis[5]=4

         2. dis[1]=0,dis[2]=2,dis[3]=3,dis[4]=4,dis[5]=4

         3. ...

         4. last round.

(S)

        Q={1} d[1...5]={0, INF, INF, INF， INF}

        Q={2,3,4} d[1...5]={0, 2, 4, 7, INF}

        Q={3,4,5} d[1...5]={0, 2, 3, 7, 4}

        Q={4,5} d[1...5]={0, 2, 3, 4, 4}

        Q={5} d[1...5]={0, 2, 3, 4, 4}

        Q={} d[1...5]={0, 2, 3, 4, 4}

        END.

---

代码实现

(B)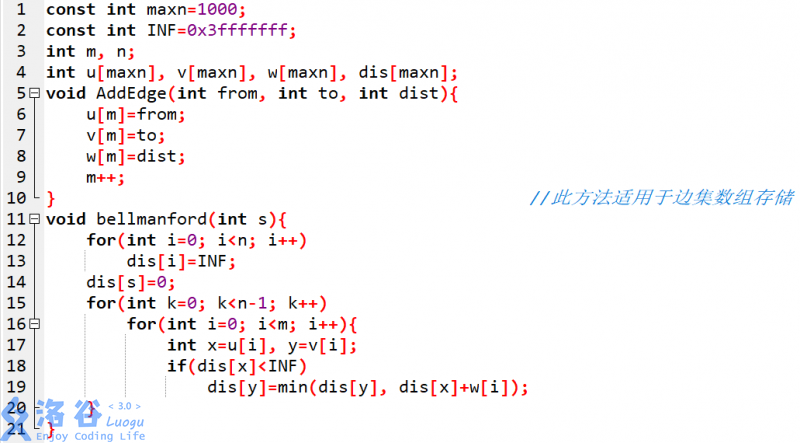

(S)

  void bellmanFord(int x)
    {
        for(int i=1; i<=n; i++)
            dis[i]=(i==x) ? 0 : INF;
        memset(v, 0, sizeof(v)); //inq
        queue<int> q;
        q.push(x);
        v[x]=1;
        while(!q.empty())
        {
            int from=q.front();
            q.pop();
            v[from]=0;
            for(edge * p=h[p]; p; p=p->next)
            {
                int to=p->to;
                int w =p->w;
                if(dis[from]+w<dis[to])
                {
                    dis[to]=dis[from]+w;
                    if(!v[to]) q.push(to), v[to]=1;
                }
            }
        }
    }

 

使用二维pre数组记录路径

---

所以说了这么多好像大家都知道的东西emmm

那么

Bellman_Ford与SPFA的整体策略都是通过边而松弛，

不断减小dis[x]的值

Bellman_Ford的思想是沿着最长的路径链(n-1)步进行优化dis[x]的值，

其中的很多操作是徒劳无益的

qwq

相较而言

SPFA利用队列动态更新最小值

    它所做的优化：

    1. 从起点开始沿路径链开始BFS，

       避免无益的松弛操作

    2.本质是优化了边松弛的顺序

    3. 当dis[x]被松弛小了应重新从x起BFS

---

emmm

第二篇博客就这么先结束吧；

希望自己可以慢慢进阶；

在这条路上越走越远~

你们也是~

今でもあなたは私の光。