Burnside引理&Pólya定理

Burnside's lemma

引例

题目描述

一个由2*2方格组成的正方形，每个格子上可以涂色或不涂色，

问共有多少种本质不同的涂色方案。

（若两种方案可通过旋转互相得到，称作本质相同的方案）

解法

每个格子可以涂色，可以不涂色，共有16种方案。将16种方案编号。

---

把本质相同的方案合并：

方案1：{1}，方案2：{2}，

方案3：{3,4,5,6}，方案4：{7,8,9,10}，

方案5：{11,12}，方案6：{13,14,15,16}，

共6种方案。

---

旋转可以看作是置换，所有置换组成置换群。

如果x通过某个置换可以变成y，说明x和y等价。

与x互相等价的一组元素组成了一个集合，称为x的等价类。

这个问题中，我们要求的就是这样的等价类有多少个。

我们由Burnside's lemma 可得

\[\begin{split} |X/G|&=|G|^{-1}\cdot \sum_{g\in G}|x^g|\\ 即\ 等价类的个数&=每个置换中不动元的个数和÷置换群的大小 \end{split} \]

对于该题，不动元为转动一定角度时，图形不发生变化，

不旋转，不动元16个，

逆时针90度，不动元2个{1,2}，

逆时针180度，不动元4个{1,2,11,12}，

逆时针270度，不动元2个{1,2}。

\[|X/G|=\frac {16+2+4+2}{4}=6 \]

---

Burnside's引理

\[\begin{split} |X/G|&=\frac 1{|G|}\sum_{g\in G}|x^g|\\ 等价类个数&=不动元个数的平均数 \end{split} \]

证明

\(X\)为16种情况，\(X/G\)为6种方案，\(G\)为旋转？度，

\(x\)为其中一种方案，\(|g_x|\)为\(G\)中旋转？度后使\(x\)方案中的情况不变的度数的个数。

---

考虑一个等价类，有

\[|x||g_x|=|G|,x\in X/G \]

其中，\(x\)为\(X\)的一个等价类，\(|g_x|\)为使它不发生改变的置换个数，

\(G\)为总置换个数，\(X/G\)为\(X\)在\(G\)置换群下的等价类的集合。

可以感性认知，对于一个等价类，有\(|g_x|\)种使它不发生改变的置换，

因为对于等价类\(x\)，本质不同的置换可以其中一个元素变为其他任意元素，所以有\(|x|\)种。

本质不同的置换个数×不变的置换个数=总置换个数。

---

考虑枚举每一个等价类，有

\[\sum_{x\in X/G}|x||g_x|=|G|\cdot|X/G| \]

每一个等价类对右式的贡献为\(|G|\)，共\(|X/G|\)个。

---

考虑交换枚举顺序，有

\[\sum_{x\in X}|g_x|=\sum_{g\in G}|x^g| \]

其中\(x\)指\(X\)的一个元素，\(|g_x|\)为使它不发生改变的置换个数，

此处的\(|g_x|\)与上面相同，因为同一个等价类\(|g_x|\)一定相同。

等式右半部分\(g\)为\(G\)中的一个置换，\(|x^g|\)为在该置换下不发生改变的元素个数。

---

由于\(\sum\limits_{x\in X/G}|x|\)可以等价于枚举完所有的元素，有

\[\begin{split} |G|\cdot |X/G|&=\sum_{x\in X/G}|x||g_x|(x指等价类)\\ &=\sum_{x\in X}|g_x|（x指元素）\\&=\sum_{g\in G}|x^g| \end{split} \]

应用

题目描述

一条含\(n\)颗珠子的项链，珠子的颜色有\(m\)种。

每种颜色的珠子个数为\(a_i\) \((a_1+a_2+\cdots+a_m=n)\)，求不同项链的种数。

解法

我们定义\(K\)循环为形如

\[\begin{pmatrix}a_1,a_2,\cdots,a_n\\a_{k+1},a_{k+2},\cdots,a_{k}\end{pmatrix} \]

的循环

对于一个\(K\)循环，经过\(\frac{lcm(n,k)}{k}\)后可以变回原来的项链。

---

\[\frac{lcm(n,k)}{k}=\frac n{gcd(n,k)} \]

这是循环节的大小，且每个循环节大小相等，

---

对于一个\(n\)个元素可重集合，

设\(p\)为每种元素的个数，满足\(p_1+p_2+\cdots+p_m=n\)，排列数有

\[A=\frac{(\sum\limits_{i=1}^mp_i!)}{\prod\limits_{i=1}^m(p_i!)} \]

就这道题而言，

对于一个\(K\)循环，我们有每种颜色的循环节个数为

\[\frac {a_i}{\frac {n}{gcd(n,k)}} \]

则由这些循环节组成的总方案数等同于排列数

\[ans=\frac{n!}{\prod_{i=1}^m\frac {a_i}{\frac {n}{gcd(n,k)}}} \]

又因为对于一个给定的\(d\)，使\(gcd(n,k)==d\)的\(k\)有\(\varphi(\frac nd)\)个

\[\begin{split} ans&=\frac{n!}{\prod_{i=1}^m\frac {a_i}{\frac {n}{gcd(n,k)}}}\\ &=\sum_{d|n}\varphi(\frac nd)\frac{n!}{\prod_{i=1}^m\frac {a_i\cdot d}{n}} \end{split} \]

Pólya enumeration theorem

引例

题目描述

一条含\(n\)颗珠子的项链，珠子的颜色有\(m\)种，求不同项链的种数。

解法

我们定义\(K\)循环为形如

\[\begin{pmatrix}a_1,a_2,\cdots,a_n\\a_{k+1},a_{k+2},\cdots,a_{k}\end{pmatrix} \]

的循环

对于一个\(K\)循环，经过\(\frac{lcm(n,k)}{k}\)后可以变回原来的项链。

---

\[\frac{lcm(n,k)}{k}=\frac n{gcd(n,k)} \]

这是循环节的大小，且每个循环节大小相等，

所以，循环节的个数为

\[\frac{n}{\frac{n}{gcd(n,k)}}=gcd(n,k) \]

---

如果每个循环节中的元素颜色一样，这就是一个\(K\)循环下的不动元，

所以，不动元的个数和为

\[\sum_{i=1}^nm^{gcd(i,n)} \]

所以，由Burnside's引理得

\[\begin{split} 等价类的个数&=\frac 1n不动元的个数和\\ &=\frac 1n\sum_{i=1}^n m^{gcd(n,i)}\\ &=\frac 1n\sum_{d|n}\sum_{i=1}^nm^d[gcd(n,i)==d]\\ &=\frac 1n\sum_{d|n}\varphi(\frac nd)m^d \end{split} \]

这样，我们就成功用Burnside's引理推出了Pólya定理。

Pólya定理

\[|Y^X/G|=1/|G|\sum_{g\in G}|Y|^{c(g)} \]

翻译：

\[\begin{split} &染色方案数（等价类的个数）\\ =&\frac 1{珠子数（总置换数）}\sum_{对于每种置换} 颜色数（映射数）^{循环节数} \end{split} \]

---

比如这幅图

颜色数={不染色，染色}

G={逆时针90°，逆时针180°，逆时针270°，不转}。

90°：一个循环节，180°：两个循环节，270°：一个循环节，不转：四个循环节。

所以有

\[ans=\frac 14\cdot(2^1+2^2+2^1+2^4)=6 \]

应用

前置例题

首先看一道例题：

有\(m\)个循环节，且循环节长度分别为\(L_1,L_2,\cdots,L_m(L_1+L_2+\cdots+L_m=n)\)的n阶置换有多少种？

（设\(L_1≤L_2≤\cdots≤L_m\)）

---

子问题1：从n个数中选L个出来，可以组成多少个循环？

①：从n个数中选L个出来：\(C_n^L\)

②：可以组成多少个循环：\((L-1)!\)

\[∴①×②=\frac {n!}{L(n-L)!} \]

子问题2：若\(L_i!=L_j\)，答案为多少？

\[\begin{split} ans&=\frac{n!}{L_1(n-L_1)!}\cdot \frac{(n-L_1)!}{L_2(n-L_1-L_2)!}\cdots\\ &=\frac{n!}{L_1L_2L_3\cdots L_m} \end{split} \]

设\(B_i\)表示\(i\)阶循环的个数，这\(B_i\)个循环可以形成\(B_i!\)个排列，使答案重复

\[∴ans=\frac{n!}{(L_1L_2\cdots L_m)\cdot(B_1!B_2!\cdots B_{L_m}!)} \]

题目描述

给定一个N 个结点的无向完全图，

现在你可以用 M 种颜色对这个图的每条边进行染色，每条边必须染一种颜色。

若两个已染色的图，

其中一个图可以通过结点重新编号而与另一个图完全相同，

就称这两个染色方案相同。

现在问你有多少种本质不同的染色方法，输出结果 mod P。

N≤53,M≤1000，P 是一个大于N 的质数。

解法

我们可以先解决点置换的问题。

根据前置例题，我们只需对\(L_1,L_2,\cdots,L_m\)进行枚举即可。

枚举量大概\(329931\)。

现在，

如果可以把边的置换与点的置换联系在一起，

算出边置换的循环节数与\(L_1\cdots L_m\)的关系，

那么问题就解决了。

---

对于一个固定的点置换进行分析。

一条边连接的两个定点要么在同一个循环内，要么在两个不同的循环内。

我们可以分别讨论。

①：对于一个\(n\)阶点循环，其内部的边可以组成多少个边循环？

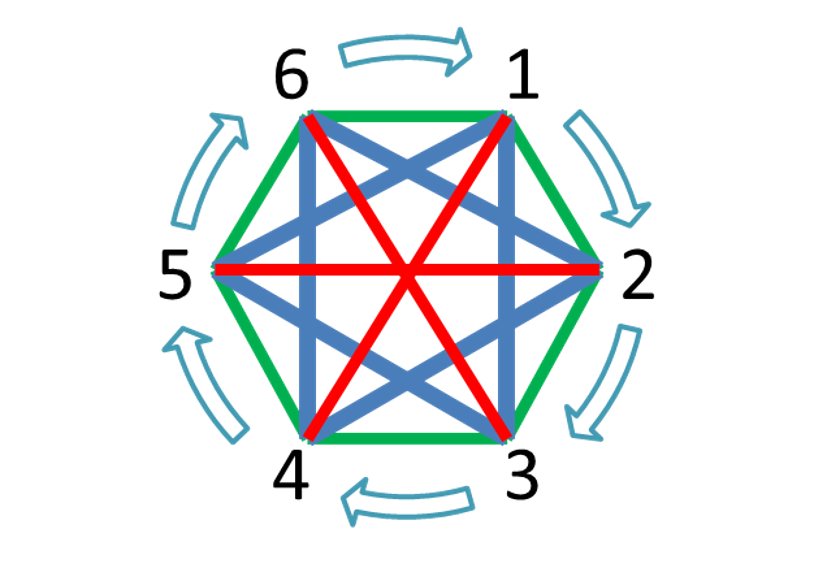
如图，

两点编号之差为\(1\)的边构成了一个循环，

两点编号之差为\(2\)的边构成了一个循环

······

两点编号之差为\(\lfloor\frac n2\rfloor\)的边构成了一个循环

如果位置号相差大于\(\lfloor\frac n2\rfloor\)，由于对称性，已经在之前讨论过了。

共\(\lfloor\frac n2\rfloor\)个循环。

②：不同循环的情况

两个循环间共有\(n\cdot m\)条边。

把两个循环分别看作两个齿轮，

对一条边来说，其左右端点同时移动，共\(\text{lcm}(n,m)\)条边。

即：等价类的大小=\(\text{lcm}(n,m)\)。

因为图是对称的，等价类等大，故等价类共有\(\frac {n\cdot m}{\text{lcm}(n,m)}=\gcd(n,m)\)个。

所以有\(\gcd(n,m)\)个循环节。

---

总置换数为\(\frac 1{n!}\)

对于每个\(L_1,\cdots,L_k\)，共有\(\frac{n!}{\prod_{i=1}^kL_i\prod_{i=1}^kB_i!}\)种置换，

对于每种置换，有\(\sum_{i=1}^k\lfloor\frac{L_i}{2}\rfloor+\sum_{i=1}^k\sum_{j=i+1}^k\gcd(L_i,L_j)\)个循环节。

所以：

\[\begin{split} ans=\frac 1{n!}\sum_{L_1,L_2\cdots,L_k}\frac{n!}{\prod_{i=1}^kL_i\prod_{i=1}^kB_i!}\cdot m^{\sum_{i=1}^k\lfloor\frac{L_i}{2}\rfloor+\sum_{i=1}^k\sum_{j=i+1}^k\gcd(L_i,L_j)} \end{split} \]

例题 from 毕克

Problem 1 环染色（Ring）——变式

题目描述

原题目就是Pólya定理的引例，这里是变式：

一个由 \(n(2 ≤ n ≤ 10^9)\) 个珠子组成的环，

我们要将所有珠子染成黑白两种颜色，但是黑色不能相邻，

问有多少种本质不同的方案，结果对 \(10^9 + 7\) 取模。

当两种方案通过旋转后变得相同时，我们认为他们本质相同。（不能翻转）

解法

设\(f_d\)表示不考虑本质相同，染一个长度为\(d\)的环的合法方案数。

对于置换\(K\)的环，由于其循环节个数为\(gcd(n,i)\)，所以其不动元个数为\(f_{gcd(n,i)}\)。

\[\begin{split} ans&=\frac 1n\sum_{i=1}^nf_{gcd(n,i)}\\ &=\frac 1n\sum_{d|n}\varphi(\frac nd)f_d \end{split} \]

由我也推不出来的方法得：

\[f_1=1,f_2=3,f_i=f_{i-1}+f_{i-2} \]

Problem 2 面染色（Face）

题目描述

一个由 \(n \cdot m\) 的矩形，我们要用他非常正常地密铺整个平面，

我们要将所有格子染成 \(c\) 种颜色。

问有多少种本质不同的方案，结果对 \(10^9 + 7\) 取模。

当两种方案看起来一样时，即矩形通过循环平移时一样，我们认为他们本质相同。

\(1 ≤ n ≤ 10^9, 1 ≤ m ≤ 10^9, 1 ≤ c ≤ 10^9\)

解法

横向考虑，循环节大小为\(\frac n{\gcd(n,i)}\)；纵向考虑，循环节大小为\(\frac m{\gcd(m,j)}\)。

所以，总的循环节大小为\(\text{lcm}(\frac n{\gcd(n,i)},\frac m{\gcd(m,j)})\)。

由于每个循环节大小相等，且共有\(n\cdot m\)个元素。

所以，循环节的个数为\(\frac {n\cdot m}{\text{lcm}(\frac n{\gcd(n,i)},\frac m{\gcd(m,j)})}\)。

\[\begin{split} ans&=\frac 1{n\cdot m}\sum_{i=1}^n\sum_{j=1}^mc^{\frac {n\cdot m}{\text{lcm}(\frac n{\gcd(n,i)},\frac m{\gcd(m,j)})}}\\ &=\frac 1{n\cdot m}\sum_{a|n}\sum_{b|m}\varphi(\frac na)\varphi(\frac mb)c^{\frac {n\cdot m}{\text{lcm}(\frac na,\frac mb)}}\\ &=\frac 1{n\cdot m}\sum_{a|n}\sum_{b|m}\varphi(a)\varphi(b)c^{\frac{n\cdot m}{\text{lcm}(a,b)}} \end{split} \]

Problem 3 面染色（Face）——变式

题目描述

一个由 \(n \cdot m\) 的矩形，我们要用他非常正常地密铺整个平面，我们要将所有格子染成 \(c\) 种颜色。

输入 \(n, m, c\) 和一个长度为 \(c\)的排列 \(p\)。

问有多少种本质不同的方案，将第 \(i\) 种颜色替换为 \(p_i\) 之后看起来是一样的。

结果对 \(10^9 + 7\) 取模。

（因为会密铺整个平面，所以即使交换两种颜色，他看起来还是有可能和原先一模一样。）

换句话说，我们问有多少本质不同的方案，

满足交换颜色之后，存在一种平移方式和自己相等。

这句话中的本质不同是指两种方案如果通过平移可以互相得到那么我们算作一种 。

$1 ≤ n, m ≤ 10^9, 1 ≤ c ≤ 16 $

解法

\(p\)不是有用的，有用的是\(p\)中每个轮换的长度。

定义\(C(x)\)表示在循环节长度为\(x\)时可用的颜色数。

只有当轮换长度为\(x\)的因子时，该组轮换的颜色才能保证可以通过平移和自己相等。

所以

\[ans=\frac 1{n\cdot m}\sum_{a|n}\sum_{b|m}\varphi(a)\varphi(b)C(\text{lcm}(a,b))^{\frac{n\cdot m}{\text{lcm}(a,b)}} \]

Problem 4 羊毛（Wolle）

题目描述

一个由 \(n \cdot m\) 的矩形，我们要用他非常正常地密铺整个平面，我们要将所有格子染成 \(c\) 种颜色。

但是 B 君是一个色盲， B 君只能判断两种颜色是否相同，而无法判断出每种颜色具体是什么。

输入 \(n, m, c\)。问有多少种本质不同的方案，结果对 \(10^9 + 7\) 取模。

当两种方案看起来一样时，

即：矩形通过循环平移并将颜色重新标号后一样，

我们认为他们本质相同。

$1 ≤ n, m ≤ 10^9, 1 ≤ c ≤ 16 $

解法

由Burnside引理得

\[ans=\frac{对于每种置换的不动元的总和}{n\cdot m\cdot c!} \]

考虑枚举\(c\)的每种置换，此时就与上题答案相同。

考虑交换枚举顺序，枚举所有轮换的长度，也就是\(c\)的一个拆分。

对于每个拆分，我们可以用上题的方法计算答案\(ans'\)。

然后计算这个拆分对应的排列有多少个，用2.3应用中的前置例题的解法求解。

我们有

\[ans=\frac{\sum_{对于c的拆分}ans'\cdot 该拆分下的排列数}{n\cdot m\cdot c!} \]

\(16\)的拆分数只有\(231\)，可以接受。

Problem 5 Isomorphism（sgu282）

同2.3应用

Problem 6 最后一题（Letzte）

题目描述

B 君作为一个色盲，

对一个 \(n\) 个点的无向完全图所有的边进行染 \(m\) 种颜色，问有多少种本质不同的染色方法。

如果两个方案通过对点的重新标号，或者对颜色的重新标号，

可以变为相同的，那么我们认为他们本质相同。

$1 ≤ n ≤ 16, 1 ≤ m ≤ 16 $

解法

设Problem5的方法套上Problem3的\(C\)函数后计算出的答案为\(ans'\)

\(ans\)同Problem4