网络流最大流

基本概念

源点：起始点

汇点：目标点

流：从源点到汇点的一条路径

容量：每条管道允许通过的最大流量

流量：通过一条边的水的实际体积

最小割

最大流等于最小割

增广路

从起点到终点的一条路径

寻找从S到T的一条增广路：

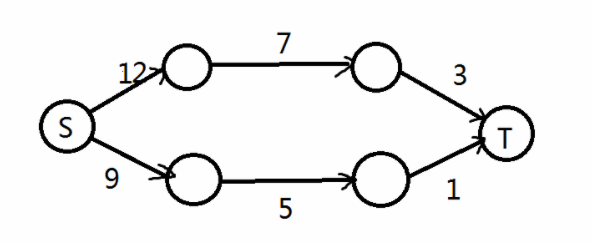
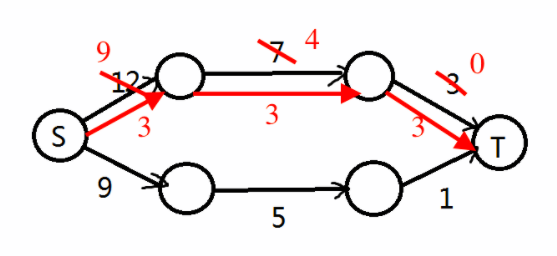
在红色的路线里，路径的一条最小流量是3，那么这条路径上的边都减去3，同时反向边加上3

这条增广路的一个流量是3

FF算法

传送门

\(O(n^2m)\)

1. 不断地进行寻找从起点到终点的一条增广路
2. 这条路上的边都减去这条增广路上的最小流量
3. 同时按照水流平衡，反向边加上最小流量
4. 直到没有增广路为止，最大流就是所有寻找增光路时得到最小流量之和

#include <iostream>
#include <cstdio>
#include <cstring>
#define ll long long
using namespace std;
const int N = 200 + 5;
const int M = 5e3 + 5;
int n, m, s, t;
struct Edge{
    int to, next, w;
}e[M << 1];
int head[N], tot = 1;
void add(int u, int v, int w){
    e[++tot].to = v;
    e[tot].w = w;
    e[tot].next = head[u];
    head[u] = tot;
}
bool vis[N];
int dfs(int u, int flow){ // 查找增广路
    if(u == t) return flow;
    vis[u] = 1;
    for(int i = head[u]; i; i = e[i].next){
        int v = e[i].to, w = e[i].w;
        if(w && !vis[v]){
            int t = dfs(v, min(flow, w));//获取这条增广路的最小流量
            if(t > 0) {
                e[i].w -= t;//减去这条流量
                e[i ^ 1].w += t;//反向边加上这个最小流量
                return t;
            }
        }
    }
    return 0;
}
ll FF(){
    ll max_flow = 0, res = 0;
    while(memset(vis, 0, sizeof(vis)) && (res = dfs(s, 2e9)) > 0){
        max_flow += res;
    }
    return max_flow;
}
int main(){
    scanf("%d%d%d%d", &n, &m, &s, &t);
    for(int i = 1; i <= m; i++){
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        add(u, v, w); add(v, u, 0);//有向图同时建立一条反向的边
    }
    printf("%lld\n", FF());
    return 0; 
}

DInic算法

时间复杂度\(O(n^2m)\)

可以看成常数很大的\(O(nm)\)

在FF算法基本上进行分层进行多路增光

1. 按照FF算法思维
2. 但首先进行BFS，得到起点出发到终点的一个分层情况。
3. 然后在DFS时，只需要按照分层的路径走即可
4. 同时在DFS时，如果说一个点到不了终点或无增广路，那么可以用分层的dis把结果这个点的路径进行切断，从而进行优化

DFS那也可以优化，搜索的次数越多，增广路的个数越少，所以可以到达终点就直接返回

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define ll long long
using namespace std;
const int N = 200 + 5;
const int M = 5e3 + 5;
int n, m, s, t;
struct Edge{
    int to, next, w;
}e[M << 1];
int head[N], tot = 1;
void add(int u, int v, int w){
    e[++tot].to = v;
    e[tot].w = w;
    e[tot].next = head[u];
    head[u] = tot;
}
int dis[N];
int dfs(int u, int flow){ //保证了每次DFS都能找到增广路
    if(u == t) return flow;
    int sum = 0;
    for(int i = head[u]; i; i = e[i].next){
        int v = e[i].to, w = e[i].w;
        if(w && dis[v] == dis[u] + 1){
            int t = dfs(v, min(flow, w)); //获取这条增广路的最小流量
            e[i].w -= t; e[i ^ 1].w += t;
            flow -= t; sum += t;
        }
    }
    if(!sum) dis[u] = 0; //结果u无法到达终点，或者没有增广路，切断经过这个点的路径
    return sum;
}
bool bfs(){ //分层判断是否有增广路
    memset(dis, 0, sizeof(dis));
    queue<int> q;
    q.push(s); dis[s] = 1;//分层
    while(!q.empty()){
        int u = q.front(); q.pop();
        for(int i = head[u]; i; i = e[i].next){
            int v = e[i].to, w = e[i].w;
            if(w && !dis[v]) {
                dis[v] = dis[u] + 1;
                q.push(v);
                if(v == t) return 1; //已经到达增广路
            }
        }
    }
    return dis[t];
}
ll Dinic(){
    ll max_flow = 0;
    while(bfs())
        max_flow += dfs(s, 2e9);
    return max_flow;
}
int main(){
    scanf("%d%d%d%d", &n, &m, &s, &t);
    for(int i = 1; i <= m; i++){
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        add(u, v, w); add(v, u, 0);
    }
    printf("%lld\n", Dinic());
    return 0; 
}

弧优化

每次进行bfs后，都是会从起点出发，如果说通过一条增广路时上的某个点还能得到一条增广路，那么进行dfs时路从该点出发而不是从起点出发。而且，对于一个点的有些边，如果流量不满足，但是dfs还是会去判断这些边，用还可以弧优化跳过一些无用的边。

从而进行弧优化

1. 按照Dinic算法
2. 创建一个cur[i]数组，表示从第i个点出发

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define ll long long
using namespace std;
const int N = 200 + 5;
const int M = 5e3 + 5;
int n, m, s, t;
struct Edge{
    int to, next, w;
}e[M << 1];
int head[N], tot = 1, cur[N]; //弧优化
void add(int u, int v, int w){
    e[++tot].to = v;
    e[tot].w = w;
    e[tot].next = head[u];
    head[u] = tot;
}
int dis[N];
int dfs(int u, int flow){ //保证了每次DFS都能找到增广路
    if(u == t) return flow;
    int sum = 0;
    for(int i = cur[u]; i && flow; i = e[i].next){
        cur[u] = i;
        int v = e[i].to, w = e[i].w;
        if(w > 0 && dis[v] == dis[u] + 1){
            int t = dfs(v, min(flow, w)); //获取这条增广路的最小流量
            e[i].w -= t; e[i ^ 1].w += t; //减去最小流量，同时反向边加上最小流量
            flow -= t; sum += t;
        }
    }
    if(!sum) dis[u] = 0;//结果u无法到达终点，或者没有增广路，切断经过这个点的路径
    return sum;
}
bool bfs(){//分层判断是否有增广路
    memset(dis, 0, sizeof(dis));
    queue<int> q;
    q.push(s); dis[s] = 1; cur[s] = head[s];//弧优化
    while(!q.empty()){
        int u = q.front(); q.pop();
        for(int i = head[u]; i; i = e[i].next){
            int v = e[i].to, w = e[i].w;
            if(w > 0 && !dis[v]) {
                cur[v] = head[v];// v这个点从head[v]出发是可行的
                dis[v] = dis[u] + 1;//分层
                q.push(v);
                if(v == t) return 1;//已经到达增广路，直接返回
            }
        }
    }
    return dis[t];
}
ll Dinic(){
    ll max_flow = 0;
    while(bfs())
        max_flow += dfs(s, 2e9);
    return max_flow;
}
int main(){
    scanf("%d%d%d%d", &n, &m, &s, &t);
    for(int i = 1; i <= m; i++){
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        add(u, v, w); add(v, u, 0);
    }
    printf("%lld\n", Dinic());
    return 0; 
}