java实现二叉树的Node节点定义手撕8种遍历(一遍过)

java实现二叉树的Node节点定义手撕8种遍历(一遍过)

用java的思想和程序从最基本的怎么将一个int型的数组变成Node树状结构说起，再到递归前序遍历，递归中序遍历，递归后序遍历，非递归前序遍历，非递归前序遍历，非递归前序遍历，到最后的广度优先遍历和深度优先遍历

1.Node节点的Java实现

首先在可以看到打上Node这个字符串，就可以看到只能的IDEA系统提供的好多提示：

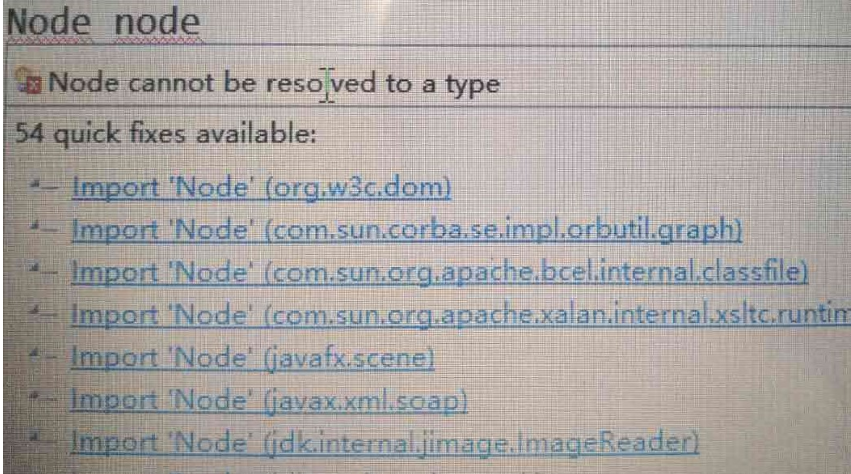
点进去看，却不是可以直接构成二叉树的Node，不是我们需要的东西。这里举个例子来看org.w3c.dom
这里面的Node是一个接口，是解析XML时的文档树。在官方文档里面看出：
该 Node 接口是整个文档对象模型的主要数据类型。它表示该文档树中的单个节点。
当实现 Node 接口的所有对象公开处理子节点的方法时，不是实现 Node 接口的所有对象都有子节点。

• 所以我们需要自定义一个Node类

package com.elloe.实现二叉树的Node节点.Node的Java实现;

import java.util.LinkedList;
import java.util.Stack;

/**
 * @author ElloeStudy(Sifa Zhang)
 * @create 2022-04-09 13:04
 * To: 真常应物，真常得性，常清常静，常清静矣
 *
 * 自定义Node的节点
 */
public class Node {
    private int value;    // 节点的值
    private Node node;   // 当前节点
    private Node left;  // 此节点的左节点，类型为Node
    private Node right; // 此节点的右节点，数据类型为Node

    public Node() {
    }

    public Node(int value) {
        this.value = value;
        this.left = null;
        this.right = null;
    }

    public int getValue() {
        return value;
    }

    public void setValue(int value) {
        this.value = value;
    }

    public Node getNode() {
        return node;
    }

    public void setNode(Node node) {
        this.node = node;
    }

    public Node getLeft() {
        return left;
    }

    public void setLeft(Node left) {
        this.left = left;
    }

    public Node getRight() {
        return right;
    }

    public void setRight(Node right) {
        this.right = right;
    }

    @Override
    public String toString(){
        return this.value + " ";
    }
}

2.数组升华二叉树

一般拿到的数据是一个int型的数组，那怎么将这个数组变成我们可以直接操作的树结构呢？

1、数组元素变Node类型节点
2、给N/2-1个节点设置子节点
3、给最后一个节点设置子节点【有可能只有左节点】

那现在就直接上代码:

public static void create(int[] datas, List<Node> list){
  // 将数组的数装换为节点Node
  for (int i = 0; i < datas.length; i++) {
    Node node = new Node(datas[i]);
    node.setNode(node);
    list.add(node);
  }

  // 节点关联树
  for (int index = 0; index < list.size()/2 - 1; index++) {
    //编号为n的节点他的左子节点编号为2*n 右子节点编号为2*n+1 但是因为list从0开始编号，所以还要+1
    list.get(index).setLeft(list.get(index * 2 + 1));
    list.get(index).setRight(list.get(index * 2 + 2));
  }

  // 单独处理最后一个节点，list.size()/2 -1 进行设置，避免单孩子情况
  int index = list.size()/2 - 1;
  list.get(index).setLeft(list.get(index * 2 + 1));
  if (list.size()%2 == 1){
    // 如果有奇数个节点，最后一个节点才有右节点
    list.get(index).setRight(list.get(index * 2 + 2));
  }
}

很细致的加上了很多的注释啊，所以保证一看就懂。

3.递归前序遍历

具体的原理没有什么好讲的，知道顺序即可

先序遍历过程：
（1）访问根节点；
（2）采用先序递归遍历左子树；
（3）采用先序递归遍历右子树；

这里用图来说明:

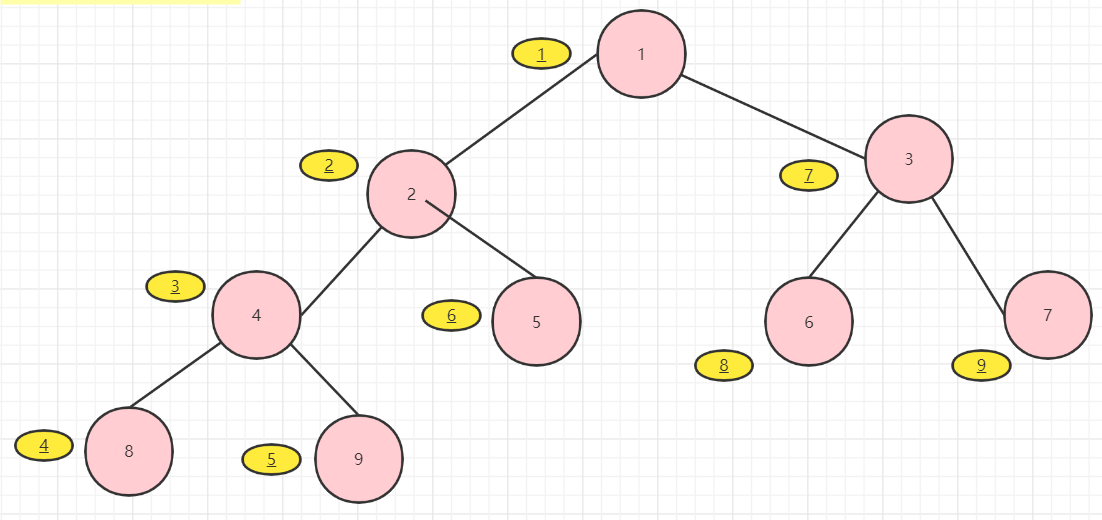
先序的结果：1 2 4 8 9 5 3 6 7

代码实现：

// 传入需要遍历的节点
public void preTraversal(Node node){
  // 当遇到叶节点，停止向下遍历
  if (node == null){
    return;
  }
  // 相当于点前节点的根节点的值
  System.out.print(node.getValue() + " ");
  // 先从底下依次遍历左节点
  preTraversal(node.getLeft());
  // 先从底下依次遍历右节点
  preTraversal(node.getRight());
}

看，说了很简单的！

4.递归中序遍历

中序遍历：
（1）采用中序遍历左子树；
（2）访问根节点；
（3）采用中序遍历右子树

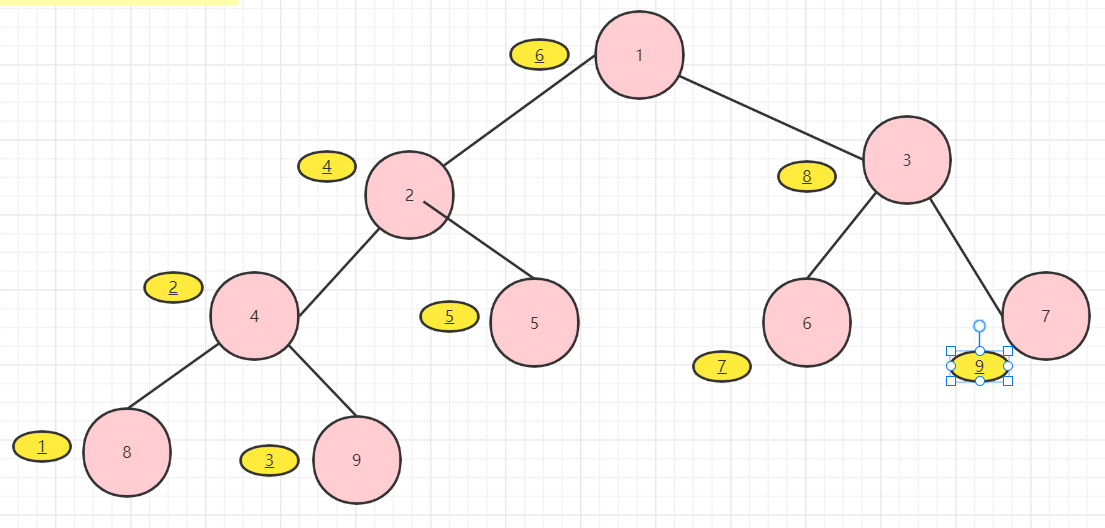
中序的结果：8 4 9 2 5 1 6 3 7

代码实现：

// 中序遍历（递归）
public void MidTraversal(Node node){
  // 判断当前节点是否为叶子节点，如果为叶子节点，停止遍历
  if (node == null){
    return;
  }
  // 获得左节点
  MidTraversal(node.getLeft());
  // 获得根节点
  System.out.print(node.getValue() + " ");
  // 获得右节点
  MidTraversal(node.getRight());
}

5.递归后序遍历

后序遍历：
（1）采用后序递归遍历左子树；
（2）采用后序递归遍历右子树；
（3）访问根节点；

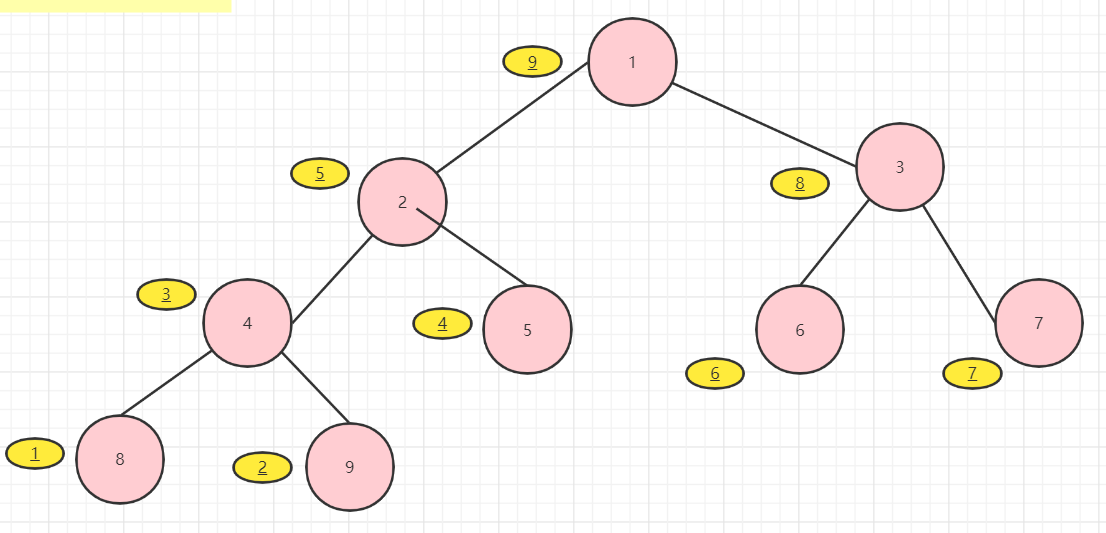
后序的结果：8 9 4 5 2 6 7 3 1

代码实现：

// 后序遍历（递归）
public void afterTraversal(Node node){
  if (node == null){
    return;
  }
  afterTraversal(node.getLeft());
  afterTraversal(node.getRight());
  System.out.print(node.getValue() + " ");
}

其实代码和思想一样，只是输出的位置和递归调用的位置不同而已。

个人觉得懂得非递归的原理和代码比懂递归更有意思，当你能手撕非递归二叉树遍历的时候，

面试官问你原理，还能不知道吗？

那接下来的三个模块就是非递归的三种遍历

拭目以待

6.非递归前序遍历

我这里使用了栈这个数据结构，用来保存不到遍历过但是没有遍历完全的父节点
之后再进行回滚。

基本的原理就是当循环中的present不为空时，就读取present的值，并不断更新present为其左子节点，

即不断读取左子节点，直到一个枝节到达最后的子节点，再继续返回上一层进行取值

代码：

// 非递归前序遍历
public void  beforeTraversalByLoop(Node node){
  // 创建栈保存遍历的节点,但又没有遍历完全的节点（即这个节点还没有操作完，临时保存一下）
  Stack<Node> stack = new Stack<>();
  Node present = node;  // 当前的节点
  while (present != null || !stack.isEmpty()){
    // 当前的节点不为null 且 栈不为空

    while (present != null){
      // 当 当前的节点不为null时，读取present的值,
      // 并不断更新present为其左子节点（不断读取左节点的值）

      // 读取根节点
      System.out.print(present.getValue() + " ");
      stack.push(present); // 将present压入栈（此时这个节点还没有操作好，临时保存）
      present = present.getLeft(); // 读取当前节点的左节点
    }

    if (!stack.isEmpty()){
      // 当栈不为空时
      present = stack.pop(); // 将临时保存的数取出
      present = present.getRight();  // 操作临时保存的节点的右节点（此时左节点已经全部读取好了）
    }
  }
}

先序的结果：1 2 4 8 9 5 3 6 7

7.非递归中序遍历

同原理

就是当循环中的present不为空时，就读取present的值，并不断更新present为其左子节点，

但是切记这个时候不能进行输出，必须不断读取左子节点，直到一个枝节到达最后的子节点，

然后每次从栈中拿出一个元素，就进行输出，再继续返回上一层进行取值。

代码实现：

// 非递归中序遍历
public void traversalMidByLoop(Node node) {
    // 创建栈保存遍历的节点,但又没有遍历完全的节点（即这个节点还没有操作完，临时保存一下）
    Stack<Node> stack = new Stack<>();
    Node present = node; // 当前操作的节点
    while (present != null || !stack.isEmpty()) {
        // 当前的节点不为null 且 栈不为空

        // 获取左节点
        while (present != null) {
            stack.push(present);// 将present压入栈（此时这个节点还没有操作好，临时保存）
            present = present.getLeft();// 读取当前节点的左节点
        }

        if (!stack.isEmpty()) {
            present = stack.pop();
            // 获取根节点
            System.out.print(present.getValue() + " ");
            present = present.getRight(); // 获取右节点
        }
    }
}

8.非递归后序遍历

后序遍历相比前面的前序遍历和中序遍历在编程这里会难一点，不过理解了思想，看代码还是没有什么问题的

代码实现：

// 非递归后序遍历
public void traversalAfterByLoop(Node node){
    // 存放还没有完成操作的节点，临时储存
    Stack<Node> stack = new Stack<>();
    Node present = node; // 当前的操作节点
    Node prev = node;  // 先前的根节点（一个标志flag）

    while (present != null || !stack.isEmpty()){
        // 当前的节点不为null 且 栈不为空

        while(present != null){
            // 如果当前的节点不为空

            stack.push(present); // 将当前这个节点临时存储
            present = present.getLeft(); // 遍历获取其左节点
        }

        if (!stack.isEmpty()){
            // 拿出栈顶的值，并没有进行删除
            Node temp = stack.peek().getRight(); // 获取栈顶节点的右节点

            // 节点没有右节点或者到达根节点【考虑到了最后一种情况】
            if (temp == null || temp == prev){
                present = stack.pop();
                // 获取根节点
                System.out.print(present.getValue() + " ");

                prev = present;   // 将当前的节点作为 根节点的标志（flag）
                present = null;  // 将当前节点 设为空
            }else{
                // 节点有右节点 或者 没有到达根节点
                present = temp; // 将这个右节点设置为当前节点
            }
        }
    }
}

最后就可以放大招了，来看看广度优先遍历和深度优先遍历吧

9.广度优先遍历

在广度优先遍历里面我用到了队列，不明白的小伙伴可以看我的上一篇！

// 广度优先遍历
public void bfs(Node root){
    if (root == null) {
        return ;
    }

    LinkedList<Node> queue = new LinkedList<>();
    queue.offer(root); // 将根节点存入队列

    //当队列里有值时，每次取出队首的node打印，打印之后判断node是否有子节点，
    // 若有，则将子节点加入队列
    while (queue.size() > 0){
        Node node = queue.peek(); // 查看队列的头部节点，不会删除节点
        queue.poll(); // 取出（移除）对首的节点并打印
        System.out.print(node.getValue() + " ");
        if (node.getLeft() != null){
            // 如果有左节点，则将其存入队列
            queue.offer(node.getLeft());
        }
        if (node.getRight() != null){
            // 如果有右节点，则将其存入对列
            queue.offer(node.getRight());
        }
    }
}

10.深度优先遍历

在深度优先遍历里面我用到了栈，不明白的小伙伴可以看我的上一篇！

// 深度优先遍历
public void dfs(Node root) {
    if (root == null){
        return;
    }

    Stack<Node> stack = new Stack<>();
    stack.push(root); // 将根节点压入栈里面

    while (!stack.isEmpty()){
        Node node = stack.pop(); // 弹出栈顶的节点
        System.out.print(node.getValue() + " ");

        // 深度优先遍历，先遍历左边在右边，所以先将右边压入再将左边压入
        if (node.getRight() != null){
            stack.push(node.getRight());
        }
        if (node.getLeft() != null){
            stack.push(node.getLeft());
        }
    }
}

11.测试用例（贴心吧😎）

public static void main(String[] args) {
    int[] ints = new int[9];

    for (int i = 0; i < ints.length; i++) {
        ints[i] = i + 1;
    }
    List<Node> nodes = new ArrayList<>();
    // 数组创建二叉树
    BinaryFromArray.create(ints,nodes);
    for (Node node : nodes){
        System.out.print(node.getValue() + " ");
        System.out.print(node.getNode() + " ");
        System.out.print(node.getLeft() + " ");
        System.out.println(node.getRight());
    }

    // 先序遍历（递归），从当前数组的第一个node节点开始
    nodes.get(0).preTraversal(nodes.get(0));
    // 中序遍历（递归），从当前数组的第一个node节点开始
    System.out.print("\r\n"); // \r\n    换行
    nodes.get(0).MidTraversal(nodes.get(0));
    // 后序遍历（递归），从当前数组的第一个node节点开始
    System.out.print("\r\n"); // \r\n    换行
    nodes.get(0).afterTraversal(nodes.get(0));
}

public static void main(String[] args) {
    int[] ints = new int[9];

    for (int i = 0; i < ints.length; i++) {
        ints[i] = i + 1;
    }
    List<Node> nodes = new ArrayList<>();
    // 数组创建二叉树
    BinaryFromArray.create(ints,nodes);
    for (Node node : nodes){
        System.out.print(node.getValue() + " ");
        System.out.print(node.getNode() + " ");
        System.out.print(node.getLeft() + " ");
        System.out.println(node.getRight());
    }

    // 先序遍历，从当前数组的第一个node节点开始
   nodes.get(0).beforeTraversalByLoop(nodes.get(0));
    // 中序遍历，从当前数组的第一个node节点开始
    System.out.println(" ");
   nodes.get(0).traversalMidByLoop(nodes.get(0));
    // 后序遍历，从当前数组的第一个node节点开始
    System.out.println(" ");
    nodes.get(0).traversalAfterByLoop(nodes.get(0));
}

public static void main(String[] args) {
    int[] ints = new int[9];

    for (int i = 0; i < ints.length; i++) {
        ints[i] = i + 1;
    }
    List<Node> nodes = new ArrayList<>();
    // 数组创建二叉树
    BinaryFromArray.create(ints,nodes);
    for (Node node : nodes){
        System.out.print(node.getValue() + " ");
        System.out.print(node.getNode() + " ");
        System.out.print(node.getLeft() + " ");
        System.out.println(node.getRight());
    }

    // 广度优先遍历
   nodes.get(0).bfs(nodes.get(0));
    // 深度优先遍历
    System.out.println();
    nodes.get(0).dfs(nodes.get(0));
}

12.全部代码（完整版）[前面成功的小伙伴可以直接跳过]

package com.elloe.实现二叉树的Node节点.Node的Java实现;

import java.util.LinkedList;
import java.util.List;
import java.util.Stack;

/**
 * @author ElloeStudy(Sifa Zhang)
 * @create 2022-04-09 13:04
 * To: 真常应物，真常得性，常清常静，常清静矣
 *
 * 自定义Node的节点
 */
public class Node {
    private int value;    // 节点的值
    private Node node;   // 当前节点
    private Node left;  // 此节点的左节点，类型为Node
    private Node right; // 此节点的右节点，数据类型为Node

    public Node() {
    }

    public Node(int value) {
        this.value = value;
        this.left = null;
        this.right = null;
    }

    public int getValue() {
        return value;
    }

    public void setValue(int value) {
        this.value = value;
    }

    public Node getNode() {
        return node;
    }

    public void setNode(Node node) {
        this.node = node;
    }

    public Node getLeft() {
        return left;
    }

    public void setLeft(Node left) {
        this.left = left;
    }

    public Node getRight() {
        return right;
    }

    public void setRight(Node right) {
        this.right = right;
    }

    @Override
    public String toString(){
        return this.value + " ";
    }

    // 构建二叉树
    public static void create(int[] datas, List<Node> list){
        // 将数组的数装换为节点Node
        for (int i = 0; i < datas.length; i++) {
            Node node = new Node(datas[i]);
            node.setNode(node);
            list.add(node);
        }

        // 节点关联树
        for (int index = 0; index < list.size()/2 - 1; index++) {
            //编号为n的节点他的左子节点编号为2*n 右子节点编号为2*n+1 但是因为list从0开始编号，所以还要+1
            list.get(index).setLeft(list.get(index * 2 + 1));
            list.get(index).setRight(list.get(index * 2 + 2));
        }

        // 单独处理最后一个节点，list.size()/2 -1 进行设置，避免单孩子情况
        int index = list.size()/2 - 1;
        list.get(index).setLeft(list.get(index * 2 + 1));
        if (list.size()%2 == 1){
            // 如果有奇数个节点，最后一个节点才有右节点
            list.get(index).setRight(list.get(index * 2 + 2));
        }
    }

    // 先序遍历（递归）
    // 传入需要遍历的节点
    public void preTraversal(Node node){
        // 当遇到叶节点，停止向下遍历
        if (node == null){
            return;
        }
        // 相当于点前节点的根节点的值
        System.out.print(node.getValue() + " ");
        // 先从底下依次遍历左节点
        preTraversal(node.getLeft());
        // 先从底下依次遍历右节点
        preTraversal(node.getRight());
    }


    // 中序遍历（递归）
    public void MidTraversal(Node node){
        // 判断当前节点是否为叶子节点，如果为叶子节点，停止遍历
        if (node == null){
            return;
        }
        // 获得左节点
        MidTraversal(node.getLeft());
        // 获得根节点
        System.out.print(node.getValue() + " ");
        // 获得右节点
        MidTraversal(node.getRight());
    }

    // 后序遍历（递归）
    public void afterTraversal(Node node){
        if (node == null){
            return;
        }
        afterTraversal(node.getLeft());
        afterTraversal(node.getRight());
        System.out.print(node.getValue() + " ");
    }


    // 非递归前序遍历
    public void  beforeTraversalByLoop(Node node){
        // 创建栈保存遍历的节点,但又没有遍历完全的节点（即这个节点还没有操作完，临时保存一下）
        Stack<Node> stack = new Stack<>();
        Node present = node;  // 当前的节点
        while (present != null || !stack.isEmpty()){
            // 当前的节点不为null 且 栈不为空

            while (present != null){
                // 当 当前的节点不为null时，读取present的值,
                // 并不断更新present为其左子节点（不断读取左节点的值）

                // 读取根节点
                System.out.print(present.getValue() + " ");
                stack.push(present); // 将present压入栈（此时这个节点还没有操作好，临时保存）
                present = present.getLeft(); // 读取当前节点的左节点
            }

            if (!stack.isEmpty()){
                // 当栈不为空时
                present = stack.pop(); // 将临时保存的数取出
                present = present.getRight();  // 操作临时保存的节点的右节点（此时左节点已经全部读取好了）
            }
        }
    }

    // 非递归中序遍历
    public void traversalMidByLoop(Node node) {
        // 创建栈保存遍历的节点,但又没有遍历完全的节点（即这个节点还没有操作完，临时保存一下）
        Stack<Node> stack = new Stack<>();
        Node present = node; // 当前操作的节点
        while (present != null || !stack.isEmpty()) {
            // 当前的节点不为null 且 栈不为空

            // 获取左节点
            while (present != null) {
                stack.push(present);// 将present压入栈（此时这个节点还没有操作好，临时保存）
                present = present.getLeft();// 读取当前节点的左节点
            }

            if (!stack.isEmpty()) {
                present = stack.pop();
                // 获取根节点
                System.out.print(present.getValue() + " ");
                present = present.getRight(); // 获取右节点
            }
        }
    }

    // 非递归后序遍历
    public void traversalAfterByLoop(Node node){
        // 存放还没有完成操作的节点，临时储存
        Stack<Node> stack = new Stack<>();
        Node present = node; // 当前的操作节点
        Node prev = node;  // 先前的根节点（一个标志flag）

        while (present != null || !stack.isEmpty()){
            // 当前的节点不为null 且 栈不为空

            while(present != null){
                // 如果当前的节点不为空

                stack.push(present); // 将当前这个节点临时存储
                present = present.getLeft(); // 遍历获取其左节点
            }

            if (!stack.isEmpty()){
                // 拿出栈顶的值，并没有进行删除
                Node temp = stack.peek().getRight(); // 获取栈顶节点的右节点

                // 节点没有右节点或者到达根节点【考虑到了最后一种情况】
                if (temp == null || temp == prev){
                    present = stack.pop();
                    // 获取根节点
                    System.out.print(present.getValue() + " ");

                    prev = present;   // 将当前的节点作为 根节点的标志（flag）
                    present = null;  // 将当前节点 设为空
                }else{
                    // 节点有右节点 或者 没有到达根节点
                    present = temp; // 将这个右节点设置为当前节点
                }
            }
        }
    }


    // 广度优先遍历
    public void bfs(Node root){
        if (root == null) {
            return ;
        }

        LinkedList<Node> queue = new LinkedList<>();
        queue.offer(root); // 将根节点存入队列

        //当队列里有值时，每次取出队首的node打印，打印之后判断node是否有子节点，
        // 若有，则将子节点加入队列
        while (queue.size() > 0){
            Node node = queue.peek(); // 查看队列的头部节点，不会删除节点
            queue.poll(); // 取出（移除）对首的节点并打印
            System.out.print(node.getValue() + " ");
            if (node.getLeft() != null){
                // 如果有左节点，则将其存入队列
                queue.offer(node.getLeft());
            }
            if (node.getRight() != null){
                // 如果有右节点，则将其存入对列
                queue.offer(node.getRight());
            }
        }
    }


    // 深度优先遍历
    public void dfs(Node root) {
        if (root == null){
            return;
        }

        Stack<Node> stack = new Stack<>();
        stack.push(root); // 将根节点压入栈里面

        while (!stack.isEmpty()){
            Node node = stack.pop(); // 弹出栈顶的节点
            System.out.print(node.getValue() + " ");

            // 深度优先遍历，先遍历左边在右边，所以先将右边压入再将左边压入
            if (node.getRight() != null){
                stack.push(node.getRight());
            }
            if (node.getLeft() != null){
                stack.push(node.getLeft());
            }
        }
    }
}

13.小结

• 以上的代码，全部为我自己成功实现的coding,希望看到这里的你，已经完全理清二叉树的遍历😛
• 继续努力！！！
• 参考文章：https://blog.csdn.net/weixin_42636552/article/details/82973190