基础算法问题
特别注意:动画来自https://blog.csdn.net/iechenyb/article/details/81941022?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param
| 排序算法 | 平均时间复杂度 | 空间复杂度 | 是否稳定 | |
|---|---|---|---|---|
| 冒泡排序 | O(n2) | O(1) | 是 | |
| 选择排序 | O(n2) | O(1) | 不是 | |
| 直接插入排序 | O(n2) | O(1) | 是 | |
| 归并排序 | O(nlogn) | O(nlogn) | 是 | |
| 快速排序 | O(nlogn) | O(logn) | 不是 | |
| 堆排序 | O(nlogn) | O(1) | 不是 | |
| 希尔排序 | O(nlogn) | O(1) | 不是 | |
注:
1 归并排序可以通过手摇算法将空间复杂度降到O(1),但是时间复杂度会提高。
1.冒泡排序
for (int i = 0; i < nums.Length-1; i++) { //交换的次数 for (int j = 0; j < nums.Length-1-i; j++) { if (nums[j] > nums[j + 1]) { temp = nums[j]; nums[j] = nums[j + 1]; nums[j + 1] = temp; } } }
2.选择排序
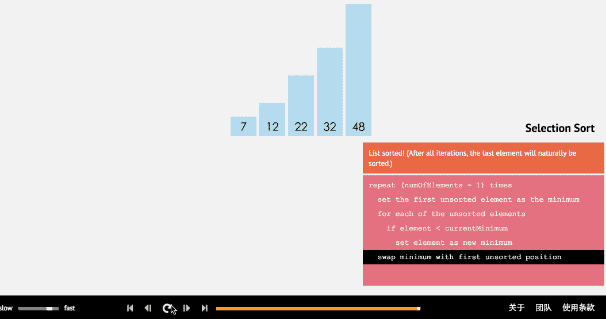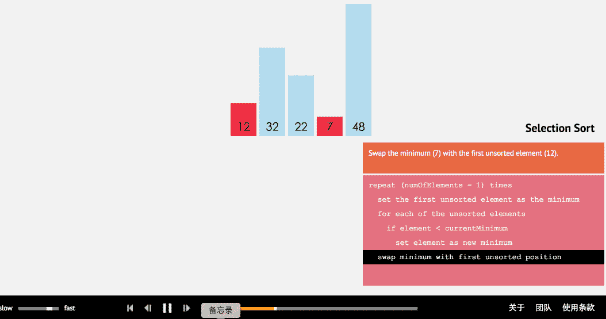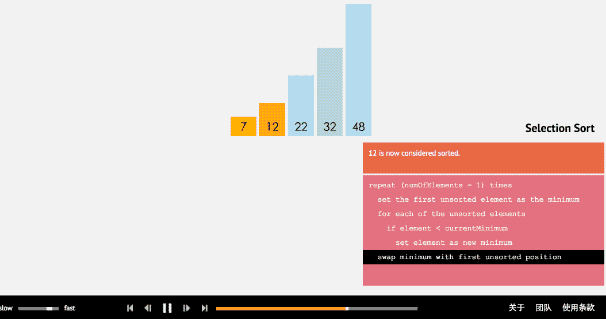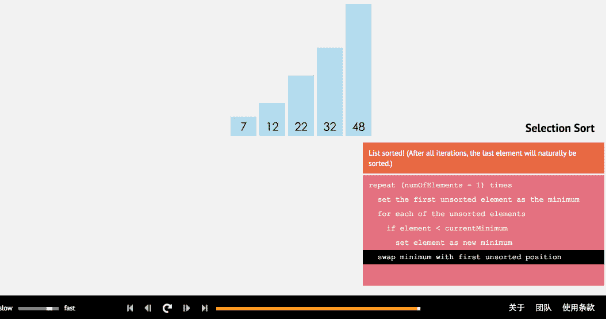
private static void SelectSort(int[] arr) { int temp = 0; for (int i = 0; i < arr.Length - 1; i++) { int minVal = arr[i]; //假设 i 下标就是最小的数 int minIndex = i; //记录我认为最小的数的下标 for (int j = i + 1; j < arr.Length; j++) //这里只是找出这一趟最小的数值并记录下它的下标 { //说明我们认为的最小值,不是最小 if (minVal > arr[j]) //这里大于号是升序(大于是找出最小值) 小于是降序(小于是找出最大值) { minVal = arr[j]; //更新这趟最小(或最大)的值 (上面要拿这个数来跟后面的数继续做比较) minIndex = j; //记下它的下标 } } //最后把最小的数与第一的位置交换 temp = arr[i]; //把第一个原先认为是最小值的数,临时保存起来 arr[i] = arr[minIndex]; //把最终我们找到的最小值赋给这一趟的比较的第一个位置 arr[minIndex] = temp; //把原先保存好临时数值放回这个数组的空地方, 保证数组的完整性 } }
3.快速排序
快速排序从小到大排序:在数组中随机选一个数(默认数组首个元素),数组中小于等于此数的放在左边,大于此数的放在右边,再对数组两边递归调用快速排序,重复这个过程。
void QuickSort(ref List<int> nums, int left, int right) { if (left < right) { int i = left; int j = right; int middle = nums[(left + right) / 2]; while (true) { while (i < right && nums[i] < middle) { i++; }; while (j > 0 && nums[j] > middle) { j--; }; if (i == j) break; int temp = nums[i]; nums[i] = nums[j]; nums[j] = temp; if (nums[i] == nums[j]) j--; } QuickSort(ref nums, left, i); QuickSort(ref nums, i + 1, right); } }
4.插入排序
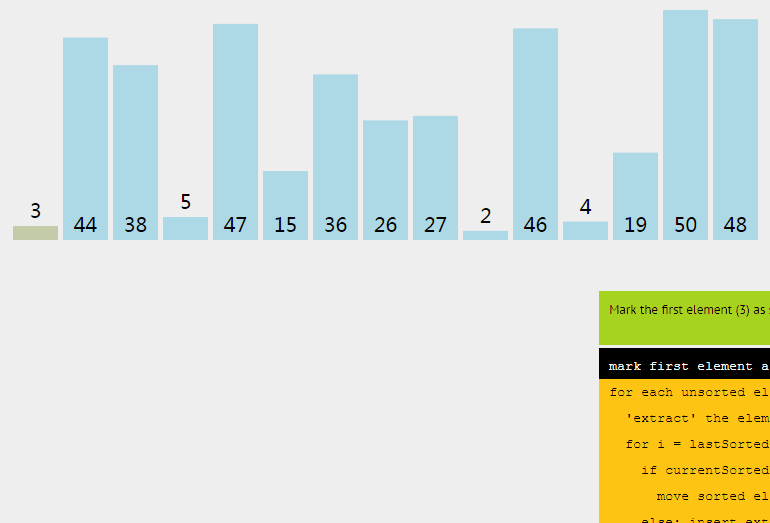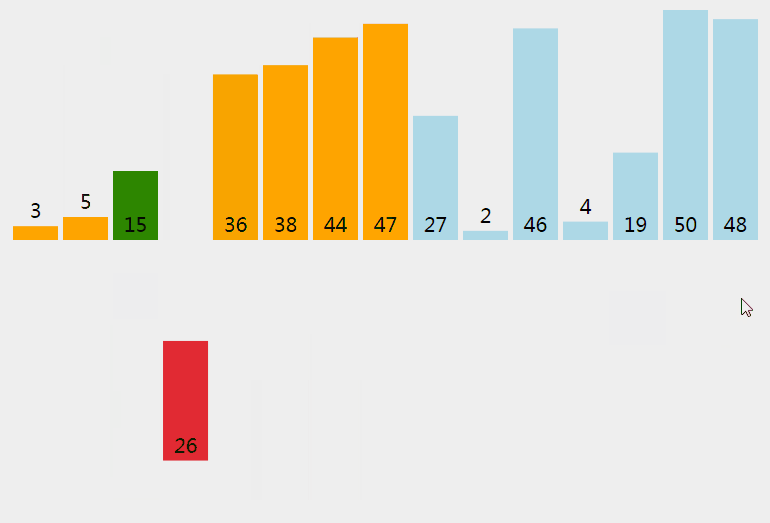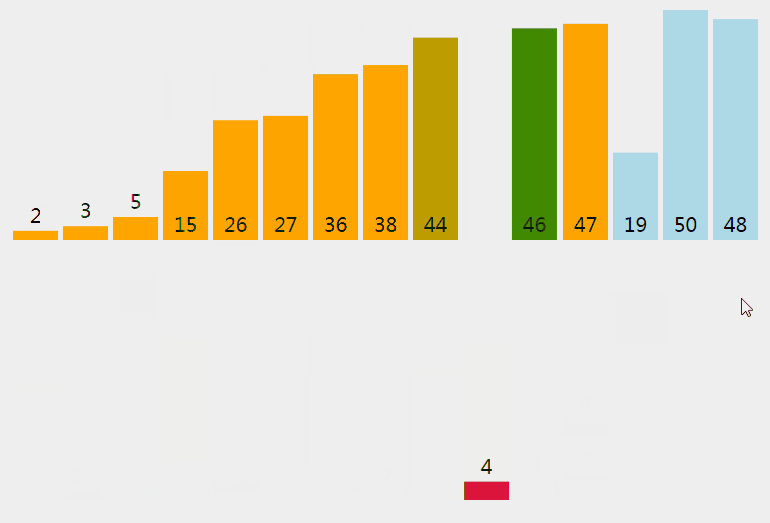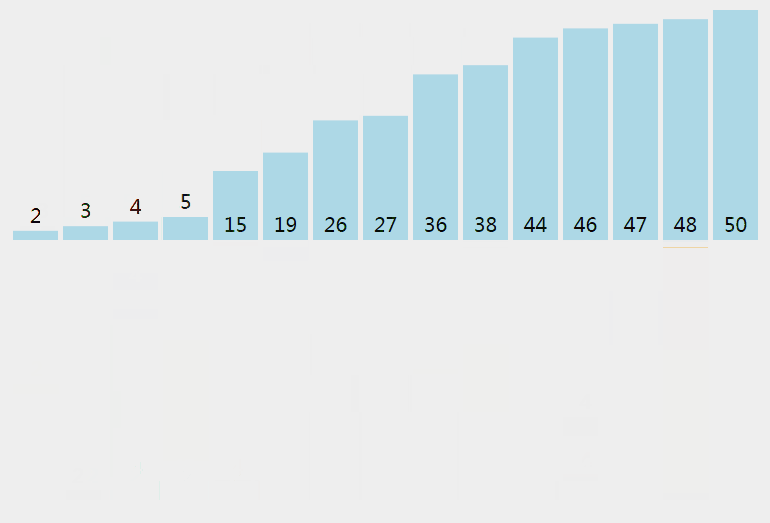
顺序从数组里取出数据,然后插入到前面有序数组里
private int[] Insertion(int[] list) //插入排序 传入数组 3, 6, 2, 1, 9, 5, 4, 7 { for (int i = 1; i < list.Length; i++) //首选取出第一个数(3)作为一个有序的数组,然后遍历传入数组"3"之后的每一个数 { int j; int key = list[i]; for (j = i - 1; j >= 0; j--) //因为取出来的数是一个有序数组,排序是从小往大递增的,所以插入新的数字的时候只需要 { if (list[j] < key) //==>倒序比较,假如比数组的最后一个数字大,前面的就不需要再比较了,这里就是最先比较的 { break; //最大数就是list[j] } else { list[j + 1] = list[j]; //假如待插入数字不比最大的一个数字大,就依次跟前面的数字比较,同时把比较过的数字 } //位置依次右移 } list[j + 1] = key; //最后找到合适的位置插入数组 } return list; }
5.希尔排序

对i跟i+gap比较,直至gap==1,比较完成
public static void ShellSort(int[] array) { int gap = array.Length / 2; while (1 <= gap) { // 把距离为 gap 的元素编为一个组,扫描所有组 for (int i = gap; i < array.Length; i++) { int j = 0; int temp = array[i]; // 对距离为 gap 的元素组进行排序 for (j = i - gap; j >= 0 && temp < array[j]; j = j - gap) { array[j + gap] = array[j]; } array[j + gap] = temp; } gap = gap / 2; // 减小增量 } }
6.归并排序
将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个有序的子序列,再把有序的子序列合并为整体有序序列。归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法。
public static void MergeSort(int[] inputAray, int first, int end) { if (first < end) { int midIndex = (first + end) / 2; MergeSort(inputAray, first, midIndex); MergeSort(inputAray, midIndex + 1, end); MergeMethid(inputAray, first, midIndex, end); } } private static void MergeMethid(int[] inputAray, int first, int midIndex, int end) { int[] temp = new int[end - first + 1]; int m = first; int n = midIndex + 1; int k = 0; while (m <= midIndex && n < end) { if (inputAray[m] < inputAray[n]) { temp[k] = inputAray[m]; k++; m++; } else { temp[k] = inputAray[n]; k++; n++; } } while (m <= midIndex) { temp[k] = inputAray[m]; k++; m++; } while (n < end) { temp[k] = inputAray[n]; k++; n++; } for (k=0,m = first; m < end; k++,m++) { inputAray[m] = temp[k]; } }
7.堆排序
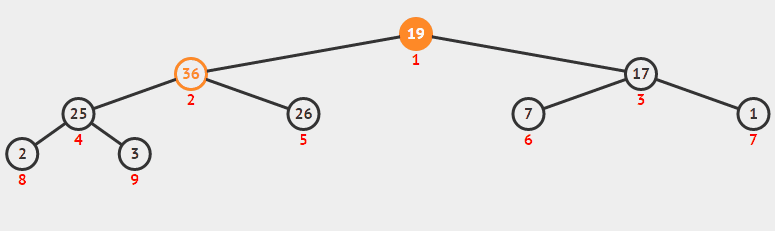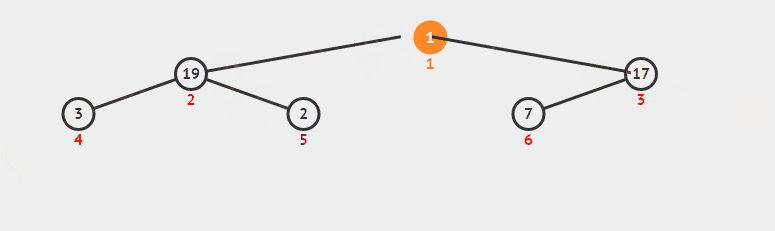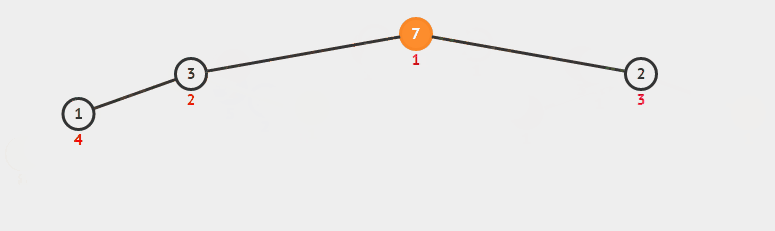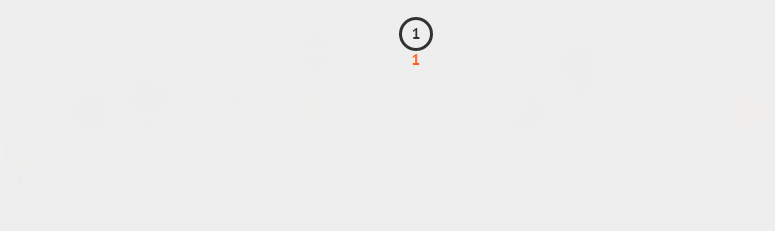
public static IList<int> HeapSort(int maxIdx, int[] lst) { int i = lst.Length - 1; int k = 0; while (i > -1) { Swap(maxIdx, i, lst); k++; //每次缩短无序区最大位置 maxIdx = GetMax(lst.Length - k, lst); i--; } return lst; } public static void Swap(int maxIdx, int idx, int[] lst) { int midx = maxIdx; int temp = lst[idx]; lst[idx] = lst[maxIdx]; lst[maxIdx] = temp; } public static int GetMax(int maxLen, int[] lst) { int maxIdx = 0; for (var i = 0; i < maxLen; i++) { if (lst[i] > lst[maxIdx]) maxIdx = i; } return maxIdx; }
8.定时器的实现
update
public float timer = 1.0f; // 定时2秒
void Update() {
timer -= Time.deltaTime;
if (timer <= 0) {
doSomething();
timer = 2.0f;
}
}
monobehavie.invoke
协程
9.二分查找
int binarySearch(int[] nums, int target) { int left = 0; int right = nums.length - 1; // 注意 while(left <= right) { // 注意 int mid = (right + left) / 2; if(nums[mid] == target) return mid; else if (nums[mid] < target) left = mid + 1; // 注意 else if (nums[mid] > target) right = mid - 1; // 注意 } return -1; }
10.遍历二叉树
// 二叉树前序遍历 根-> 左-> 右 public static void preOrderTraveral(TreeNode node) { if(node == null) { return; } System.out.print(node.data+" "); preOrderTraveral(node.leftChild); preOrderTraveral(node.rightChild); }
//二叉树中序遍历 左-> 根-> 右 public static void inOrderTraveral(TreeNode node) { if (node == null) { return; } inOrderTraveral(node.leftChild); System.out.print(node.data + " "); inOrderTraveral(node.rightChild); }
// 二叉树后序遍历 左-> 右-> 根 public static void postOrderTraveral(TreeNode node) { if (node == null) { return; } postOrderTraveral(node.leftChild); postOrderTraveral(node.rightChild); System.out.print(node.data + " "); }
public static void levelOrder(TreeNode root) { LinkedList<TreeNode> queue = new LinkedList<>(); queue.add(root); while (!queue.isEmpty()) { root = queue.pop(); System.out.print(root.data + " "); if (root.leftChild != null) queue.add(root.leftChild); if (root.rightChild != null) queue.add(root.rightChild); } }
11.Dijkstra最短路径算法
//V1到V7的邻接矩阵 static int[,] Metro = new int[7, 7] { { 0, 3, 7, 5,2048,2048,2048}, { 3, 0, 2,2048, 6,2048,2048}, { 7, 2, 0, 3, 3,2048,2048}, { 5,2048, 3, 0,2048, 2, 8}, {2048, 6, 3,2048, 0,2048, 2}, {2048,2048,2048, 2,2048, 0, 2}, {2048,2048,2048, 8, 2, 2, 0}}; static int row = 7; ArrayList S = new ArrayList(row);//S储存确定最短路径的顶点的下标 ArrayList U = new ArrayList(row);//U中存储尚未确定路径的顶点的下标 int[] distance = new int[7];//用以每次查询存放数据 int[] prev = new int[7];//用以存储前一个最近顶点的下标 bool[] Isfor = new bool[7] { false, false, false, false, false, false, false }; /// <summary> /// dijkstra算法的实现部分 /// </summary> /// <param name="Start"></param> void FindWay(int Start) { S.Add(Start); Isfor[Start] = true; for (int i = 0; i < row; i++) { if (i != Start) U.Add(i); } for (int i = 0; i < row; i++) { distance[i] = Metro[Start, i]; prev[i] = 0; } int Count = U.Count; while (Count > 0) { int min_index = (int)U[0];//假设U中第一个数存储的是最小的数的下标 foreach (int r in U) { if (distance[r] < distance[min_index] && !Isfor[r]) min_index = r; } S.Add(min_index);//S加入这个最近的点 Isfor[min_index] = true; U.Remove(min_index);//U中移除这个点; foreach (int r in U) { //查找下一行邻接矩阵,如何距离和上一个起点的距离和与数组存储的相比比较小,就更改新的距离和起始点,再比对新的起点到各边的距离 if (distance[r] > distance[min_index] + Metro[min_index, r]) { distance[r] = distance[min_index] + Metro[min_index, r]; prev[r] = min_index; } else { distance[r] = distance[r]; } } Count = U.Count; } }
6. 手撕代码,字符串单词反转
1、手撕最小子矩阵。
3、场景题:实现空投点如何在一个圆内均匀且随机。
比如:一个数组,怎么不用循环,不逐一赋值,把它逆序输出。
6. 二维数组, 左上角到右下角 走过的点和最小多少( 矩阵dp)
7. 判断点在三角形
-- 问了下碰撞检测四叉树
2. 手撕十进制反转 123->321 (一开始以为01反转直接返回了 ~num, 面试官:?)
3. 手撕字符串去掉空格,要求用char* 操作( 开了新字符串,实际上可以记空格数遍历时去除,而且面试官说有语法问题)
4. 手撕数组内k高频数据 (先统计频率 map/桶; 然后用小顶堆维护其中k大的频率 复杂度nlogk)
12. 手撕 双链表反转
2. 游戏内如何判断一个点在空气墙内?(空气墙一般是AABB。 若问是否可达可以用射线判断)
3. 如何判断一个点在多边形内 ? 如何判断一个点在三角形内
6. 快速求中位数
两个堆栈实现队列操作
1.缓存算法


 浙公网安备 33010602011771号
浙公网安备 33010602011771号