YBTOJ 梳理总结
包简洁的
1. 基础算法
顾名思义,基础算法就是其他算法的基础。例如,递推算法是 DP 的基础,贪心算法是堆的应用的基础,DFS 是图论的基础。所以说,许多算法都是在这些算法的基础上进行其他操作的。所以说学习好这些算法尤为重要。
技巧总结:
1-A 将一维的信息转化为二维。
1-B 从 A 到 B 统计较困难,可以从 B 到 A 统计。
1-C 按照右端点排序,进行贪心。
1-D 二进制拆分,按位处理。
1-E 遇到“最大值最小”考虑二分。
1-F 建立正图和反图可以判断从起点到终点的路径中某个点是否被经过。
1-G 对称的操作可以只计算一边。
知识点:
(过于简单的知识点不予显示)
1-1 卡特兰数
1-2 斐波那契数列
1-3 堆
1-4 STL的应用
1-5 哈夫曼树
1-6 实数域上的二分
1-7 折半搜索
1-8 启发式迭代加深搜索(IDA*)
1-9 洪水填充
1.0 模板讲解
好像没啥模板,哈夫曼树不太会,先咕一下。
1.1 递推算法
G. 无限序列
对应知识点 1-2
找规律,发现序列与斐波那契序列有关。也就是,这个序列是由上一个序列和上上个序列拼接而成的。那么 \(1\) 的个数和 \(0\) 的个数也满足斐波那契序列的规律。这样问题就迎刃而解了。
H. 序列个数
对应技巧 1-A
非常巧妙的一道题。
我们考虑一个矩阵 \(A\),有 \(A_{i, b_i} = 1\),其余位置为 \(0\)。那么我们左上角为 \((1, 1)\) 右下角为 \((i, i)\) 的子矩阵内,\(1\) 的个数为 \(a_i\)。这样就可以比较方便地进行递推转移了。
1.2 贪心算法
B. 雷达装置
对应技巧 1-B、1-C
注意到雷达在 \(x\) 轴上,是一维的,而建筑物的点是二维的。也就是说,我们直接考虑雷达覆盖建筑物维度较高,实现较难。不如这样考虑:我们一个建筑物,要想被雷达覆盖,那么就以它为圆心画一个圆(包含内部),那么必须有雷达在这个圆内。但是,雷达只能在 \(x\) 轴上,所以雷达一定在这个圆与 \(x\) 轴相交的一条线段上。其实这就是一个区间。
所以说问题转化为:一堆区间,选定最少的点,使得每个区间内都至少一定有一个点。
贪心策略:先按右端点排序,从小往大扫。然后如果发现了一个区间没被覆盖,那就在这个区间右边放一个新雷达。
如何证明?显然,这几个雷达代表的区间没有交集。所以这种方法一定是最优的。这种贪心策略很经典,应用很广泛。务必要掌握。
1.3 二分算法
都是基础题,没啥好讲的。
1.4 深度搜索
F. 骑士精神
对应知识点 1-8
迭代加深:给搜索树做个限高,像本题中“最大不超过 \(15\) 步”。
启发式搜索:带估价函数,\(f(x) = g(x) + h(x)\),\(f(x)\) 为 \(x\) 的估价函数,\(g(x)\) 为当前步数,\(h(x)\) 是对未来步数的最完美估计。
综合这两个就行了。
1.5 广度搜索
码就完了,没啥技术含量。
2. 字符串算法
好戏才刚刚开始...
这章都是字符串的题,当然,还有哈希。
技巧总结:
2-A 字符串的最段循环节长度为 \(n - nxt_n\),如果有解的话。\(nxt_n\) 表示字符串的最长公共前后缀长度。
2-B 与二进制有关的问题可以考虑 01-Trie,其实这结合了 1-D。
知识点:
2-1 字符串哈希
2-2 哈希
2-3 Manacher(不一定要掌握)
2-4 字典树
2-5 AC自动机
2.0 模板讲解
A. KMP
注意到 \(nxt\) 值为最长公共前后缀的长度,所以我们只需要匹配时不断跳 \(nxt\)。
解释:失配情况在于文本串的后缀与模式串的后缀不匹配,这时候需要移动模式串的 \(j\) 指针,跳到 \(nxt\),即 \(j = nxt_j\),这样文本串的后缀与模式串的前缀匹配,文本串指针不用移动,大大降低了复杂度。
图解:
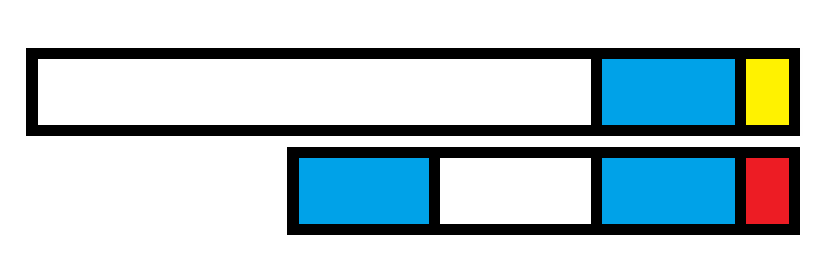
其中,蓝色部分为最长公共前后缀。黄色、红色部分为失配点。这时候,它会变成:
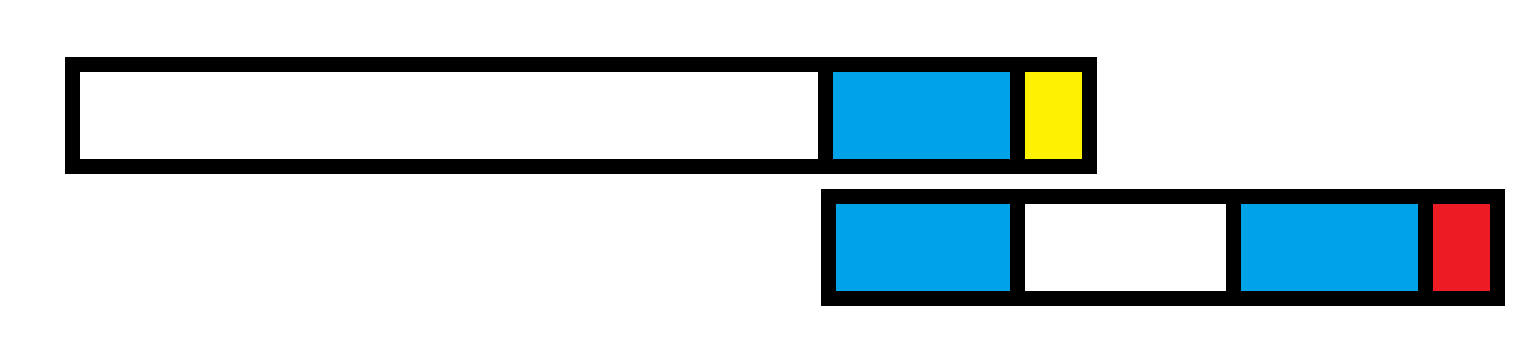
这就是 KMP 的操作。
\(nxt\) 数组的求法相当于一个 DP 的过程,也可以理解为“自己匹配自己”。其实与上面几乎一样,无非就是用已知的 \(nxt\) 值去推未知的。
代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 2e6 + 10;
char a[N], b[N];
int la, lb, nxt[N];
int main() {
cin >> a >> b;
la = strlen(a), lb = strlen(b);
nxt[0] = nxt[1] = 0;
int j = 0;
for (int i = 1; i < lb; i++) {
while (j && b[i] != b[j]) j = nxt[j];
if (b[i] != b[j]) nxt[i + 1] = 0;
else nxt[i + 1] = ++j;
}
j = 0;
for (int i = 0; i < la; i++) {
while (j && a[i] != b[j]) j = nxt[j];
if (a[i] == b[j]) j++;
if (j == lb) printf("%d\n", i - lb + 2);
}
for (int i = 1; i <= lb; i++) {
printf("%d ", nxt[i]);
}
return 0;
}
B. 字典树
没啥好讲的,没有节点就新建一个即可。
代码:
void insert(string s) {
int u = 0;
for (int i = 0; i < s.size(); i++) {
int x = s[i] - 'a';
if (!tr[u][x]) tr[u][x] = ++tot;
u = tr[u][x];
}
cnt[u]++;
}
C. AC自动机


