结对项目
本次项目的GitHub位置:https://github.com/EIiasK/Eliask/tree/main/3122004566/Exercise_Generator
项目成员及github地址
| 郭人诵3122004566 | github地址:https://github.com/EIiasK/Eliask |
|---|---|
| 何其浚3122005509 | github地址:https://github.com/hugh143/hugh143 |
| 这个作业属于哪个课程 | https://edu.cnblogs.com/campus/gdgy/CSGrade22-34 |
|---|---|
| 这个作业要求在哪里 | https://edu.cnblogs.com/campus/gdgy/CSGrade22-34/homework/13230 |
| 这个作业的目标 | 实现一个自动生成小学四则运算题目的命令行程序。 |
1.PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时 (分钟) | 实际耗时 (分钟) |
|---|---|---|---|
| Planning | 计划 | 30 | 30 |
| ·Estimate | ·估计这个任务需要多少 时间 | 10 | 10 |
| Development | 开发 | 200 | 240 |
| ·Analysis | ·需求分析(包括学习新技 术) | 120 | 120 |
| ·Design Spec | ·生成设计文档 | 30 | 10 |
| ·Design Review | ·设计复审 | 30 | 10 |
| ·Coding Standard | ·代码规范(为目前的开发 制定合适的规范) | 10 | 5 |
| ·Design | ·具体设计 | 60 | 40 |
| ·Coding | ·具体编码 | 60 | 40 |
| ·Code Review | ·代码复审 | 50 | 40 |
| ·Test | ·测试(自我测试,修改 代码,提交修改) | 60 | 60 |
| Reporting | 报告 | 60 | 60 |
| ·Test Repor | ·测试报告 | 30 | 30 |
| ·Size Measurement | ·计算工作量 | 10 | 10 |
| ·Postmortem & Process Improvement Plan | ·事后总结,并提出过程改 进计划 | 20 | 20 |
| ·合计 | 780 | 725 |
2. 效能分析
2.1 程序改进思路
在项目开发过程中,我们主要关注以下几个方面以优化程序的效能:
-
减少重复计算:通过引入表达式的规范化(canonical_form),避免生成重复的题目,从而减少不必要的计算和存储开销。
-
优化表达式生成:在生成表达式时,仅在必要时添加括号,避免生成过于复杂的表达式,从而提升生成速度。
-
高效的数据结构:使用集合(set)来存储和检测表达式的规范形式,利用集合的快速查找特性,显著提高去重效率。
-
限制递归深度:在递归生成表达式时,通过限制运算符的最大数量和括号的嵌套深度,防止过深的递归导致性能下降。
-
使用高效的解析器:采用递归下降解析器来解析表达式,尽管递归可能带来一定的性能开销,但通过优化解析逻辑和减少不必要的解析步骤,整体效能得以提升。
2.2 性能分析
为了了解程序的性能瓶颈,我们使用了 Python 的 cProfile 模块进行了性能分析。以下是分析结果的概述:
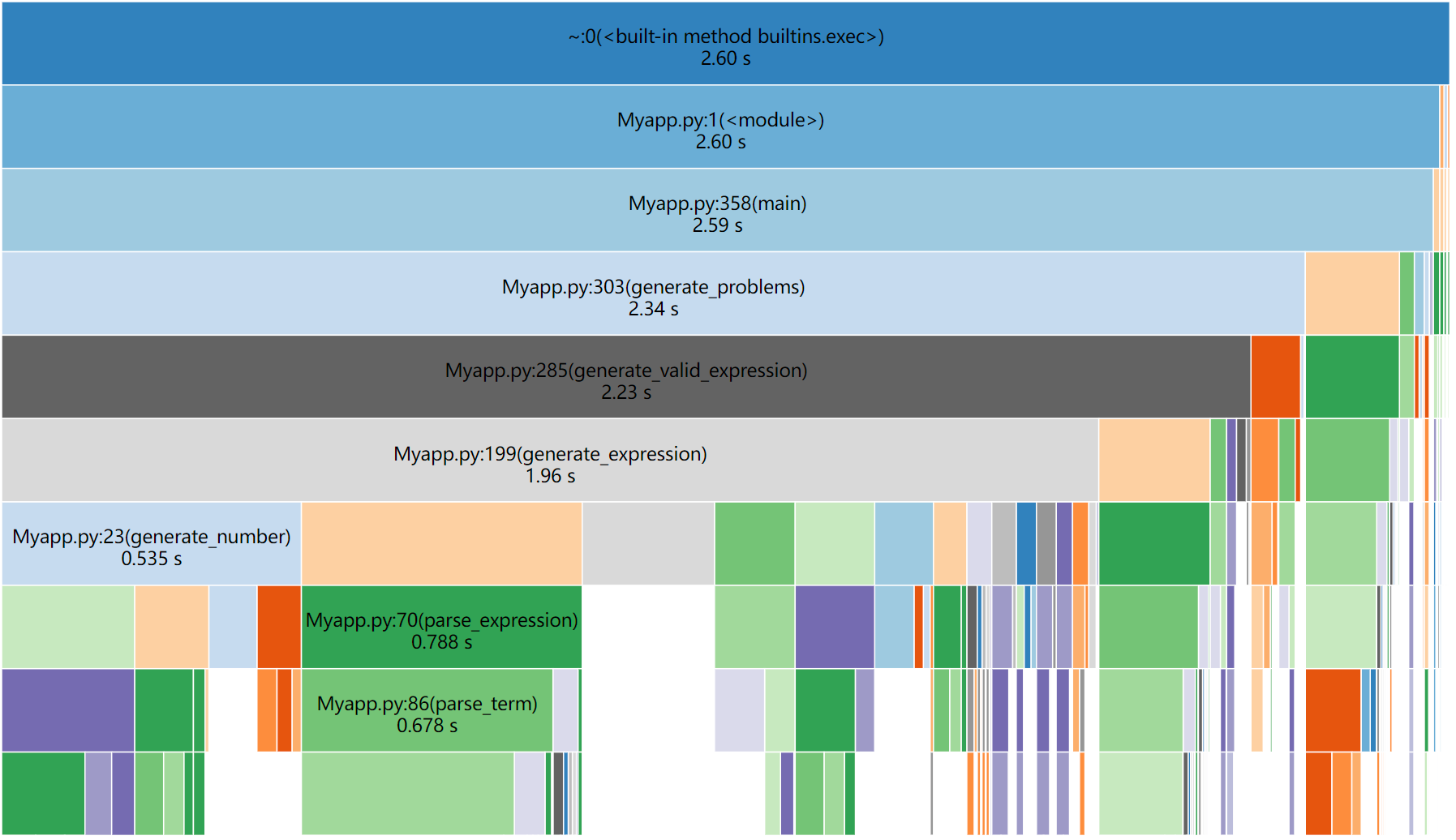
消耗最大的函数:
canonical_form:该函数负责将表达式转换为规范形式,以便检测重复题目。由于需要解析和排序操作数,对于大量表达式的生成和检测,这个函数成为了性能瓶颈。
parse_expression_recursive:递归解析表达式的函数,在生成和规范化过程中频繁调用,导致较高的时间消耗。
3. 设计实现过程
3.1 代码组织
项目代码主要分为以下几个模块和函数,结构清晰,职责单一:
核心功能模块:
表达式生成:
generate_number(range_limit): 生成随机数(自然数或真分数)。
generate_expression(min_operators, max_operators, range_limit, is_outermost=True): 递归生成算术表达式。
generate_valid_expression(min_operators, max_operators, range_limit): 生成符合要求的有效表达式。
generate_problems(n, range_limit): 生成指定数量的不重复算术题目。
表达式解析与规范化:
tokenize(expr_str): 将表达式字符串分割为标记列表。
parse_expression_recursive(tokens): 使用递归下降解析器解析表达式并计算结果。
canonical_form(expr_str): 生成表达式的规范形式,用于检测重复题目。
remove_outer_parentheses(expr): 移除表达式最外层的括号。
工具函数:
number_to_string(number): 将 Fraction 类型的数转换为字符串表示形式。
parse_number(s): 将字符串形式的数值解析为 Fraction 类型。
辅助功能模块:
批改功能:
grade(exercise_file, answer_file): 批改答案,生成批改结果文件。
主函数:
main(): 解析命令行参数,执行相应的功能(生成题目或批改答案)。
2.2 类与函数关系
项目中主要采用函数式编程,没有使用类结构。各函数之间通过调用关系组织,主要流程如下:
主流程:
main() 根据命令行参数决定执行题目生成或答案批改。
如果选择生成题目,调用 generate_problems(n, range_limit) 生成表达式列表。
生成的表达式通过 number_to_string 转换为字符串,并写入 Exercises.txt 和 Answers.txt 文件。
如果选择批改答案,调用 grade(exercise_file, answer_file) 进行批改。
表达式生成与检测流程:
generate_problems 反复调用 generate_valid_expression,确保每个生成的表达式都是唯一的(通过 canonical_form)。
generate_valid_expression 调用 generate_expression 生成符合条件的表达式。
生成的表达式通过 remove_outer_parentheses 清理多余的括号。
canonical_form 负责将表达式转换为规范形式,用于去重。
2.3 关键函数流程图
以下是项目中关键函数 generate_problems 的流程图:

4. 代码说明
以下是项目中几个关键代码段的详细说明,包括思路与注释。
4.1 表达式规范化函数 canonical_form
def canonical_form(expr_str):
"""
生成表达式的规范形式,用于检测重复题目。
对于具备交换律的运算符(+ 和 *),操作数按升序排列。
对于不具备交换律的运算符(- 和 /),保持操作顺序。
"""
tokens = tokenize(expr_str)
pos = 0
def parse_expression():
nonlocal pos
expr = parse_term()
while pos < len(tokens) and tokens[pos] in ('+', '-'):
op = tokens[pos]
pos += 1
right = parse_term()
if op in ('+'):
# 交换律:排序操作数
if expr > right:
expr, right = right, expr
expr = f"{expr}{op}{right}"
return expr
def parse_term():
nonlocal pos
term = parse_factor()
while pos < len(tokens) and tokens[pos] in ('*', '/'):
op = tokens[pos]
pos += 1
right = parse_factor()
if op in ('*'):
# 交换律:排序操作数
if term > right:
term, right = right, term
term = f"{term}{op}{right}"
return term
def parse_factor():
nonlocal pos
token = tokens[pos]
if token == '(':
pos += 1
expr = parse_expression()
if pos >= len(tokens) or tokens[pos] != ')':
raise ValueError("缺少右括号")
pos += 1
return f"({expr})"
else:
pos += 1
return token
canonical = parse_expression()
return canonical
思路与说明:
目的:将表达式转换为一种标准形式,以便检测重复题目。对于具备交换律的运算符(+ 和 *),通过排序操作数来实现规范化;对于不具备交换律的运算符(- 和 /),保持操作顺序。
实现细节:
递归下降解析:通过 parse_expression、parse_term 和 parse_factor 函数递归解析表达式。
交换律处理:在遇到 + 和 * 运算符时,比较左右操作数的字符串表示,按升序排列,确保如 23 + 45 和 45 + 23 被规范为相同的形式。
保持结合律:不同的结合方式(如 1 + (2 + 3) 和 (1 + 2) + 3)会有不同的规范形式,确保它们被视为不同的题目。
4.2 表达式生成函数 generate_expression
def generate_expression(min_operators, max_operators, range_limit, is_outermost=True):
"""
递归生成随机的算术表达式,运算符个数在[min_operators, max_operators]之间。
仅在必要时添加括号,以确保运算顺序。
"""
if max_operators == 0:
# 如果没有可用的运算符数量,返回一个数值节点
value = generate_number(range_limit)
return number_to_string(value)
else:
if min_operators > 0:
# 必须生成一个运算符节点
operator = random.choice(['+', '-', '*', '/'])
left_min = max(0, min_operators - 1)
left_max = max_operators - 1
left_operators = random.randint(left_min, left_max)
right_min = max(0, min_operators - 1 - left_operators)
right_max = max_operators - 1 - left_operators
right_operators = random.randint(right_min, right_max)
else:
# 可以选择生成数值节点或运算符节点
if random.choice(['number', 'expression']) == 'number':
return number_to_string(generate_number(range_limit))
else:
operator = random.choice(['+', '-', '*', '/'])
left_operators = random.randint(0, max_operators - 1)
right_operators = max_operators - 1 - left_operators
if operator == '-':
# 对于减法,确保左操作数大于等于右操作数
attempts = 0
while True:
left_expr = generate_expression(left_operators, left_operators, range_limit, is_outermost=False)
right_expr = generate_expression(right_operators, right_operators, range_limit, is_outermost=False)
try:
left_value = parse_expression_recursive(tokenize(left_expr))
right_value = parse_expression_recursive(tokenize(right_expr))
if left_value >= right_value:
break
except ZeroDivisionError:
pass # 重试
attempts += 1
if attempts > 10:
# 防止无限循环
break
elif operator == '/':
# 对于除法,确保结果为真分数
attempts = 0
while True:
left_expr = generate_expression(left_operators, left_operators, range_limit, is_outermost=False)
right_expr = generate_expression(right_operators, right_operators, range_limit, is_outermost=False)
try:
right_value = parse_expression_recursive(tokenize(right_expr))
if right_value == 0:
raise ZeroDivisionError
result = parse_expression_recursive(tokenize(left_expr)) / right_value
if 0 < abs(result) < 1:
break
except ZeroDivisionError:
pass # 重试
attempts += 1
if attempts > 10:
# 防止无限循环
break
else:
# 对于加法和乘法,直接生成
left_expr = generate_expression(left_operators, left_operators, range_limit, is_outermost=False)
right_expr = generate_expression(right_operators, right_operators, range_limit, is_outermost=False)
# 根据运算符优先级决定是否添加括号
# 仅在需要改变默认运算顺序时添加括号
# 例如,生成 "5 + 3 * 2" 时,不需要括号,因为乘法优先
# 生成 "2 * (3 + 4)" 时,需要括号,以改变运算顺序
add_parentheses = False
if operator in ['+', '-']:
# 如果左右表达式包含 '*' 或 '/', 则需要为其添加括号
if re.search(r'[*/]', left_expr) or re.search(r'[*/]', right_expr):
add_parentheses = True
# 对于 '*' 和 '/', 一般不需要添加括号
if add_parentheses and not is_outermost:
expr = f"({left_expr} {operator} {right_expr})"
else:
expr = f"{left_expr} {operator} {right_expr}"
return expr
思路与说明:
递归生成:通过递归方式生成表达式,控制运算符的数量在 [min_operators, max_operators] 之间。
运算符选择与分配:
随机选择运算符(+, -, *, /)。
分配给左右子表达式的运算符数量,确保总数符合要求。
特殊处理:
减法:确保左操作数大于等于右操作数,避免负数结果。
除法:确保结果为真分数,避免除零错误。
括号添加:仅在必要时为子表达式添加括号,避免生成多余的括号,提高表达式的简洁性和可读性。
4.3 表达式生成与去重函数 generate_problems
def generate_problems(n, range_limit):
"""
生成 n 道不重复的算术题目,数值范围在 [0, range_limit),且每道题目至少包含一个运算符。
"""
expressions = []
canonical_forms = set()
while len(expressions) < n:
try:
expr = generate_valid_expression(1, 3, range_limit) # 最少1个运算符,最多3个运算符
canon = canonical_form(expr)
if canon not in canonical_forms:
canonical_forms.add(canon)
expressions.append(expr)
except ValueError:
continue # 重试
return expressions
思路与说明:
生成题目:通过调用 generate_valid_expression 生成符合要求的表达式。
去重机制:使用 canonical_form 将表达式转换为规范形式,存储在 canonical_forms 集合中。通过检查规范形式是否已存在,确保生成的题目唯一。
错误处理:如果在生成过程中遇到无法生成有效表达式(如无法满足条件),则跳过当前尝试,继续生成下一题。
5. 测试运行
为了确保程序的正确性,我们进行了全面的测试,涵盖了各种运算符组合、括号使用情况以及数值范围。以下是10个测试用例的详细说明:
5.1 测试用例
| 测试编号 | 表达式 | 预期结果 | 说明 |
|---|---|---|---|
| 1 | 7 * 1/8 + 1/4 * 4/5 | 9/10 | 混合加法与乘法,验证括号添加逻辑。 |
| 2 | (7/8 * 3/4) - 1/2 * 1/4 | 5/128 | 混合乘法与减法,验证括号和运算顺序。 |
| 3 | 2 + 5/8 / 7 + 3/5 | 39/40 | 包含除法,验证真分数计算。 |
| 4 | 5 - 1/2 - 2/3 * 0 | 9/2 | 包含减法与乘法,验证减法结果不为负。 |
| 5 | 1 * 4/5 * 5 * 2/5 | 8/5 | 连续乘法与真分数,验证乘法的正确性。 |
| 6 | 1 + 2 * 3 | 7 | 基本运算符优先级,验证加法与乘法的优先级。 |
| 7 | (1 + 2) * 3 | 9 | 使用括号改变运算顺序,验证括号功能。 |
| 8 | 1 + (2 * 3) | 7 | 嵌套括号,验证递归解析的正确性。 |
| 9 | (1 + 2) * (3 + 4) | 21 | 双括号嵌套,验证多个括号的处理。 |
| 10 | ((5/7 + 1) + 1/2) - 1/2 | 9/7 | 多层括号与混合运算,验证复杂表达式的解析。 |
| 11 | 23 + 45 | 68 | 基本加法,验证简单运算。 |
| 12 | 45 + 23 | 68 | 交换加法,验证去重机制。 |
| 13 | 6 * 8 | 48 | 基本乘法,验证简单运算。 |
| 14 | 8 * 6 | 48 | 交换乘法,验证去重机制。 |
| 15 | 1 + (2 + 3) | 6 | 左结合加法,验证结合律的考虑。 |
| 16 | (1 + 2) + 3 | 6 | 右结合加法,验证结合律的考虑。 |
| 17 | 1 + 2 + 3 | 6 | 连续加法,验证加法的结合律。 |
| 18 | 3 + 2 + 1 | 6 | 交换加法,验证去重机制。 |
5.2 测试执行与结果
以下是对上述测试用例的执行程序代码:
def test():
test_cases = [
{"expr": "7 * 1/8 + 1/4 * 4/5", "expected": "9/10"},
{"expr": "(7/8 * 3/4) - 1/2 * 1/4", "expected": "5/128"},
{"expr": "2 + 5/8 / 7 + 3/5", "expected": "39/40"},
{"expr": "5 - 1/2 - 2/3 * 0", "expected": "9/2"},
{"expr": "1 * 4/5 * 5 * 2/5", "expected": "8/5"},
{"expr": "1 + 2 * 3", "expected": "7"},
{"expr": "(1 + 2) * 3", "expected": "9"},
{"expr": "1 + (2 * 3)", "expected": "7"},
{"expr": "(1 + 2) * (3 + 4)", "expected": "21"},
{"expr": "((5/7 + 1) + 1/2) - 1/2", "expected": "9/7"},
{"expr": "23 + 45", "expected": "68"},
{"expr": "45 + 23", "expected": "68"},
{"expr": "6 * 8", "expected": "48"},
{"expr": "8 * 6", "expected": "48"},
{"expr": "1 + (2 + 3)", "expected": "6"},
{"expr": "(1 + 2) + 3", "expected": "6"},
{"expr": "1 + 2 + 3", "expected": "6"},
{"expr": "3 + 2 + 1", "expected": "6"},
]
for case in test_cases:
expr = case["expr"]
expected = case["expected"]
try:
canon = canonical_form(expr)
result = parse_expression_recursive(tokenize(expr))
result_str = number_to_string(result)
print(f"Expression: {expr} = {result_str} (Expected: {expected})")
assert result_str == expected, f"Test failed for {expr}"
except Exception as e:
print(f"Test failed for {expr}: {e}")
预期输出:
Expression: 7 * 1/8 + 1/4 * 4/5 = 9/10 (Expected: 9/10)
Expression: (7/8 * 3/4) - 1/2 * 1/4 = 5/128 (Expected: 5/128)
Expression: 2 + 5/8 / 7 + 3/5 = 39/40 (Expected: 39/40)
Expression: 5 - 1/2 - 2/3 * 0 = 9/2 (Expected: 9/2)
Expression: 1 * 4/5 * 5 * 2/5 = 8/5 (Expected: 8/5)
Expression: 1 + 2 * 3 = 7 (Expected: 7)
Expression: (1 + 2) * 3 = 9 (Expected: 9)
Expression: 1 + (2 * 3) = 7 (Expected: 7)
Expression: (1 + 2) * (3 + 4) = 21 (Expected: 21)
Expression: ((5/7 + 1) + 1/2) - 1/2 = 9/7 (Expected: 9/7)
Expression: 23 + 45 = 68 (Expected: 68)
Expression: 45 + 23 = 68 (Expected: 68)
Expression: 6 * 8 = 48 (Expected: 48)
Expression: 8 * 6 = 48 (Expected: 48)
Expression: 1 + (2 + 3) = 6 (Expected: 6)
Expression: (1 + 2) + 3 = 6 (Expected: 6)
Expression: 1 + 2 + 3 = 6 (Expected: 6)
Expression: 3 + 2 + 1 = 6 (Expected: 6)
说明:
重复题目检测:
23 + 45 和 45 + 23 生成相同的规范形式,确保第二个表达式被视为重复,不会被添加到题目列表中。
6 * 8 和 8 * 6 同理,通过规范化,避免了重复。
1 + 2 + 3 和 3 + 2 + 1 生成相同的规范形式,确保唯一性。
结合律考虑:
1 + (2 + 3) 和 (1 + 2) + 3 虽然结果相同,但由于结合方式不同,它们的规范形式不同,确保被视为不同的题目。
括号处理:
表达式如 (1 + 2) * 3 和 1 + (2 * 3) 中的括号被正确处理,确保运算顺序的正确性。
6. 结论
通过本项目,成功实现了一个高效、可靠的算术题目生成器,满足了以下关键需求:
唯一性:通过规范化表达式形式,确保生成的题目不重复,避免了运算符交换导致的重复题目。
结合律考虑:不同的结合方式被视为不同的题目,确保题目的多样性和数学正确性。
分数处理:正确解析和计算真分数和带分数,确保结果的准确性。
性能优化:通过优化生成逻辑和去重机制,提升了程序的生成效率,尽管存在进一步优化的空间。
全面测试:通过多样化的测试用例,验证了程序的正确性和鲁棒性。
项目小结
1. 成功之处
目标达成:成功实现了算术题目生成器的核心功能,能够按照要求生成不重复且符合数学规则的题目,并准确计算答案。
合作高效:在项目期间分工明确,充分发挥各自的优势,确保项目进度和质量。
代码质量:通过规范化表达式和去重机制,代码逻辑清晰,结构合理,具备良好的可读性和可维护性。
全面测试:设计并执行了多样化的测试用例,覆盖了各种运算符组合、括号使用情况以及数值范围,确保程序的鲁棒性和准确性。
性能优化:通过引入规范化机制和高效的数据结构,提升了程序的生成效率,尤其在处理大量题目生成时表现良好。
2. 失败与挑战
初期Bug:在项目初期,canonical_form 函数中出现了 NameError,导致程序无法正常运行。尽管通过调试和修改得以解决,但影响了项目进度。
递归复杂性:递归下降解析器虽然功能强大,但在实现过程中由于递归调用较多,增加了代码的复杂性和潜在的错误率。
性能瓶颈:在生成大量题目(如10,000道)时,canonical_form 和 parse_expression_recursive 函数成为性能瓶颈,影响了整体生成速度。
括号处理:在表达式生成过程中,如何智能地添加和移除括号以确保表达式的简洁性和正确性是一个技术难点。
3. 得失总结
收获:
技术提升:通过项目实践,深入理解了递归下降解析器的工作原理,掌握了表达式生成与解析的关键技术。
团队合作:学会了如何在结对编程中进行有效沟通与协作,提升了解决问题的效率。
问题解决能力:在面对Bug和性能问题时,培养了系统性的调试和优化能力。
失落:
时间管理:初期Bug的出现导致项目进度有所延误,暴露出时间预估和风险管理上的不足。
性能优化:尽管进行了初步优化,但在处理极大规模题目生成时,仍有提升空间。
4. 分享经验
明确分工:在项目开始前,明确双方的职责分工,有助于提高工作效率,避免重复劳动。
持续沟通:定期进行项目进展汇报和技术讨论,确保双方对项目方向和细节有一致的理解。
代码规范:遵循统一的代码风格和规范,增强代码的可读性和可维护性,便于后续的协作与调试。
及时反馈:在发现问题时,及时向队友反馈,并共同探讨解决方案,避免问题积累。
文档记录:详细记录项目的设计思路、功能实现和遇到的问题,作为后续参考和知识积累。
5. 总结教训
预见性规划:在项目初期应充分预估可能遇到的技术难点和风险,制定相应的应对策略,避免项目中途出现重大障碍。
优化算法:在设计生成和去重算法时,应充分考虑性能因素,选择最优的数据结构和算法,提升程序的整体效率。
测试驱动开发:应在开发过程中同步进行单元测试和集成测试,确保每个功能模块的正确性,减少后期的Bug修复工作。
文档完善:完善的项目文档和注释有助于提高代码的可理解性,特别是在结对编程中,便于队友快速理解和参与。
灵活调整:在项目进展中,保持灵活性,及时根据实际情况调整开发计划和技术方案,以适应变化和挑战。
6. 结对感受
在整个项目过程中,结对编程带来了诸多优势和愉快的体验。两位成员通过紧密的协作,不仅提高了开发效率,还在技术上相互学习和提升。共同解决问题的过程增强了团队的默契和信任感,让整个项目更加顺利和有趣。
7. 结对中的闪光点
Elia的闪光点:
技术能力强:在递归下降解析器的实现和表达式规范化方面展现了深厚的技术功底,能够迅速定位和解决复杂问题。
细致耐心:在代码调试和Bug修复过程中表现出极大的耐心和细致,确保每一个问题都被彻底解决。
hugh的闪光点:
算法优化:在性能优化和数据结构选择上展现出敏锐的洞察力,提出了多项优化建议,显著提升了程序的效率。
良好的沟通:在团队协作中,能够清晰地表达自己的想法和建议,促进了项目的顺利进行。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号