洛谷1099 [NOIP2007] 树网的核

链接https://www.luogu.org/problemnew/show/P1099

题目描述

设T=(V,E,W)是一个无圈且连通的无向图（也称为无根树），每条边到有正整数的权，我们称TTT为树网（treebetwork），其中V，E分别表示结点与边的集合，W表示各边长度的集合，并设T有n个结点。

路径：树网中任何两结点a，b都存在唯一的一条简单路径，用d(a,b)表示以a,b为端点的路径的长度，它是该路径上各边长度之和。我们称d(a,b)为a,ba两结点间的距离。

D(v,P)=min⁡{d(v,u)} u为路径P上的结点。

树网的直径：树网中最长的路径成为树网的直径。对于给定的树网T，直径不一定是唯一的，但可以证明：各直径的中点（不一定恰好是某个结点，可能在某条边的内部）是唯一的，我们称该点为树网的中心。

偏心距ECC(F)：树网T中距路径F最远的结点到路径FFF的距离，即

ECC(F)=max{d(v,F),v∈V}

任务：对于给定的树网T=(V,E,W)和非负整数s，求一个路径F，他是某直径上的一段路径（该路径两端均为树网中的结点），其长度不超过s（可以等于s），使偏心距ECC(F)最小。我们称这个路径为树网T=(V,E,W)的核（Core）。必要时，FFF可以退化为某个结点。一般来说，在上述定义下，核不一定只有一个，但最小偏心距是唯一的。

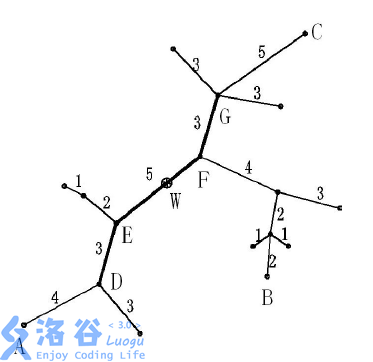
下面的图给出了树网的一个实例。图中，A−B与A−C是两条直径，长度均为20。点W是树网的中心，EF边的长度为5。如果指定s=1，则树网的核为路径DEFG（也可以取为路径DEF），偏心距为8。如果指定s=0，则树网的核为结点F，偏心距为12。

输入输出格式

输入格式：

共n行。

第1行，两个正整数n和sss，中间用一个空格隔开。其中n为树网结点的个数，s为树网的核的长度的上界。设结点编号以此为1,2,…,n

从第2行到第n行，每行给出3个用空格隔开的正整数，依次表示每一条边的两个端点编号和长度。。

输出格式：

一个非负整数，为指定意义下的最小偏心距。

输入输出样例

输入样例#1： 

5 2
1 2 5
2 3 2
2 4 4
2 5 3

输出样例#1： 

5

输入样例#2： 

8 6
1 3 2
2 3 2 
3 4 6
4 5 3
4 6 4
4 7 2
7 8 3

输出样例#2： 

5

说明

100%数据满足：5≤n≤300,0≤s≤1000

NOIP 2007 提高第四题

 

题目解读&做法

题面好长

N<=300

这个题读懂了，这样的数据范围，怎么搞都超不了时=、=，就就就能A了

本题 题中给出的定义，以及求法

（1）a到b路径的长度：所有两点间的距离通过每个点DFS求得

（2）直径（树中最长的路径）：以点A为源点，找到与他距离最远的B，再以B为源点，找到与B距离最远的C，BC之间的路径就是直径，通过一个DFS把直径上的点都拿出来存到一个数组D里

（3）核（直径上的一个子路径，题目要求他的长度小于S）：在D数组中枚举符合要求的核的两端点

（4）点到路径的距离（该点到路径上所有点的距离的最小值）：枚举路径上的所有点取最小值

（5）偏心距（所有点到核的距离的最大值）：枚举每个点，求他到核的距离取最大值

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
int read(){
    int x=0,t=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')t=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*t;
}
struct edge{int to,val;};
vector <edge> a[333];
int N,S,len[333][333],L,Ll,R,Rl,D[333],DL,dep[333],ta;
bool vis[333];
void DFS(int k,int x){　　　　　　　　　　　　　　　　　　　　//下面是三个都一样的DFS函数。
    vis[x]=1;
    for(int i=0;i<a[x].size();i++)
        if(!vis[a[x][i].to]){
            len[k][a[x][i].to]=len[k][x]+a[x][i].val;
            DFS(k,a[x][i].to);    
        }    
}
void DFS2(int x){
    for(int i=0;i<a[x].size();i++)
        if(dep[a[x][i].to]==0&&a[x][i].to!=L){
            dep[a[x][i].to]=1+dep[x];
            DFS2(a[x][i].to);    
        }
}
void findpath(int x){
    D[++DL]=x;
    if(dep[x]==0)return;
    for(int i=0;i<a[x].size();i++){
        if(dep[a[x][i].to]==dep[x]-1){findpath(a[x][i].to);
        break;
        }
    }    
}
int main()
{
    N=read(),S=read();
    for(int i=1;i<N;i++){
        int x=read(),y=read(),z=read();    
        a[x].push_back( (edge){y,z} );
        a[y].push_back( (edge){x,z} );
    }
    for(int i=1;i<=N;i++){
        memset(vis,0,sizeof vis);
        DFS(i,i);                    　　　　　　　　　　　　//每个点DFS求任意两点间的距离
    }

    for(int i=1;i<=N;i++)
        if(len[1][i]>Ll)Ll=len[1][i],L=i;
    for(int i=1;i<=N;i++)
        if(len[L][i]>Rl)Rl=len[L][i],R=i;
    DFS2(L);findpath(R);            　　　　　　　　　　　　　//找出直径

    int ans=233333333;
    for(int l=1;l<=DL;l++)
        for(int r=l;r<=DL;r++){　　　　　　　　　　　　　　　　//枚举直径上的核
        if(len[D[l]][D[r]]>S)continue;
        ta=0;
        for(int i=1;i<=N;i++){
            int dis=233333333;        
            for(int j=l;j<=r;j++)
                dis=min(dis,len[i][D[j]]);　　　　　　　　　　//计算偏心距
            ta=max(dis,ta);
        }
        ans=min(ans,ta);        
    }

    printf("%d\n",ans);
    return 0;    
}

吐槽

luogu这个题的数据十分水，我在第一次提交的时候，误把直径数组的下标当做了数值，结果还过了6个点，speakless~ （要不我就说我一遍把他A了）

（N50万 数据加强版地址： https://www.lydsy.com/JudgeOnline/problem.php?id=1999

以后再去做了他）

9.28日凌晨更新加强版数据题解 by Elfish

因为数据扩大了很多，所以我们的复杂度需要控制在O(n)，操作同样为先进行dfs寻找直径，在直径上寻找符合条件的最长路径(这样保证核的覆盖长度最大,使得偏心距最小)。

设直径起点为L终点为R，核的起点为l终点为r，那么偏心距就等于 max(dis(L,l),dis(r,R),g(i)) g(i)为直径以外的点到直径的距离，可以直接从直径上的点向直径外的点dfs求出距离

代码如下

 

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
using namespace std;
#define maxn 500005
struct edge{
    int next,to,w;
    }e[maxn*2];
int n,s;
int cnt;
int head[maxn],dis[maxn],f[maxn];
bool vis[maxn];
int fa;
void insert(int u,int v,int w){
    cnt++;
    e[cnt].next=head[u];e[cnt].to=v;e[cnt].w=w;
    head[u]=cnt;
    }
void dfs(int u,int fa){
    f[u]=fa;
    for(int i=head[u];i;i=e[i].next){
        int to=e[i].to;
        if(vis[to]||e[i].to==fa)continue;
        dis[to]=dis[u]+e[i].w;
        dfs(to,u);
        }
    }
int l,r;
void getd(){
    l=1;r=1;
    memset(vis,0,sizeof vis);
    dfs(l,0);
    for(int i=1;i<=n;i++)if(dis[i]>dis[r])r=i;
    l=r;
    dis[r]=0;
    dfs(r,0);
    for(int i=1;i<=n;i++)if(dis[i]>dis[l])l=i;
    }
int main(){
    scanf("%d%d",&n,&s);
    int u,v,w;
    for(int i=1;i<n;i++){
        scanf("%d%d%d",&u,&v,&w);
        insert(u,v,w);
        insert(v,u,w);
        }
    getd();
    int j=l,ans=500000000;
    for(int i=l;i;i=f[i]){
        while(f[j]&&dis[i]-dis[f[j]]<=s) j=f[j];
            ans=min(ans,max(dis[j],dis[l]-dis[i]));
     }
//    printf("%d %d %d %d\n",l,r,ans,dis[l]);
//    for(int i=l;i;i=f[i])printf("%d ",dis[i]);
    for(int i=l;i;i=f[i])vis[i]=1;
    for(int i=l;i;i=f[i]){
        dis[i]=0;dfs(i,f[i]);
        }
    for(int i=1;i<=n;i++)ans=max(ans,dis[i]);
    printf("%d",ans);
//    system("pause");
    return 0;
    }