bzoj 1088 [SCOI2005] 扫雷

SCOI2005 扫雷

一道很有趣的(水)题

“这道题有四种解法，你知道么”

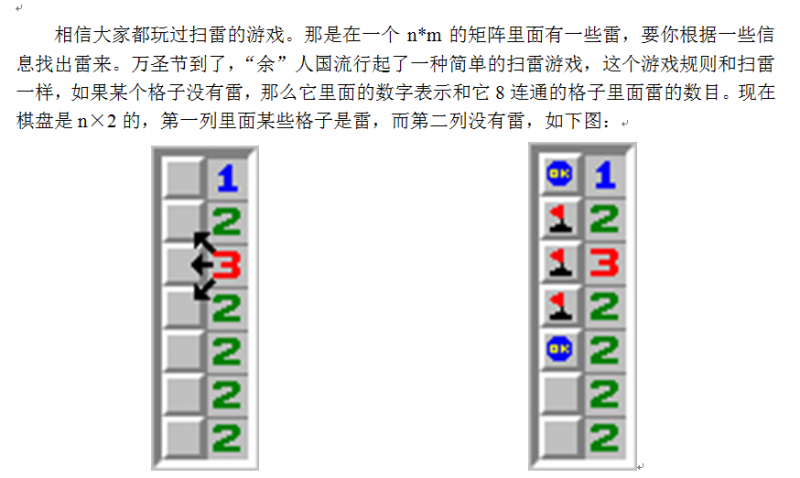
给你矩阵的第二列的数字，求出第一列雷有多少种可能的摆法。

不懂扫雷规则的自行按win+R然后输入winmine

思考过后我想到了一种拙劣的DP写法 ，

四维 F[i][][][] i代表到了第几个格子，后面三维用 0和1表示 这个格子旁边雷的情况，分别是 左上 左 左下

简单易懂(十分恶心)的代码

#include<bits/stdc++.h>
using namespace std;
int N,a[10010],f[10010][2][2][2];
int main()
{
    ios::sync_with_stdio(false);
    cin>>N;
    for(int i=1;i<=N;i++)cin>>a[i];
    if        (a[1]==0)f[1][0][0][0]=1;
    else if    (a[1]==1)f[1][0][1][0]=1,f[1][0][0][1]=1;
    else if    (a[1]==2)f[1][0][1][1]=1;
    for(int i=2;i<=N-1;i++)
    {
        if        (a[i]==0)
            f[i][0][0][0]=f[i-1][1][0][0]+f[i-1][0][0][0];
        else if    (a[i]==1)
            f[i][1][0][0]=f[i-1][0][1][0]+f[i-1][1][1][0],
            f[i][0][1][0]=f[i-1][1][0][1]+f[i-1][0][0][1],
            f[i][0][0][1]=f[i-1][0][0][0]+f[i-1][1][0][0];
        else if    (a[i]==2)
            f[i][1][1][0]=f[i-1][1][1][1]+f[i-1][0][1][1],
            f[i][1][0][1]=f[i-1][0][1][0]+f[i-1][1][1][0],
            f[i][0][1][1]=f[i-1][1][0][1]+f[i-1][0][0][1];
        else if    (a[i]==3)
            f[i][1][1][1]=f[i-1][1][1][1]+f[i-1][0][1][1];
    }
    if        (a[N]==0) cout<<f[N-1][1][0][0]+f[N-1][0][0][0];
    else if    (a[N]==1) cout<<f[N-1][1][0][1]+f[N-1][0][0][1]+f[N-1][0][1][0]+f[N-1][1][1][0];
    else if    (a[N]==2) cout<<f[N-1][1][1][1]+f[N-1][0][1][1];
    return 0;    
} 

就是枚举出了所有的情况 ，暴力转移。  (手边要有个画图板 边写边画 别漏情况)

美其名曰DP

当时代码写得十分顺，一遍过编译 ，一遍AC 

 

实际上 ，没这么复杂。

现在我们可以思考一下 ， 第二列数字都已知 ， 如果你知道了第一列的前两个格子是否有雷 ，那么 我们就可以把 所有的 都推出来了 

b[i]=a[i-1]-b[i-1]-b[i-2] (b[i]是格子i的雷，a[i]是第二列的数字)

所以只要枚举前两个格子的雷就可以了 。

这题答案只有 0，1，2；

超短代码↓

#include<bits/stdc++.h>
using namespace std;
int N,a[10010],ans;
void Work(int x,int y)
{
    int b[10010];
    b[1]=x,b[2]=y;
    for(int i=3;i<=N+1;i++)
        b[i]=a[i-1]-b[i-1]-b[i-2];
    if(b[N+1]==0)ans++;
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>N;
    for(int i=1;i<=N;i++)cin>>a[i];
    if        (a[1]==1)Work(0,1),Work(1,0);
    else if    (a[1]==2)Work(1,1);
    else if (a[1]==0)Work(0,0);
    cout<<ans<<endl;
    return 0;
}