凯撒Cezar
题意
这题首先需要读懂题:给出的序列 \(A_i\) 代表第 \(i\) 个字符串排名为 \(A_i\)
拿样例1来说,就是:第二个字符串 "\(bc\)" 排名为1,第一个字符串 "\(ab\)" 排名为2(说明 "\(bc\)" 这个字符串的字典序比 "\(ab\)" 小)
(好像很多人都理解错了)
思路
这题,一眼拓扑(或者变种 \(Floyd\))
- 转换
首先,根据序列 \(A_i\) 我们可以进行字符之间的连边——确定字典序大小关系(排在前面的连向排在后面的)
然后我们就将字符串间的关系转化为有向图,那么接下来就是赤裸裸的拓扑了啊!
- 拓扑
这里会遇到第一个无解(即 "\(NE\)")的情况:跑拓扑的时候,一开始队列就为空(说明不存在入度为0的点,则形成了环)
判了上面这种情况,接下来就是拓扑板子。用 \(ans\) 和 \(ans2\) 记录拓扑序,用 \(viss\) 标记这个点被找到过
接下来,我们将 \(ans\) 从小到大排序,再将 \(ans\) 和 \(ans2\) 一一对应存入 \(anss\) 中(最终输出的数组)。我们根据下面的图来理解为什么排序后直接对应即可:
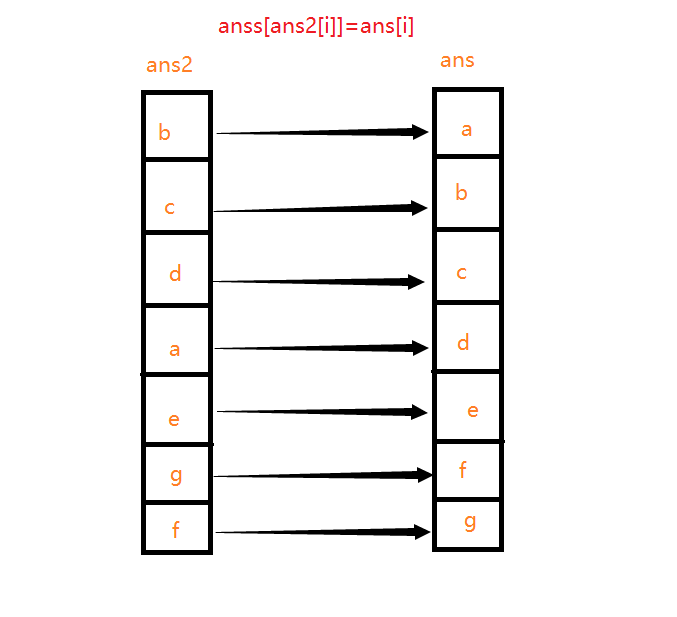
应该可以理解吧?如果不是很清楚的话,可以把样例1、3都画一下
对应的代码段就是:
sort(ans+1,ans+1+sum);
for(int i=1;i<=sum;i++) {
anss[ans2[i]]=ans[i];
}
for(int i=0;i<=25;i++) {
if(vis[i]&&!viss[i]) {
puts("NE");
return 0;
}
if(!viss[i]) anss[i]=i;
}
- 无解
因为这题是SPJ,所以当跑拓扑序的时候可以一次多点入队
然后就是比较极端的两组数据(还是比较考细节吧):
5
c
cc
ccc
cccc
ccccc
1 2 3 4 5
out:
DA
abcdefgihjklmnopqrstuvwxyz
5
d
dd
ddd
dddd
ddddd
1 2 3 5 4
out:
NE
发现区别了吗?
第一组数据是因为所有字符串都是相同的一个字符,且排名在前的字符串的长度永远不大于排名在后的字符串
而第二组数据就是这里出锅,所以是 "\(NE\)" (排名第四的字符串长度大于排名第五的字符串)
那么我们就可以在跑拓扑之前特判一下这两种情况:
设 \(cnt\) 记录有多少个不同的字符
-
若 \(cnt==1\),且 \(len[i]>len[j](i<j)\),则是上面第二组数据的情况,输出无解
-
连完边后,再判断若 \(cnt==1\) ,则是上面第一组数据的情况,直接输出有解然后结束程序即可
还有一种无解的情况就是:若跑完拓扑序后发现,原本是有大小关系的字符而没有在拓扑序中出现,那么也是无解,即:
for(int i=0;i<=25;i++) {
if(vis[i]&&!viss[i]) { //vis标记在大小关系比较中出现过的点
puts("NE");
return 0;
}
if(!viss[i]) anss[i]=i;
}
代码
嗯,思路和需要注意的细节就是上面讲的这么多了,接下来直接看代码吧:
#include <bits/stdc++.h>
using namespace std;
string s[1001];
int sum,vis[1001],viss[1001],ans[20010],ans2[20010];
int n,tot,cnt,a[1001],in[1001],head[200010],anss[20010];
struct node {
int to,net;
} e[200010];
void add(int u,int v) {
e[++tot].to=v;
e[tot].net=head[u];
head[u]=tot;
}
int topo() {
queue<int> q;
for(int i=0;i<=25;i++) {
if(!in[i]&&vis[i]) q.push(i);
}
if(!q.size()) return -1;
while(!q.empty()) {
bool flag=false;
int x=q.front();
q.pop();
if(viss[x]) return -1;
viss[x]=1;
ans[++sum]=x;
ans2[sum]=x;
for(int i=head[x];i;i=e[i].net) {
int v=e[i].to;
if(--in[v]==0) {
flag=true;
q.push(v);
}
}
}
return sum;
}
int main() {
scanf("%d",&n);
for(int i=1;i<=n;i++) {
cin>>s[i];
}
for(int i=1;i<=n;i++) {
scanf("%d",&a[i]);
}
for(int i=1;i<n;i++) {
int k=0,kk=0;
while(k<s[a[i]].size()&&kk<s[a[i+1]].size()) {
if(s[a[i]][k]!=s[a[i+1]][kk]) {
add(s[a[i]][k]-'a',s[a[i+1]][kk]-'a');
if(!vis[s[a[i]][k]-'a']) cnt++,vis[s[a[i]][k]-'a']=1;
if(!vis[s[a[i+1]][kk]-'a']) cnt++,vis[s[a[i+1]][kk]-'a']=1;
in[s[a[i+1]][kk]-'a']++;
break;
}
k++;kk++;
}
if(cnt==0&&s[a[i]].size()>s[a[i+1]].size()) {
puts("NE");
return 0;
}
}
if(cnt==0) {
puts("DA");
for(int i=0;i<=25;i++) cout<<char(i+'a');
return 0;
}
int t=topo();
if(t==-1) {
puts("NE");
return 0;
}
sort(ans+1,ans+1+sum);
for(int i=1;i<=sum;i++) {
anss[ans2[i]]=ans[i];
}
for(int i=0;i<=25;i++) {
if(vis[i]&&!viss[i]) {
puts("NE");
return 0;
}
if(!viss[i]) anss[i]=i;
}
puts("DA");
for(int i=0;i<=25;i++) {
cout<<char(anss[i]+'a');
}
return 0;
}


