Word Rings
Word Rings
前言
说实话,这题一看我还真没思路(是我太菜)
在草稿本上写写画画了一点时间,就有了一点思路,好了,开始讲题
算法
二分答案 & \(SPFA\)(\(dfs\)版)
\(SPFA\)
没思路,就来看样例,如图:
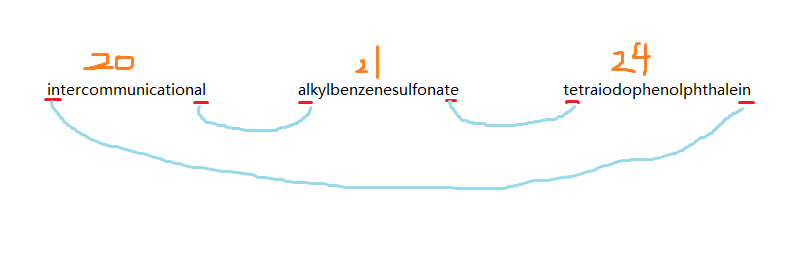
我们发现,两个能相连的字符串\(A\)、\(B\),看的只有\(A\)的前后两个字符和\(B\)的前后两个字符,中间的冗余字符其实并不重要,因为我们需要的只是整个字符串的长度而已
所以我们何必留下冗余无用的字符呢?所以我们可以把上图简化为下图(有点丑,见谅啊qwq):
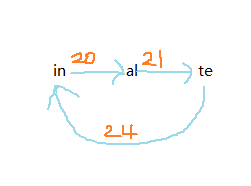
有点图论的思路了吗?
即:
-
将每个字符串的前两个字符和后两个字符当做一个节点
-
将每个字符串的长度当做这两个节点的边权,然后将它们连起来
于是我们就构建出了如上的图(2)
那么剩下的就是找环了,这时我们一般会想到:遍历整个图,找到每一个环,然后算出它们的平均值,最后比较出最大值
但是这题多组数据,还不说图的大小,所以这种思路肯定会T飞的
那怎么做?——不能找环,那我们就直接找答案啊!(这里要转换一下思想)
找实数域的答案,那第一个想到的肯定就是实数域上的二分答案!
二分答案
不懂的,可以看看二分答案的讲解
然后这里我们直接来讨论为什么以及怎么二分答案
我们能将求答案\(ans\)的式子表示如下:
\(ans=(len_1+len_2+len_3+···+len_k)/K\)
数学转换一下:
\(ans*K=len_1+len_2+len_3+···+len_k\)
移项一下:
\((len_1+len_2+len_3+···+len_k)-ans*k=0\)
最后我们可得:
\((len_1-ans)+(len_2-ans)+(len_3-ans)+···+(len_k-ans)≥0\)
为什么是\(≥\)?因为最开始的式子是整除,会有精度问题,所以是\(≥\)
代码\(Code\)
好了,二分答案和\(SPFA\)的思路就是如上这么多了,现在贴一发代码吧
#include <bits/stdc++.h>
using namespace std;
string s;
double ans,dis[520010];
int n,tot,vis[520010],head[520010];
struct node {
int to,net,val;
} e[520010];
inline void add(int u,int v,int w) {
e[++tot].to=v;
e[tot].val=w;
e[tot].net=head[u];
head[u]=tot;
}
inline bool dfs(int now,double x) { //dfs版的SPFA
vis[now]=1;
for(register int i=head[now];i;i=e[i].net) {
int v=e[i].to;
if(dis[v]<dis[now]+e[i].val-x) {
dis[v]=dis[now]+e[i].val-x;
if(vis[v]==1||dfs(v,x)==true) return true;
}
}
vis[now]=0;
return false;
}
inline bool check(double x) {
memset(dis,0,sizeof(dis));
memset(vis,0,sizeof(vis));
for(register int i=1;i<=1000;i++) {
if(dfs(i,x)==true) return true;
}
return false;
}
int main() {
while(scanf("%d",&n)) {
if(n==0) break;
tot=0;
memset(head,0,sizeof(head));
for(register int i=1;i<=n;i++) {
cin>>s;
int len=s.length();
int u=(s[0]-'a')*26+(s[1]-'a')+1; //将字符转换为节点连边
int v=(s[len-2]-'a')*26+(s[len-1]-'a')+1;
add(u,v,len);
}
double l=0,r=1000;
while(r-l>1e-4) { //二分答案
double mid=(l+r)/2.0;
if(check(mid)==true) {
l=mid;
}
else r=mid;
}
if(l==0) puts("No solution.");
else printf("%.2lf\n",l);
}
return 0;
}
最后,如果这篇题解有任何问题或您有任何不懂,欢迎在下面留言区评论,我会及时回复、改正,谢谢各位dalao啊qwq


