玛丽卡
玛丽卡
题目简述
不得不吐槽一下,这道题的题目描述真的有毒,读完题满脸懵QAQ(也可能因为我菜)
就根据我自己的理解来转述一下题意吧(可能也不清楚,轻喷啊)
给定\(N\)个城市和\(M\)条道路,对于每条路,给定连接的两个城市编号以及通过这条路所花费的时间,再告诉你在某一时刻有一条路可能会堵车
要求找到一个\(t\)满足:
-
在\(t\)时刻内,无论哪一条道路堵车(即不能走),你都能找到一条从\(1\)到\(N\)的路径,且这条路径所花费的总时长一定\(≤t\)
-
但是任意小于\(t\)的值\(t'\),都存在至少一种情况使得若有一条路堵车,那么则无法找到一条从\(1\)到\(N\)的路径,满足这条路径所花费的总时长一定\(≤t'\)
但是这题还是良心的,它不卡SPFA!!
还是要提醒一下,这道题最后一个点的\(M\)有\(2*10^5\),所以数组要开大一点
解题思路
还是有点绕?那我们来分析一下样例吧:
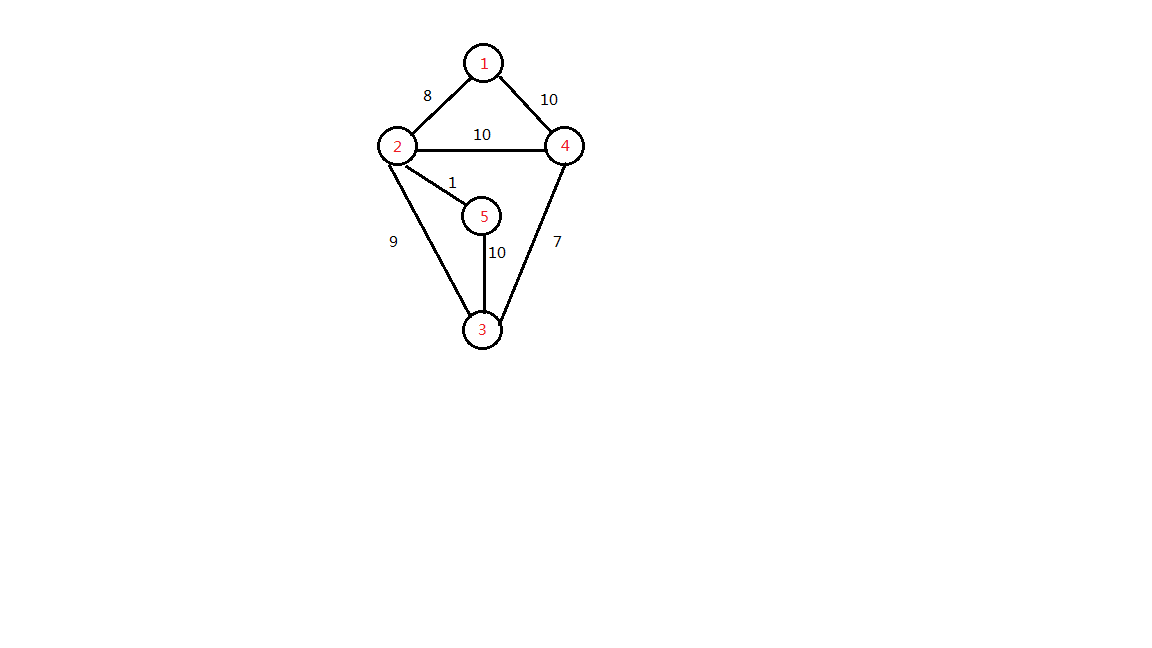
直接求最短路肯定是:1->2->5,最短时间花费总和则是:8+1=9
但是根据题意,可能会有一条路堵车:假设2->5这条路堵车了,那么在9分钟内我们显然无法找到一条从\(1\)到\(N\)的路径,所以9这个答案是错误的
所以直接跑最短路是错误做法,接下来来讲解一下正解
- 模拟堵车(删边)
因为一旦堵车那么那一条路我们就不能走,所以堵车=不能走=删边
没有直接的解题思路,那我们就先来手模一遍样例的删边操作:
删1->2(8):最短时间21
删1->4(10):最短时间9
删2->4(10):最短时间9
删2->5(1):最短时间27
删2->3(9):最短时间9
删3->5(10):最短时间9
删3->4(7):最短时间9
找到了吗?样例输出的\(27\)就在我们上面的删边操作里面
好像有点思路了:我们模拟依次删除每一条边,然后跑一边最短路找到当前对应的最短时间,最后在所有最短时间中找到最大值,就是我们的答案
- 思路优化
将上面的初步思路实现为代码,我们只能得到50pts~80pts(\(Dijkstra\) 50pts,\(SPFA\) 80pts),其余的点都是TLE
得到一大部分分但是超时了,说明我们的思路缺少优化
再来分析样例,我们从上面的删边操作模拟就会发现,只有删边\(1->2\)或\(2->5\)最短时间才会发生变化,删其他边得到的结果依旧是最开始的最短路径
为什么呢?因为删其他边很明显不会影响到原来的最短路径啊!
所以我们删边只需要在原始的最短路径上进行即可
代码Code
- 先上AC代码(思路优化版)
#include <bits/stdc++.h>
using namespace std;
int n,m,u,v,w,tot,ans,summ,sum[5000010];
int dis[5000010],vis[5000010],pre[5000010],head[5000010];
priority_queue<pair<int,int> > shan;
struct node {
int to,net,val;
} e[5000010];
inline void add(int u,int v,int w) {
e[++tot].to=v;
e[tot].val=w;
e[tot].net=head[u];
head[u]=tot;
}
inline void dijkstra(int xx,int yy) {
for(register int i=1;i<=n;i++) {
vis[i]=0;
pre[i]=0;
dis[i]=20050206;
}
dis[1]=0;
shan.push(make_pair(0,1));
while(!shan.empty()) {
int x=shan.top().second;
shan.pop();
if(vis[x]) continue;
vis[x]=1;
for(register int i=head[x];i;i=e[i].net) {
int v=e[i].to;
if(x==xx&&v==yy) continue;
if(dis[v]>dis[x]+e[i].val) {
dis[v]=dis[x]+e[i].val;
pre[v]=x;
shan.push(make_pair(-dis[v],v));
}
}
}
}
int main() {
scanf("%d%d",&n,&m);
for(register int i=1;i<=m;i++) {
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
add(v,u,w);
}
dijkstra(0,0);
int k=n;
while(k) {
sum[++summ]=k;
k=pre[k];
}
for(register int i=summ;i>1;i--) {
dijkstra(sum[i],sum[i-1]);
ans=max(ans,dis[n]);
}
printf("%d",ans);
return 0;
}
- 再来基础思路版的未AC代码
#include <bits/stdc++.h>
using namespace std;
int n,m,tot,ans,u[50010],v[50010],w[50010];
int dis[50010],vis[50010],head[50010];
struct node {
int to,net,val;
} e[50010];
inline void add(int u,int v,int w) {
e[++tot].to=v;
e[tot].net=head[u];
e[tot].val=w;
head[u]=tot;
}
inline void spfa(int xx,int yy) {
queue<int> shan;
for(register int i=1;i<=n;i++) {
vis[i]=0;
dis[i]=20050206;
}
dis[1]=0;
vis[1]=1;
shan.push(1);
while(!shan.empty()) {
int x=shan.front();
shan.pop();
vis[x]=0;
for(register int i=head[x];i;i=e[i].net) {
int v=e[i].to;
if(x==xx&&v==yy) continue;
if(dis[v]>dis[x]+e[i].val) {
dis[v]=dis[x]+e[i].val;
if(vis[v]==0) {
shan.push(v);
vis[v]=1;
}
}
}
}
}
int main() {
scanf("%d%d",&n,&m);
for(register int i=1;i<=m;i++) {
scanf("%d%d%d",&u[i],&v[i],&w[i]);
add(u[i],v[i],w[i]);
add(v[i],u[i],w[i]);
}
for(register int i=1;i<=m;i++) {
spfa(u[i],v[i]);
if(dis[n]!=20050206) ans=max(ans,dis[n]);
}
printf("%d",ans);
return 0;
}
最后,感谢一下ZJY大佬提供的思路优化


