无向二分图 TSP 的 $1.9999^n$ 算法与矩阵乘法 (鸽了)
2020 年, Nederlof 提出了一个假设 \(\omega=2\) 的情况下, 在 \(O(1.9999^n)\) 时间内计算无向二分图 TSP 的算法.
这个玩意真的是有点外星科技的感觉了. 我试图大概解释清楚它的思路是啥, 某些技术细节就算了...
首先, 我们知道 Björklund 在较早的时候就给出了一个漂亮的 \(O^*(2^{n/2})\) 判断无向二分图的 Hamilton 路的算法, 但这个算法是代数的, 如果想用来做 TSP 也不是不行, 但是会直接带一个 \(W\) 的因子. 如果想把这个 \(W\) 变成 \(\log W\), 已有的那些代数算法对此尚无头绪.
Nederlof 的做法仍然用到了代数算法, 但是却是另一条思路的产物. 按照我的理解顺序, 我们倒过来讲这个过程.
基本思想: Hamilton 路的匹配分解
首先注意到对于二分图上的一个 Hamilton 路, 我们可以直接将这条路径拆成两个完美匹配的并 \(A\cup B\). 现在我们倒过来考虑这个问题: 设 \(\mathcal P\) 是全体完美匹配构成的族, 我们就希望找两个 \(A, B\in \mathcal P\), 使得 \(A, B\) 确实构成一个 Hamilton 路, 在这个限制的条件下最小化 \(w(A) + w(B)\).
我们记 \(H[A, B]\) 表示 \(A, B\) 是否构成 Hamilton 路, 那么如果我们想考虑两个 \(\mathcal P\) 的子集 \(\mathcal {A, B}\) 之间是否有 \(A, B\) 构成 Hamilton 路的话, 就等于是问 \(H\) 限制在 \(\mathcal A\times \mathcal B\) 上是否是全零矩阵.
我们知道, 要想知道一个矩阵 \(M\) 是否全零, 有一个简单的概率方法就是选取两个随机向量 \(u, v\), 然后计算 \(u^\mathsf{T} M v\) 是否为 \(0\).
庆幸的是, \(H\) 有一些非常美好的性质, 让这种检测方式有快速计算的可能.
另一个就是约化 \(\mathcal A\) 的大小, 我们知道, 全体完美匹配有 \((n-1)!!\) 种, 这比指数还多. 但事实上, 可以用一些手段将备选的答案降低到 \(2^{n/2}\) 个.
匹配分解的矩阵分解
我们考虑域为 \(\mathbb F_2\). 在特征为 \(2\) 的域上, 我们首先有第一种 \(H\) 的分解方式:
割分解 (Cut Factorization). 对于集合 \(S\) 和匹配 \(A\), 我们记向量 \(v^{(S)}\) 的第 \(A\) 项为 \(1\) 当且仅当 \(A\) 没有被 \(S\) 割开. 那么 Hamilton 路矩阵有分解
\[H = \sum_{1\in S} v^{(S)}(v^{(S)})^{\mathsf T} . \]
证明. 选取任一组 \(A, B\) 考察这个求和, 显然 \(S\) 贡献 \(1\) 的位置就是 \(S\) 即没割开 \(A\) 又没割开 \(B\). 这样的方案恰有 \(2^{c - 1}\) 种, \(c\) 是环的数量. 那么只有 \(c=1\) 的时候没抵消. \(\square\)
于是我们能够得到如下算法:
定理. 给定一些完美匹配构成的族 \(\mathcal A\), 可以在 \(O^*(|\mathcal A| 2^{n/2} + 2^n)\) 的时间内判断是否存在两个元素 \(A, B\in \mathcal A\) 满足 \(H[A, B] = 1\).
证明. 我们随机定义域在 \(\mathcal A\) 上的向量 \(u, v\), 然后只需要计算
那么我们首先对每个 \(S\) 计算出 \(u^{\mathsf T} v^{(S)}\) 和 \(v^{\mathsf T} v^{(S)}\).
首先, 这个 \(O(2^n)\) 的部分就来源于最后的点乘.
那么 \(O(|\mathcal A| 2^{n/2})\) 是怎么回事呢? 注意对于每个 \(A\), 我们只需要对于 \(v^{(S)}[A] = 1\) 的 \(S\) 提供贡献. 这样的 \(S\) 有多少个呢? 注意 \(A\) 的每个连通块的 \(S\) 要么全选要么全不选, 所以这样的 \(S\) 有 \(2^{n/2}\) 种. 一次这样的实验有 \(3/4\) 的单侧错误率, 所以 \(n^{O(1)}\) 次就可以得到指数级别的错误率. 这样就得到了复杂度 \(O^*(|\mathcal A| 2^{n/2} + 2^n)\). \(\square\)
注意这个算法的判定方式是极为简单的, 所以它可以很容易地转化成解决带权问题的版本.
定理. 给定一些完美匹配构成的族 \(\mathcal A\), 其中每个匹配赋予一个权值, 可以在 \(O^*(|\mathcal A| 2^{n/2} + 2^n)\) 的时间内找到最小权的元素 \(A, B\in \mathcal A\) 满足 \(H[A, B] = 1\).
证明. 先把 \(\mathcal A\) 里的元素排序, 考虑排成 \(A_1 \leq A_2\leq \cdots \leq A_k\). 我们做一个双指针, 维护 \(p, q\) 两个指针, 让 \(p\) 不断减小的时候, 我们维护最小的 \(q\) 使得 \(A_{1\sim p}\) 和 \(A_{1\sim q}\) 之间有一对能配成 Hamilton 路.
注意到维护这个每次只需要给两侧的 \(u, v\) 做均摊 \(O(1)\) 次修改, 对应的在点积序列上只有 \(O(2^{n/2})\) 的修改, 所以复杂度不变. \(\square\)
但目前的复杂度是不行的, 已经超过 \(1.9999^n\) 了. 事实上, \(H\) 不仅有这一种分解方式.
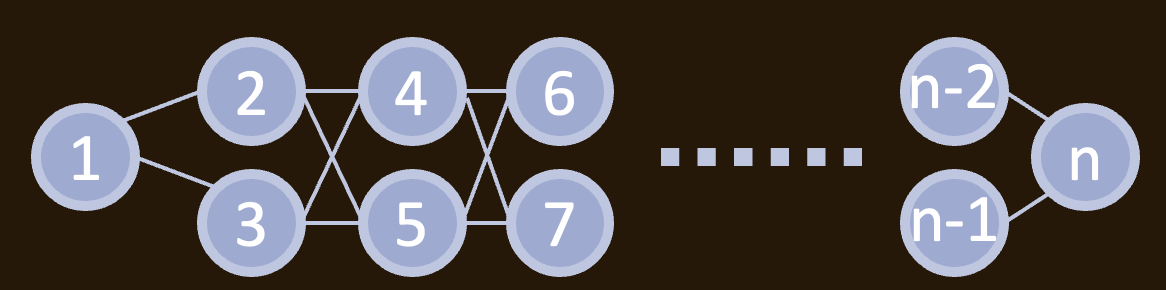
匹配分解 (Matching Factorization).
设 \(\mathcal P_n\) 是下图的所有完美匹配:
那么有 \(\mathbb F_2\) 上的等式\[H[A, B] = \sum_{P\in \mathcal P_n} H[A, P] H[\overline{P}, B]. \]其中 \(\overline{P}\) 是某个对合, 暂略.
证明就略了.
我们可以看到, \(|\mathcal P_n| = 2^{n/2-1}\), 所以沿用前面的做法, 可以做到 \(O^*(|\mathcal A| 2^{n/2} + 2^{n/2})\) 的复杂度, 但我们 \(|\mathcal A|\) 的大小预计也有 \(2^{n/2}\), 所以依然是不够的.
另外, 可以证明 \(H\) 矩阵在 \(\mathbb F_2\) 上的秩也是 \(2^{n/2-1}\).
为了进一步解决这个问题, Nederlof 引入了第三种分解方式: 狭窄割分解 (Narrow Cut Factorization), 通过一种复杂的挤水方法, 结合了前面两种结构, 再用了一些随机化方法来做剪枝. 总之, 他做到了 \(O^*(|\mathcal A|2^{0.3n} + 3^{n/2})\) 的复杂度计算前面描述的问题.
至此, 这部分将会在最终复杂度里不作为瓶颈, 且带入 \(\mathcal |A| = 2^{n/2}\), 这部分单独的复杂度是 \(O^*(2^{0.9 n})\).
处理代表集合
首先让我们获取一些 intuition, 关于为什么可以让把超指数的完美匹配先剪枝成只剩下 \(2^{n/2}\) 个.
首先我们考虑判定性问题. 注意到对于矩阵 \(H[\mathcal A, \mathcal B]\), 如果我们对于任何一个询问 \(B\in \mathcal B\) 试图找一个 \(A\in \mathcal A\) 的话, 可以考虑适当的缩小 \(\mathcal A\) 的大小, 找到一个 \(\mathcal A' \subseteq \mathcal A\), 使得只要 \(\mathcal A\) 有解则 \(\mathcal A'\) 有解. 这样的 \(\mathcal A'\) 被称为 代表集合 (representative set), 这也是 参数算法 (parametrized algorithm) 中的常用概念.
注意限制在 \(H[\mathcal A, \mathcal B]\) 这个矩阵上的话, 考虑此时行向量的一组基 \(\mathcal A'\), 容易证明它是能满足所有解的, 所以我们发现一个惊人的事实: 对于判定问题, 只需要保留 \(\leq \operatorname{rank} H \leq 2^{n/2-1}\) 个完美匹配即可. 最后一个不等式由匹配分解支持.
(剩下的先鸽着, 太外星了)