另一种特征多项式算法

在 OI 中，比较普及的求解矩阵的特征多项式的算法是这个，在阅读一些文献后，这里给出另一种可实现的做法，不过从实测结果来看不是很有优势。

对于给定的矩阵 \(A\) 和向量 \(v\)，我们设 \(p\) 是最大的正整数使得 \(\{v,Av,\dots,A^{p-1}v\}\) 线性无关。事实上，\(\mathcal K_r(A,v)=\operatorname{span}\{v,Ap,\dots,A^{p-1}v\}\) 被称为 Krylov 子空间。

如果 \(p=n\)，我们设 \(K = \begin{pmatrix} v & Av & A^2v & \cdots & A^{p-1}v \end{pmatrix}\)，那么就有 \(AK=\begin{pmatrix} Av & A^2v & A^3v & \cdots & A^pv \end{pmatrix}\)。那么进一步就有

\[K^{-1}AK = \begin{pmatrix} & & & & *\\ 1 & & & & *\\ & 1 & & & \vdots\\ & & \ddots & & \vdots\\ & & & 1 & * \end{pmatrix}\]

这种矩阵的特征多项式是很显然的。但是另一方面也很显然，对于任意的 \(A\)，这样的向量肯定是不一定存在的，比如 \(A\) 的最小多项式不是特征多项式的时候。那我们这个时候怎么办呢？

我们令 \(V\) 为当前所有向量张成的线性空间，选取 \(V\) 外一个向量 \(u\)，继续尝试加入 \(u, Au,\dots\)，直到又得到一个在原来空间内的向量，这时我们再次选一个新的 \(V\) 以外的向量继续做……最后，我们得到一个形如这样一个线性无关的向量序列：

\[v_1, Av_1,\dots,A^{p_1-1}v_1, v_2, \dots, A^{p_2-1}v_2, \dots, v_k,\dots,A^{p_k-1}v_k \]

它同时还满足 \(A^{p_i}v_i\) 能被前面的向量表出。我们这些向量并排得到矩阵 \(K\)，那么这时，\(K^{-1}AK\) 就形如下图这样：

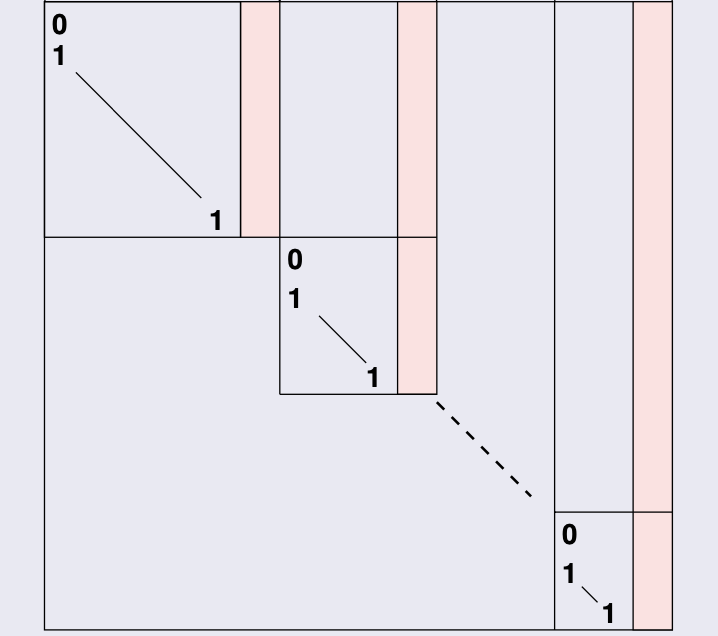
显然，整个矩阵的特征多项式也就是对角线上每个块的特征多项式之乘积了。

具体来说，我们有如下流程：

1. 维护一个线性无关组 \(S\)，初始为空。特征多项式 \(p(t)\) 初始为 \(1\)。
2. 按照 \(i=1,\dots,n\) 的顺序考虑单位向量 \(e_i\)，设为 \(v\)，不断给 \(S\) 插入 \(v,Av,\dots\)，直到得到一个 \(A^pv\) 已经能被 \(S\) 线性表出，通过高斯消元得到系数 \(A^pv - c_1 A^{p-1}v - \cdots - c_p v \in \operatorname{span}\{\mathrm{previous \, vectors}\}\)。此时将 \(p(t)\) 乘以 \(t^p - c_1 t^{p-1} - \cdots - c_p\)。

代码实现

#include <bits/stdc++.h>

using namespace std;

using ull = unsigned long long;

const int P = 998244353;

int norm(int x) { return x >= P ? x - P : x; }
int reduce(int x) { return x < 0 ? x + P : x; }
int neg(int x) { return x ? P - x : 0; }
void add(int& x, int y) { if ((x += y - P) < 0) x += P; }
void sub(int& x, int y) { if ((x -= y) < 0) x += P; }
void fam(int& x, int y, int z) { x = (x + y * (ull)z) % P; }
int mpow(int x, unsigned k) {
	if (k == 0) return 1;
	int ret = mpow(x * (ull)x % P, k >> 1);
	if (k & 1) ret = ret * (ull)x % P;
	return ret;
}
int quo2(int x) { return ((x & 1) ? x + P : x) >> 1; }

const int _ = 510;

int mat[_][_], bas[_][_], coe[_][_];
int vec[_], elim[_], tmp[_], pol[_];

int main() {
	ios::sync_with_stdio(false); cin.tie(NULL);

	int N; cin >> N;
	for (int i = 1; i <= N; ++i) for (int j = 1; j <= N; ++j) cin >> mat[i][j];

	pol[0] = 1;
	int dim = 0;
	for (int i = 1; i <= N; ++i) {
		memset(vec, 0, sizeof(vec)); vec[i] = 1;
		int lst = dim;
		while (true) {
			int id = dim + 1;
			memset(tmp, 0, sizeof(tmp));
			tmp[id] = 1;
			memcpy(elim, vec, sizeof(elim));
			bool fl = false;
			for (int j = 1; j <= N; ++j)
				if (elim[j]) {
					if (bas[j][j]) {
						int c = reduce(-elim[j]);
						for (int k = 1; k <= N; ++k) fam(elim[k], c, bas[j][k]);
						for (int k = 1; k <= N; ++k) fam(tmp[k], c, coe[j][k]);
					} else {
						fl = true;
						int c = mpow(elim[j], P - 2);
						for (int k = 1; k <= N; ++k) elim[k] = elim[k] * (ull)c % P;
						for (int k = 1; k <= N; ++k) tmp[k] = tmp[k] * (ull)c % P;
						memcpy(bas[j], elim, sizeof(elim));
						memcpy(coe[j], tmp, sizeof(tmp));
						break;
					}
				}
			if (!fl) {
				for (int j = dim; j; --j) for (int k = 1; k <= min(dim - lst, j); ++k)
					fam(pol[j], pol[j - k], tmp[dim + 1 - k]);
				break;
			}
			for (int j = 1; j <= N; ++j) {
				tmp[j] = 0;
				for (int k = 1; k <= N; ++k) fam(tmp[j], mat[j][k], vec[k]);
			}
			memcpy(vec, tmp, sizeof(tmp));
			++dim;
		}
		if (dim == N) break;
	}
	reverse(pol, pol + N + 1);
	for (int i = 0; i <= N; ++i) cout << pol[i] << " \n"[i == N];

	return 0;
}