C. Ancient Berland Circus（Codeforces Beta Round #1）

题目描述

 

 

 思路&&感想

　　这是我第一次碰到如此纯正的数学题，之前的数学题的本体还都是思维题

　　也就是这个题，让我发现高中数学真是重要

　　题目大意就是给出一个正多边形的三个顶点，之后求这个正多边形的最小面积

　　具体思路如下：

　　1.首先找到正多边形的外接圆半径R，同时也是这三个点围成的三角形的外接圆半径

　　　　通过R=(a×b×c)/(4×S),   S=sqrt(p(p-a)(p-b)(p-c))  来求解

　　2.找到外接圆的圆心和三条边（三条弦）构成的三个圆心角，如果连接三个顶点和圆心，分成的三角形的三个部分中，每个部分都包含若干个小三角形（也就是把外接圆圆心和多边形所有顶点全部相连切割成的三角形）

　　3.这三个圆心角的最大公约数（gcd是浮点数），便是每个上述小三角形的一个内角，由此可以求出每个小三角形的面积以及整个正多边形有多少个类似的小三角形，累加和

知识点

　　1.三角形的外接圆半径公式：

　　

 

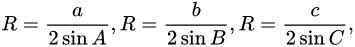
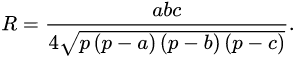　　其中

 

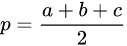
　　海伦公式：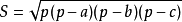

 

 

 　　2.对浮点数求最大公约数的方法

double fgcd(double a,double b)
{
    if(b<eps) return a;
    else return fgcd(b,fmod(a,b));
}

　　其实和求gcd的思路一样，也是用辗转相除法，但是要人工设置一个精度，即eps，这个精度要因题而论

　　而It's guaranteed that the number of angles in the optimal polygon is not larger than 100.给了我们思路

　　要知道fgcd的结果返回值是一定大于精度eps的，可以和gcd类比

　　而弧度越小，多边形的边数越多，而题目要求不能大于100条边

　　而2PI/100≈0.06283185307179587

　　也就是说我们所的到弧度不应该大于0.06，所以我们将精度设置为1e-2

　　但是更合理的设置精度的大小应该为6e-2，也是可以AC的但是改为7e-2后就WA掉了

　 3.fmod函数

　　C 库函数 double fmod(double x, double y) 返回 x 除以 y 的余数。

　　

#include <stdio.h>
#include <math.h>

int main ()
{
   float a, b;
   int c;
   a = 9.2;
   b = 3.7;
   c = 2;
   printf("%f / %d 的余数是 %lf\n", a, c, fmod(a,c));
   printf("%f / %f 的余数是 %lf\n", a, b, fmod(a,b));
   
   return(0);
}

9.200000 / 2 的余数是 1.200000
9.200000 / 3.700000 的余数是 1.800000

AC代码

#include<bits/stdc++.h>
using namespace std;
const double PI=acos(-1);
const double eps=1e-2;
struct Point
{
    double x,y;
} point[3];
double dist(struct Point a,struct Point b)
{
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
double area(double a,double b,double c)
{
    double p=(a+b+c)/2;
    return sqrt(p*(p-a)*(p-b)*(p-c));
}
double fgcd(double a,double b)
{
    if(b<eps) return a;
    else return fgcd(b,fmod(a,b));
}
int main()
{
    for(int i=0;i<3;i++) scanf("%lf%lf",&point[i].x,&point[i].y);
    double len[3];
    for(int i=0;i<3;i++) len[i]=dist(point[i],point[(i+1)%3]);
    double s=area(len[0],len[1],len[2]),r=(len[0]*len[1]*len[2])/(4*s);
    sort(len,len+3);
    double ang[3]={0};
    for(int i=0;i<2;i++)
    {
        ang[i]=2*asin(len[i]/(2*r));
    }
    ang[2]=2*PI-ang[0]-ang[1];
    double tp=fgcd(ang[0],fgcd(ang[1],ang[2]));
    double sx=(r*r*sin(tp))/2;
    double ans=sx*(2*PI/tp);
    printf("%.6lf",ans);
    return 0;
}