『模拟赛』暑假集训CSP提高模拟16

\(\color{skyblue}9-nine-\) 专场（

小阳历最水的一回。

日常RE挂分。

我这是不是风水不好？（逃）

9-nine-九次九日九重色

赛时以为是连续的...大样例模了半天没模懂...

按连续的思路打了个二分上去...还骗了30pts？(

官方题解

解释题解第一句话：

我们站在巨人的肩膀上可知：

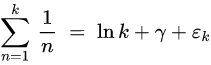
其中 \(\gamma\) 是欧拉-马歇罗尼常数(约等于\(0.577\))，而 \(\varepsilon_k\) 约等于 \(\frac{1}{2k}\)，并且随着 \(k\) 趋于正无穷而趋于 \(0\)。

稍微转换一下得到

\[\sum_{i=1}^n \frac{n}{i} =n\times( \ln n + \gamma + \varepsilon_k) \]

由于常数很小，可以忽略:

\[\sum_{i=1}^n \frac{n}{i} =n\ln n \approx n\log n \]

因此复杂度为 \(n \log n\)，可以暴力处理

按照官方题解打的Code，可以参考一下

int n,a[N],b[N],posb[N],posa[N],num[N];
vector<pair<int,int> > vec;

#define fi first
#define se second

bool cmp(pair<int,int> x,pair<int,int> y){
	if(x.fi==y.fi){
		return x.se>y.se;
	}else{
		return x.fi<y.fi;
	}
}

signed main(){
	n=rd;
	for(int i=1;i<=n;i++) a[i]=rd,posa[a[i]]=i;
	for(int i=1;i<=n;i++) b[i]=rd,posb[b[i]]=i;
	int cnt=0;
	vec.psb(mkp(-1,-1));
	for(int i=1;i<=n;i++){
		for(int j=1;i*j<=n;j++){
			vec.psb(mkp(posa[i],posb[i*j]));
			++cnt;
		}
	}
	sort(vec.begin(),vec.end(),cmp);
	
	num[1]=vec[1].se;
	int len=1;
	for(int i=2;i<=cnt;i++){
		if(vec[i].se>num[len]){
			num[++len]=vec[i].se;
		}else{
			int j=lower_bound(num+1,num+1+len,vec[i].se)-num;
			num[j]=vec[i].se;
		}
	}

	printf("%lld",len);
	return Elaina;
}

9-nine-天色天歌天籁音

守磨一下就会发现实际上是让求区间众数。

赛时打分块爆内存了，不愧是我先天RE圣体。

后来发现分块复杂度超了，遂改为莫队。

int n,m,maxn,len,ans[N],cnt[N],a[N],bl[N],sum[N];
struct Q{
	int l,r,id;
}q[N];
vector<int> lsh;
bool cmp(Q x,Q y){
	if(bl[x.l]==bl[y.l]){
		if(bl[x.l]&1) return x.r<y.r;
		else return x.r>y.r;
	}else return x.l<y.l;
}

void add(int x){
	sum[++cnt[a[x]]]++;
	if(cnt[a[x]]>maxn) maxn=cnt[a[x]];
	return;
}

void del(int x){
	if(sum[cnt[a[x]]]==1&&maxn==cnt[a[x]]) maxn--;
	sum[cnt[a[x]]--]--;
	return;
}

signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	
	n=rd,m=rd;
	len=sqrt(n);
	for(int i=1;i<=n;i++){
		a[i]=rd;
		lsh.psb(a[i]);
		bl[i]=(i-1)/len+1;
	}
	sort(lsh.begin(),lsh.end());
	lsh.erase(unique(lsh.begin(),lsh.end()),lsh.end());
	for(int i=1;i<=n;i++){
		a[i]=lower_bound(lsh.begin(),lsh.end(),a[i])-lsh.begin()-1;
	}
	
	for(int i=1;i<=m;i++){
		int l=rd,r=rd;
		q[i].l=l,q[i].r=r,q[i].id=i;
	}
	sort(q+1,q+1+m,cmp);
	
	int l=1,r=0;
	for(int i=1;i<=m;i++){
		while(l>q[i].l) add(--l);
		while(r<q[i].r) add(++r);
		while(r>q[i].r) del(r--);
		while(l<q[i].l) del(l++);
		ans[q[i].id]=-maxn;
	}
	for(int i=1;i<=m;i++) printf("%lld\n",ans[i]);
	return Elaina;
}

9-nine-春色春恋春熙风

显然一个串能重排形成是回文串当且仅当其字符数量均为偶数或者恰好有一个奇数

因为字符只有 \(22\) 种，所以我们可以考虑将其压缩称为一个状态 \(0\) 表示此字符为偶而 \(1\) 为奇

对于两条路之间的异或和:

\[\begin{aligned} dis(u,v) &= dis(u,1) \oplus dis(lca_{u,v},1) \oplus dis(v,1) \oplus dis(lca_{u,v},1) \\ &=dis(u,1) \oplus dis(v,1) \end{aligned}\]

于是有一条路径合法当且仅当\(dis_u\oplus dis_v\)为如下 \(23\) 种状态

\[000 \dots000 \]

\[100 \dots000 \]

\[\dots\dots \]

\[000 \dots010 \]

\[000 \dots001 \]

接下来暴力枚举点检查，对 \(2^22\) 种不同状态开一个桶记录下来。

每个桶都要维护最大的\(dep\)。

注意到一个点对u,vu,v对答案造成的贡献为\(dep_u+dep_v-2*dep_{lca}\)

于是考虑从某个点开始搜索，遍历其子树，检查桶内有没有合法的即可。

int n,cnt,idx,ll[N],rr[N],h[N],dep[N],siz[N],son[N];
int book[N*10],vis[N],ans[N],dis[N],id[N];
struct EDGE{
	int to,nxt,w;
}e[N];

void add(int x,int y,int w){
	e[++cnt]=(EDGE){y,h[x],w};
	h[x]=cnt;
}

void dfs(int x,int fa){
	siz[x]=1;
	ll[x]=++idx;
	dep[x]=dep[fa]+1;
	id[idx]=x;
	for(int i=h[x];i;i=e[i].nxt){
		int to=e[i].to;
		dis[to]=dis[x]^e[i].w;
		dfs(to,x);
		siz[x]+=siz[to];
		if(siz[son[x]]<siz[to]) son[x]=to;
	}
	rr[x]=idx;
}

void dfs2(int x,int keep){
	for(int i=h[x];i;i=e[i].nxt){
		int to=e[i].to;
		if(to==son[x]) continue;
		dfs2(to,0);
		ans[x]=max(ans[x],ans[to]);
	}
	if(son[x]){
		dfs2(son[x],1);
		ans[x]=max(ans[x],ans[son[x]]);
	}
	if(book[dis[x]]){
		ans[x]=max(ans[x],book[dis[x]]-dep[x]);
	}
	for(int i=0;i<=21;i++){
		if(book[dis[x]^(1<<i)]){
			ans[x]=max(ans[x],book[dis[x]^(1<<i)]-dep[x]);
		}
	}
	book[dis[x]]=max(dep[x],book[dis[x]]);
	for(int i=h[x];i;i=e[i].nxt){
		int to=e[i].to;
		if(to==son[x]) continue;
		for(int j=ll[to];j<=rr[to];j++){
			int k=id[j];
			if(book[dis[k]]){
				ans[x]=max(ans[x],book[dis[k]]+dep[k]-2*dep[x]);
			}
			for(int l=0;l<=21;l++){
				if(book[dis[k]^(1<<l)]){
					ans[x]=max(ans[x],book[dis[k]^(1<<l)]+dep[k]-2*dep[x]);
				}
			}
		}
		for(int j=ll[to];j<=rr[to];j++){
			book[dis[id[j]]]=max(book[dis[id[j]]],dep[id[j]]);
		}
	}
	if(!keep){
		for(int i=ll[x];i<=rr[x];i++){
			book[dis[id[i]]]=0;
		}
	}
}

signed main(){
	n=rd;
	int x;char ch;
	for(int i=2;i<=n;i++){
		x=rd,cin>>ch;
		add(x,i,1ll<<(ch-'a'));
	}
	dfs(1,1);
	dfs2(1,1);
	for(int i=1;i<=n;i++){
		printf("%lld ",ans[i]);
	}
	return Elaina;
}

9-nine-雪色雪花雪余痕

在改了 呜呜qwq

既然是9-nine专场，那挂张图吧