关于线段树优化建图
线段树优化建图
引入
对于这道板子题 但是我不会
大概意思就是：
有 \(n\) 个点、\(q\) 次操作。每一种操作为以下三种类型中的一种：
-
连一条 \(u→v\) 的有向边，权值为 w
-
对于所有 \(i∈[l,r]\) 连一条 \(u→i\) 的有向边，权值为 \(w\)
-
对于所有 \(i∈[l,r]\) 连一条 \(i→u\) 的有向边，权值为 \(w\)
求从点 \(s\) 到其他点的最短路。
\(1≤n,q≤10^5,1≤w≤10^9\)
——————————————华丽的分割线————————————
暴力 \(n^2\) 建边显然会爆时间，考虑优化。
考虑线段树优化建图。
线段树优化建图就是利用线段树，减少连边数量，从而降低复杂度。
过程
先种一颗线段树，并将所有叶子节点标号。
对于操作二，假设我们假设要假设...将 \(8\) 号节点向区间 \([3,7]\) 的所有点连权值为 \(w\) 的有向边
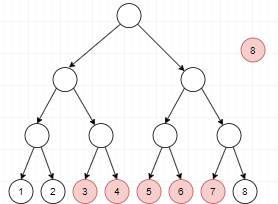
显然，可以向 \([3,4]\) 和 \([5,6]\) 的父亲节点分别连一条边，向 \(7\) 号节点连一条边，这样原本需要连 \(5\) 条边就被优化为连 \(3\) 条边。
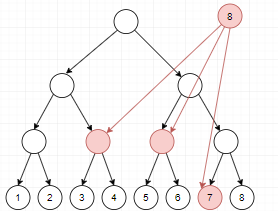
于是 \(O(n)\) 便优化为 \(O(\log n)\)。
那么对于操作三也可以用以上方法连边。
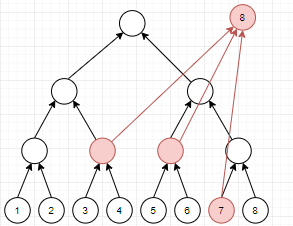
对于同时进行操作二和三，我们考虑建两颗线段树，一个只连自上而下（根节点到子节点）的边，我们称为出树；另一个只连自下而上（子节点到根节点）的边，成为入树
由于两棵树相同位置的叶子节点原本就是一个节点，所以要在它们相互之间连边权为 \(0\) 的边。
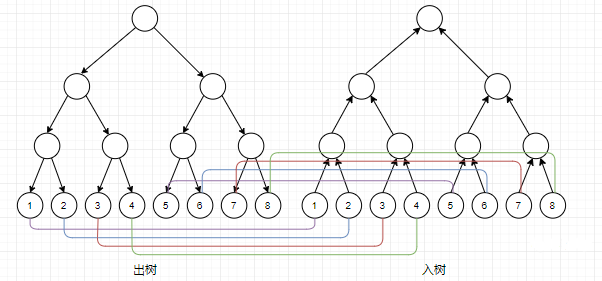
这样我们的树就建好了呢~
建树Code
void build(int rt,int l,int r){
if(l==r){
a[l]=rt;//记录编号
return;
}
int mid=(l+r)>>1;
add(rt,lson,0),add(rt,rson,0);//出树，根节点连子节点
add(lson+K,rt+K,0),add(rson+K,rt+K,0);//入树，子节点连根节点
build(lson,l,mid);
build(rson,mid+1,r);
}
//主函数中
build(1,1,n);
for(int i=1;i<=n;i++){
add(a[i],a[i]+K,0),add(a[i]+K,a[i],0);//两颗树之间原本相同的点连边
}
这里 \(K\) 是个常数（根据数据范围而定），酱紫像我们这些懒人就不用写两个建树代码了也可以用两个函数分别实现入树和出树的构建。
接下来就是连边了，用操作二举例就是酱紫
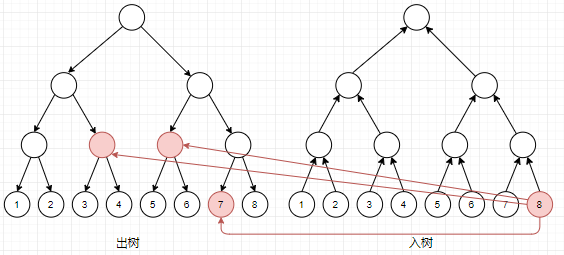
连边code
void modify(int rt,int l,int r,int ql,int qr,int v,int w){
if(l>=ql&&r<=qr){
if(op==2) add(v+K,rt,w);//入树的叶节点到出树的对应区间
else add(rt+K,v,w);//入树的对应区间到出树的叶节点
return;
}
int mid=(l+r)>>1;
if(ql<=mid) modify(lson,l,mid,ql,qr,v,w);
if(qr>mid) modify(rson,mid+1,r,ql,qr,v,w);
}
//主函数中
for(int i=1;i<=Q;i++){
cin>>op;
if(op==1){
cin>>v>>u>>w;
add(a[v]+K,a[u],w);//操作一就是将入树的叶子节点和出树的叶子节点连边
}else{
cin>>v>>l>>r>>w;
modify(1,1,n,l,r,a[v],w);
}
}
图建好啦~剩下的就是跑最短路
CODE
Elaina's Code
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define mkp make_pair
const int N=4e6+100;
const int inf=1e11;
const int K=1e6;
int hd[N],idx;
struct EDGE{
int nxt,to,w;
}e[N];
void add(int x,int y,int z){
e[++idx]={hd[x],y,z},hd[x]=idx;
}
int n,s,Q,dis[N],a[N];
bool vis[N];
priority_queue<pair<int,int> > q;
void dij(int x){
memset(dis,0x3f,sizeof(dis));
dis[x]=0;
q.push(mkp(0,x));
while(!q.empty()){
int k=q.top().second;
q.pop();
if(vis[k]) continue;
vis[k]=1;
for(int i=hd[k];i;i=e[i].nxt){
int to=e[i].to;
if(dis[to]>dis[k]+e[i].w){
dis[to]=dis[k]+e[i].w;
q.push(mkp(-dis[to],to));
}
}
}
}
#define lson (rt<<1)
#define rson (rt<<1|1)
void build(int rt,int l,int r){
if(l==r){
a[l]=rt;
return;
}
int mid=(l+r)>>1;
add(rt,lson,0),add(rt,rson,0);
add(lson+K,rt+K,0),add(rson+K,rt+K,0);
build(lson,l,mid);
build(rson,mid+1,r);
}
int op;
void modify(int rt,int l,int r,int ql,int qr,int v,int w){
if(l>=ql&&r<=qr){
if(op==2) add(v+K,rt,w);
else add(rt+K,v,w);
return;
}
int mid=(l+r)>>1;
if(ql<=mid) modify(lson,l,mid,ql,qr,v,w);
if(qr>mid) modify(rson,mid+1,r,ql,qr,v,w);
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>Q>>s;
build(1,1,n);
for(int i=1;i<=n;i++){
add(a[i],a[i]+K,0),add(a[i]+K,a[i],0);
}
int v,u,w,l,r;
for(int i=1;i<=Q;i++){
cin>>op;
if(op==1){
cin>>v>>u>>w;
add(a[v]+K,a[u],w);
}else{
cin>>v>>l>>r>>w;
modify(1,1,n,l,r,a[v],w);
}
}
dij(a[s]+K);
for(int i=1;i<=n;i++){
cout<<(dis[a[i]]==0x3f3f3f3f3f3f3f3fll?-1:dis[a[i]])<<' ';
}
return 0;
}
图自网搜，侵删。
