[BZOJ2720 Violet 5]列队春游（概率期望+组合数学）

合集 - 题解(*•ω•)(20)

1.数塔2024-02-162.[洛谷P2014] 选课2024-02-173.玉蟾宫 （悬线DP）2024-03-014.MooFest POJ-1990 （树状数组）2024-02-195.情书密码 （树状数组）2024-02-186.[SCOI 2009] 迷路 (矩阵快速幂)2024-03-137.[BZOJ3306] 树2024-03-188.[NOI2002] 荒岛野人2024-03-289.SHUFFLE 洗牌 (扩展欧几里得+龟速乘)2024-03-2910.[SDOI2009] Bill的挑战 (状压DP)2024-04-0911.P4168 [Violet] 蒲公英 (莫队的强制在线)2024-04-2212.P3667 [USACO17OPEN] Bovine Genomics G （set容器+二分）2024-04-2413.P7903 兜心の顶（构造）2024-05-12

14.[BZOJ2720 Violet 5]列队春游（概率期望+组合数学）2024-05-29

15.划分大理石(多重背包)2024-06-1416.P5746 [NOI2002] 机器人M号2024-06-2417.苍与红的试炼(数位DP)2024-06-2518.【唐赛】高一小学期22024-07-0819.P10779 BZOJ4316 小 C 的独立集 (仙人掌DP)2024-07-2420.关于求合法括号子序列个数2024-09-09

收起

阅读目录

• 列队春游

回到顶部

列队春游

问题描述

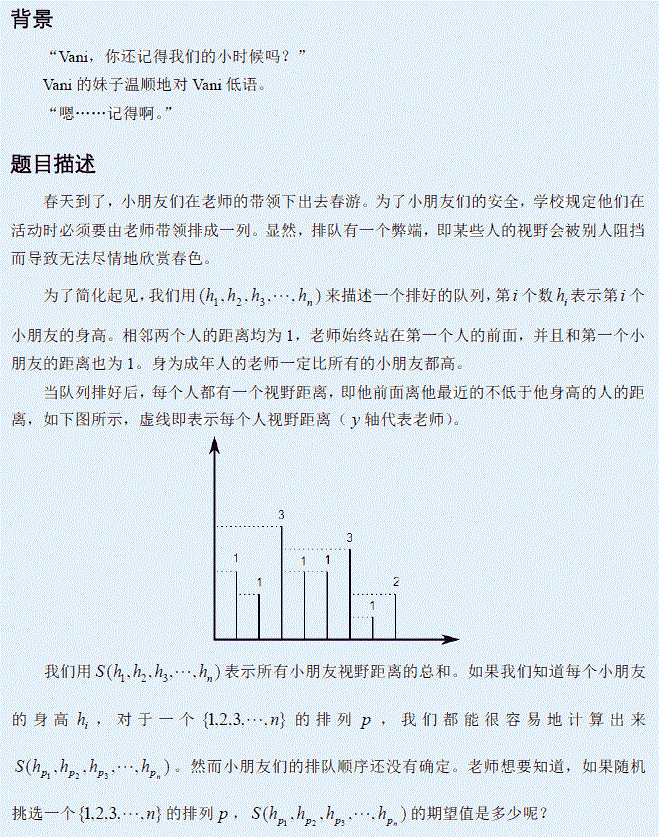
输入格式:

输出格式:

样例输入:

3
1 2 3

样例输出:

4.33

提示

思路

根据期望的线性性质，我们可以枚举每种可能的视野，然后求和

对于每种视野，其期望为该种视野的视野长度 * 该种视野的概率

设某个小朋友的视野期望为 $ans$ ,她的视野长度为 $L$

由于前面的第 $i$ 个人如果被看到就会对答案有 $1$ 的贡献，那么我们只要考虑前面的第 $i$ 个人会被看到的概率就可以了，可以直接求和

$$ans=\sum _{i=1}^{n}i\times P(L\ge i)$$

设不小于第$i$个小朋友身高的有$k$个人（不包括他自己）

那么会挡住小朋友的人包括自己随便放总共有 $A_n^{k+1}$ 种情况，其中那些会挡住小朋友的人不能放在小朋友前面的 $i-1$ 个位置，也不能放在小朋友的位置，所以方案数为 $A_{n-i}^k$ ,然后又因为小朋友自己有 $n-i+1$ 个位置可以放，所以乘上一个 $n-i+1$

所以最终

$$ans=\sum _{i=1}^n\frac{(n-i+1)A_{n-i}^k}{A_n^{k+1}}$$

然后就是 愉快的 导管子 导式子时光了

$$ans=\sum _{i=1}^n\frac{(n-i+1)\frac{(n-i)!}{(n-i-k)!}}{\frac{n!}{(n-k-1)!}}$$

$$ans=\frac{(n-k-1)!}{n!}\sum _{i=1}^n\frac{(n-i+1)!}{(n-i-k)!}$$

$$ans=\frac{(n-k-1)!}{n!}(k+1)!\sum _{i=1}^n\frac{(n-i+1)!}{(n-i-k)!(k+1)!}$$

$$ans=\frac{(n-k-1)!}{n!}(k+1)!\sum _{i=1}^n{C}_{n-i+1}^{k+1}$$

$$ans=\frac{(n-k-1)!}{n!}(k+1)!C_{n+1}^{k+2}$$

$$ans=\frac{n+1}{k+2}$$

很多题解都没有解释倒数第二个式子是怎么导出来的（可能只有我这个蒟蒻看不懂吧 大悲）
简单解释一下：
先将 $\sum$ 展开一下，得到

$$ans=\frac{(n-k-1)!}{n!}(k+1)!(C_{n-1+1}^{k+1}+C_{n-2+1}^{k+1}+...+C_2^{k+1}+C_1^{k+1})$$

在式子最后加上一个 $C_1^{k+2}$ (由定义可知$C_1^{k+2}=0$），得

$$ans=\frac{(n-k-1)!}{n!}(k+1)!(C_{n-1+1}^{k+1}+C_{n-2+1}^{k+1}+...+C_2^{k+1}+C_1^{k+1}+C_1^{k+2})$$

由组合数递推式子 $C_n^m=C_{n-1}^{m-1}+C_{n-1}^m$ 将最后两项合并可得

$$ans=\frac{(n-k-1)!}{n!}(k+1)!(C_{n-1+1}^{k+1}+C_{n-2+1}^{k+1}+...+C_2^{k+1}+C_2^{k+2})$$

反复合并，最终得到

$$ans=\frac{(n-k-1)!}{n!}(k+1)!C_{n+1}^{k+2}$$

code

Elaina's code

#include<bits/stdc++.h>
using namespace std;
const double eps=1e-8;
const int N=5050;
#define int long long
#define inf 0x3f
#define INF 0x3f3f3f3f
#define mst(a,b) memset(a,b,sizeof(a))
#define re register
#define Elaina 0
#define lson (rt<<1)
#define rson (rt<<1|1)
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
    for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
    return x*f;
}

int n,a[N];
double h[N],ans=0,sum=0;

main(){
	n=read();
	for(int i=1;i<=n;i++){
		a[i]=read();
		h[a[i]]++;
	}
	
	for(int i=1;i<=1000;i++){
		ans+=1.0*h[i]*(n+1)/(n-sum+1);
		sum+=h[i];
	}
	printf("%.2lf",ans);
    return Elaina;
}

都看到这了，真的不点个赞吗(>ω<*)