关于二分图
二分图
定义
二分图，又称二部图，英文名叫 \(Bipartite graph\)
二分图是 节点由两个集合组成，且两个集合内部没有边的图
换言之，存在一种方案，将节点划分成满足以上性质的两个集合
举个栗子（免责声明：本人并无种族歧视）
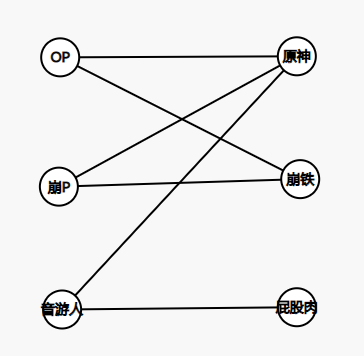
谁说OP不能玩崩铁
性质
- 如果两个集合中的点分别染成黑色和白色，可以发现二分图中的每一条边都一定是连接一个黑色点和一个白色点。
- 二分图不存在长度为奇数的环 （因为每条边都是从一个集合到另一个集合，如果要回到一个集合那只能走偶数次）
二分图的判定
就像数学一样，我们可以通过二分图的性质判定二分图
由性质1我们可以用染色法进行二分图的判定，尝试用黑白两种颜色标记图中的节点：当一个节点被标记后，它的所有相邻节点应该被标记与它相反的颜色。若标记过程中产生冲突，则说明图在存在奇环。用 \(DFS\) 或 \(BFS\) 均可，多数用 \(DFS\) 因为好打，时间复杂度为 \(O(N+M)\)
CODE
Elaina's code
#include<bits/stdc++.h>
using namespace std;
const int N=500100;
#define int long long
#define inf 0x3f
#define INF 0x7fffffffffffffff
#define mst(a,b) memset(a,b,sizeof(a))
#define re register
#define Elaina 0
inline int read(){
int x=0,f=1;
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
return x*f;
}
int n,m,head[N*2],idx,col[N],ans;
int a[N],b[N],c[N];
struct EDGE{
int to,nxt,w;
}e[N*2];
void add(int x,int y,int z){
e[++idx].to=y;
e[idx].nxt=head[x];
e[idx].w=z;
head[x]=idx;
}
bool dfs(int x,int fa,int co){
col[x]=co;
for(int i=head[x];~i;i=e[i].nxt){
int to=e[i].to;
if(to!=fa){
if(!col[to]&&!dfs(to,x,3-co)) return 0;
if(col[to]==co) return 0;
}
}
return 1;
}
main(){
//省略输入
//……………………………………
bool flag=1;
for(int i=1;i<=n;i++){
if(col[i]==0){
col[i]=1;
if(!dfs(i,0,1)){
flag=0;
break;
}
}
}
if (flag) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
return Elaina;
}
二分图的应用
匹配
在图论中，假设图 \(G=(V,E)\)，其中 \(V\) 是点集，\(E\) 是边集
-
一组两两没有公共点的边集 \(M(M\in E)\) 称为这张图的 匹配
-
定义匹配的大小为其中边的数量 \(|M|\)，其中边数最大的 \(M\) 为 最大匹配
-
当图中的边带权的时候，边权和最大的为 最大权匹配
-
匹配中的边称为 匹配边，反之称为 未匹配边
-
一个点如果属于 \(M\) 且为至多一条边的端点，称为 匹配点，反之称为 未匹配点
-
交错路（alternating path）始于非匹配点且由匹配边与非匹配边交错而成
-
增广路（augmenting path）是始于非匹配点且终于非匹配点（除了起始的点）的交错路。增广路中边的数量是奇数
二分图的最大匹配
匈牙利算法
流程
- 设匹配 \(M\) 是空集，即所有边都是非匹配边
- 寻找增广路 \(path\) ，把路径上所有边的匹配状态取反，得到一个更大的匹配 \(M\)
- 重复第 \(2\) 步，直至图中不存在增广路。
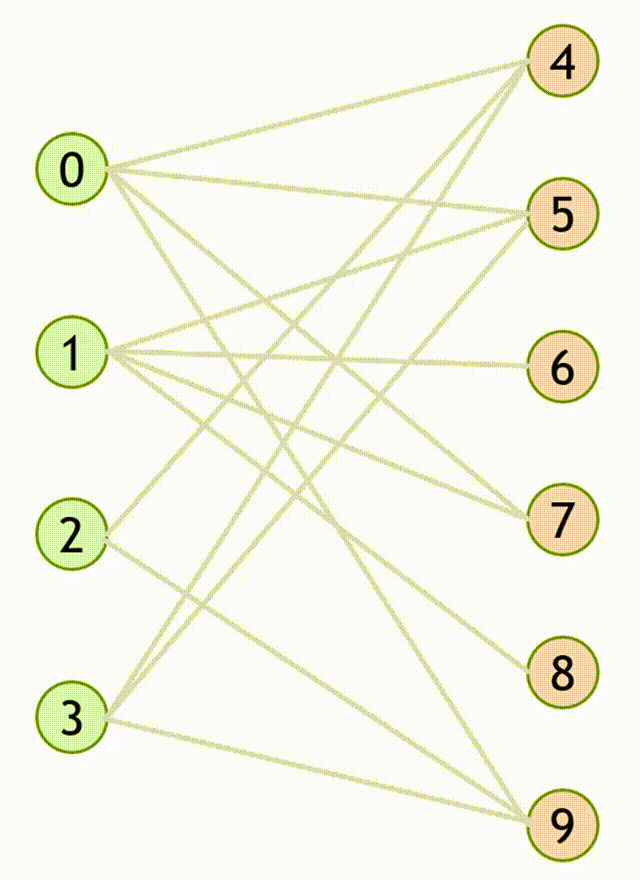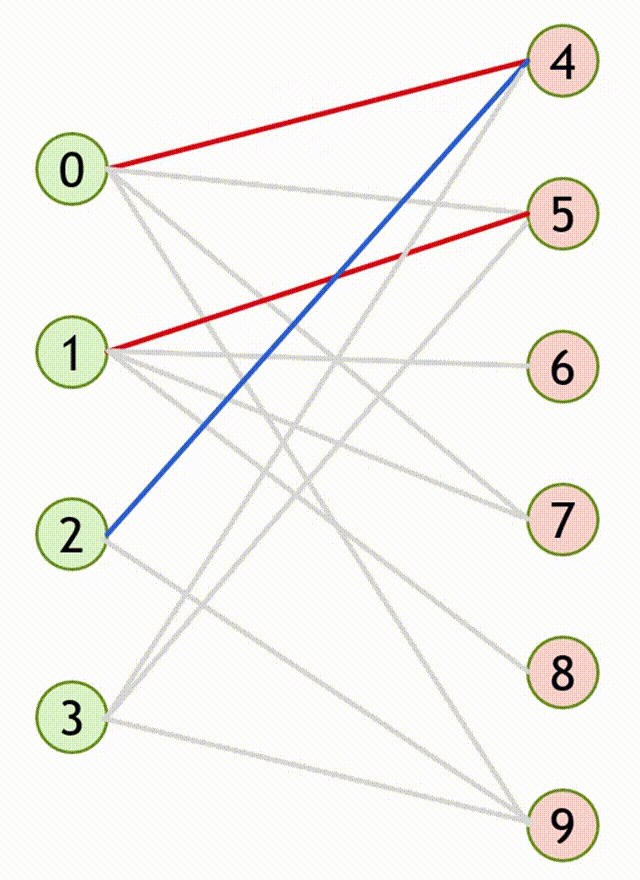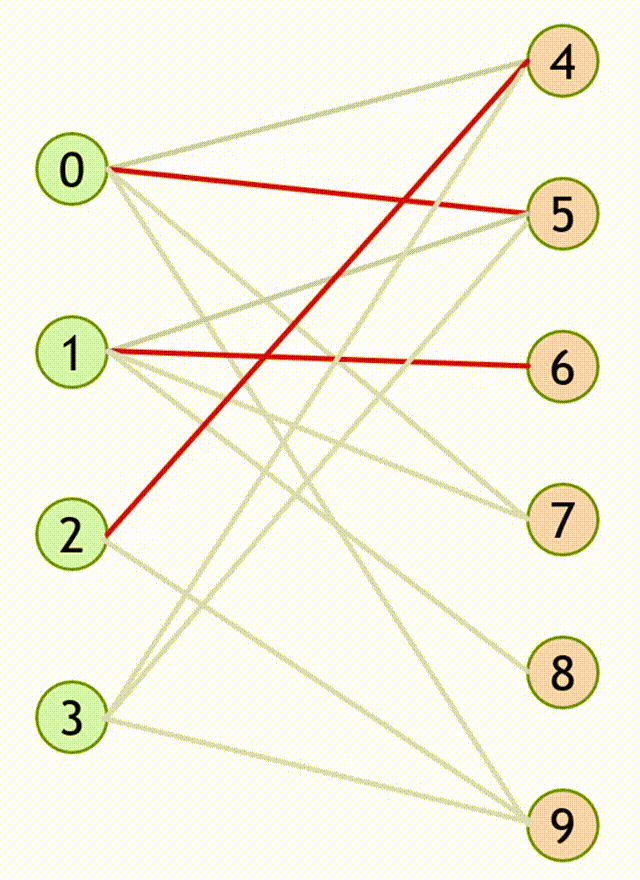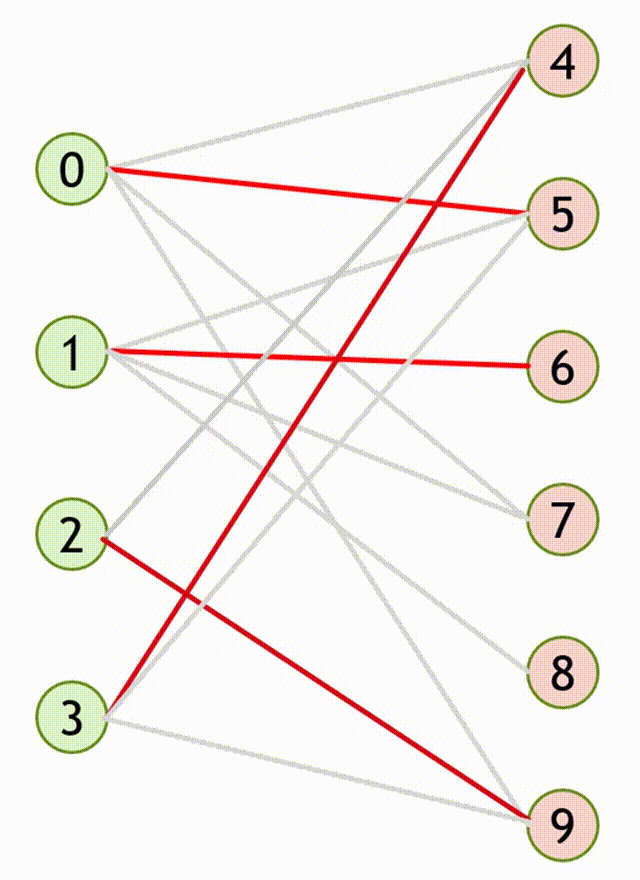
CODE
Elaina's code
#include<bits/stdc++.h>
using namespace std;
const int N=10005;
#define int long long
#define inf 0x3f
#define INF 0x3f3f3f3f
#define mst(a,b) memset(a,b,sizeof(a))
#define Elaina 0
inline int read(){
int x=0,f=1;
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
return x*f;
}
int n,m,head[N],idx,match[N],ans;
int vis[N];
struct EDGE{
int to,nxt,w;
}e[N*2];
void add(int x,int y){
e[++idx].to=y;
e[idx].nxt=head[x];
head[x]=idx;
}
int xyl(int x){
for(int i=head[x];~i;i=e[i].nxt){
int to=e[i].to;
if(!vis[to]){
vis[to]=1;
if(!match[to]||xyl(match[to])){
match[to]=x;
return 1;
}
}
}
return 0;
}
main(){
mst(head,-1);
n=read(),m=read();
for(int i=1;i<=m;i++){
int x=read(),y=read();
add(x,y+n);
}
for(int i=1;i<=n;i++){
mst(vis,0);
if(xyl(i)){
ans++;
}
}
printf("%lld\n",ans);
return Elaina;
}
二分图最小点覆盖（König 定理）
最小点覆盖：选最少的点，满足每条边至少有一个端点被选。
二分图中，最小点覆盖 \(=\) 最大匹配。
应用
-
每个选择都有两种条件
-
两种条件至少选择一个时，选择成立
-
要求全部选择成立，求最少满足条件总数
例题
Asteroids 穿越小行星群
二分图最大独立集
最大独立集：选最多的点，满足两两之间没有边相连。
因为在最小点覆盖中，任意一条边都被至少选了一个顶点，所以对于其点集的补集，任意一条边都被至多选了一个顶点，所以不存在边连接两个点集中的点，且该点集最大。
因此二分图中，最大独立集 \(=n-\) 最小点覆盖
应用
-
寻找冲突
-
对冲突的对象连边
例题
猫和狗
