动态规划之区间DP
定义
区间DP也叫合并类DP
合并 意思就是将两个或多个部分进行整合，当然也可以反过来，也就是是将一个问题进行分解成两个或多个部分
特点：
能将问题分解为两两合并的形式
一般思路：
对整个问题设最优值，枚举合并点，将问题分解成为左右两个部分，最后将左右两个部分的最优值进行合并得到原问题的最优值。
例题
合并石子
描述
传送门
在一个圆形操场的四周摆放着n堆石子。现要将石子有次序地合并成一堆。规定每次只能选相邻的2 堆石子合并成新的一堆，并将新的一堆石子数记为该次合并的得分。
试设计一个算法。
选择一种合并石子的方案，使得做 n-1 次合并得分总和最大。
选择一种合并石子的方案，使得做 n−1 次合并得分总和最小。
对于给定n堆石子,计算合并成一堆的最小得分和最大得分。
思路
问题不具有局部最优代替整体最优，不能用贪心法
举个例子
N=6
贪心:
第一次合并5 4 6 5 4 得分+5
第二次合并9 6 5 4 得分+9
第三次合并9 6 9 得分+9
第四次合并15 9 得分+15
第五次合并24 得分+24
共计62分
最优：
第一次合并7 6 5 4 2 得分+7
第二次合并13 5 4 2 得分+13
第三次合并13 5 6 得分+6
第四次合并13 11 得分+11
第五次合并24 得分+24
共计61分
但是可以拆分为多个子问题，再对其进行合并
设a[i][j]表示从第i堆到第j堆石子数总和
dp[i][j]表示将从第i堆石子合并到第j堆石子的最大得分
g[i][j]表示将从第i堆石子合并到第j堆石子的最小得分
由题意得
dp[i][j]=max(dp[i][j],dp[i][k]+dp[k+l][j]+a[i][j])
g[i][j]=min(g[i][j],g[i][k]+g[k+l][j]+a[i][j])
dp[i][i]=0 g[i][i]=0
因为我们是要求一个任意区间的和（a[i][j]）因此我们可以用前缀和优化一下
code
code
#include<bits/stdc++.h>
using namespace std;
#define Elaina 0
const int N=2010
int sum,n,m,dp[N][N],g[N][N],a[N],s[N];
void DP(){
for(int len=2;len<=n;len++){
for(int i=1;i+len-1<=2*n;i++){
int j=i+len-1;
for(int k=i;k<j;k++){
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+s[j]-s[i-1]);
g[i][j]=max(g[i][j],g[i][k]+g[k+1][j]+s[j]-s[i-1]);
}
}
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
a[n+i]=a[i];
}
for(int i=1; i<=n*2; i++){//前缀和预处理
s[i]=s[i-1]+a[i];
}
memset(dp,0x3f,sizeof(dp));
for(int i=1;i<=2*n;i++){
dp[i][i]=0;
}
DP();
int ans1=INF,ans2=0;
for(int i=1;i<=n;i++){
ans1=min(dp[i][n+i-1],ans1);
ans2=max(g[i][n+i-1],ans2);
}
cout<<ans1<<endl<<ans2<<endl;
return Elaina;
}
思路
设dp[i][j]表示这个数前i位分成j段得到的最大乘积
易得
dp[i][j]=dp[k-1][j-1]*a[k][i]
想要输出划分方式只需记录决策点即可
code
code
#include<bits/stdc++.h>
using namespace std;
#define N 1010
#define ll long long
#define INF 0x3f3f3f3f
#define inf 0x3f
#define Elaina 0
ll ink,n,m,T,a[N][N],dp[N][N],path[N][N];
char ss[50];
void bag(){
for(ll i=1; i<=n; i++){
int ki=min(i,m);
for(int j=1;j<=ki;j++){
for(int k=1;k<=i;k++){
if(dp[k-1][j-1]*a[k][i]>dp[i][j]){
dp[i][j]=dp[k-1][j-1]*a[k][i];
path[i][j]=k-1;
}
}
}
}
}
void backtrack(int n,int m){
if(!m){
return;
}
backtrack(path[n][m],m-1);
for(int i=path[n][m]+1;i<=n;i++){
cout<<ss[i];
}
cout<<" ";
return ;
}
int main(){
cin>>T;
while(T--){
memset(path,0,sizeof(path));
memset(dp,0,sizeof(dp));
memset(ss,0,sizeof(ss));
memset(a,0,sizeof(a));
cin>>ss+1;
n=strlen(ss+1);
cin>>m;
for(int i=1;i<=n;i++){
ink=0;
for(int j=i;j<=n;j++){
ink=ink*10+ss[j]-'0';
a[i][j]=ink;
}
}
dp[0][0]=1;
bag();
cout<<dp[n][m]<<endl;
if(m==n){
for(int i=1;i<=n;i++){
cout<<ss[i]<<" ";
}
}else{
backtrack(n,m);
}
cout<<endl;
}
return Elaina;
}
凸多边形的三角剖分
描述
给定一具有N个顶点（从1到N编号）的凸多边形，每个顶点的权均已知。问如何把这个凸多边形划分成N-2个互不相交的三角形，使得这些三角形顶点的权的乘积之和最小？
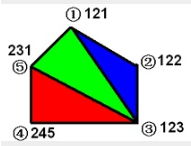
思路
按顺时针将顶点编号，设dp[i][j]表示i~j这一段连续顶点的多边形划分后的最小乘积（最优解），枚举点k,i,j相连成三角形，并把原多边形划分成两个子多边形，易得
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]+a[i]*a[j]*a[k])
code
code
#include<bits/stdc++.h>
using namespace std;
#define N 2010
#define ll long long
#define INF 0x3f3f3f3f
#define inf 0x3f
#define Elaina 0
ll dp[N][N],a[N],n,k;
void DP(){
for(int len=2;len<n;len++){
for(int i=1;i<=n-len;i++){
int j=i+len;
for(int k=i+1;k<j;k++){
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]+a[i]*a[k]*a[j]);
}
}
}
}
int main(){
cin>>n;
memset(dp,inf,sizeof(dp));
for(int i=1;i<=n;i++){
cin>>a[i];
dp[i][i+1]=0;
}
DP();
cout<<dp[1][n];
return Elaina;
}
