动态规划之线性DP

概念

具有线性阶段划分的动态规划算法叫作线性动态规划（简称线性DP）。若状态包含多个维度，则每个维度都是线性划分的阶段，也属于线性DP，如下图所示：

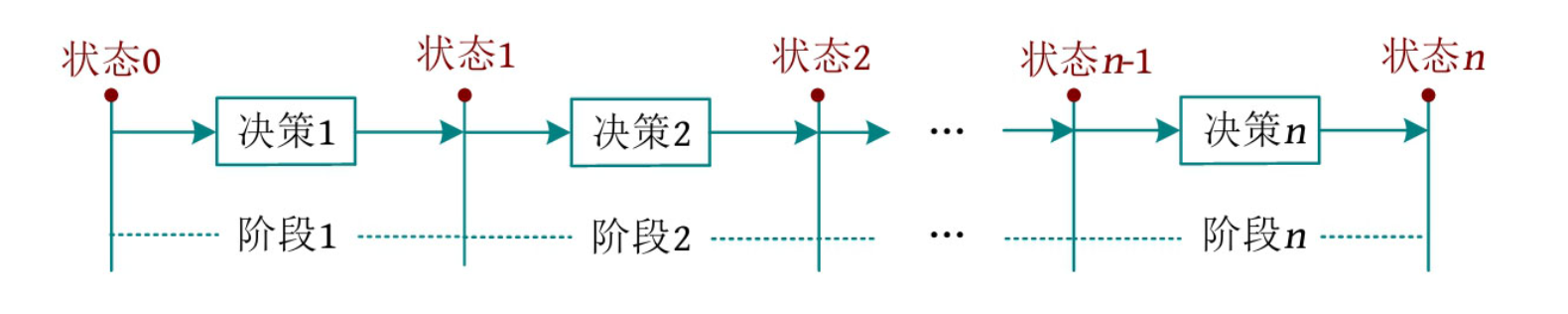
如果状态包含多个维度，但是每个维度上都是线性划分的阶段，也属于线性 DP。比如背包问题、区间 DP、数位 DP 等都属于线性 DP。

例题

求最长上升序列（LIS）

描述：

设有由n个不相同的整数组成的数列，记为:b(1)、b(2)、……、b(n)且b(i)<>b(j) (i<>j)，若存在i1<i2<i3< … < ie 且有b(i1)<b(i2)< … <b(ie)则称为长度为e的不下降序列。程序要求，当原数列出之后，求出最长的上升序列。
例如13，7，9，16，38，24，37，18，44，19，21，22，63，15。例中13，16，18，19，21，22，63就是一个长度为7的不下降序列，同时也有7 ，9，16，18，19，21，22，63长度为8的不下降序列。

思路：

设dp[i]表示以第i个数结尾的所有子序列集合，则dp[i]为最大子序列长度
枚举第i个数前面的数j，如果a[j]<a[i]说明a[j]可能是以a[i]为结尾的最长子序列的倒数第二个数，则用dp[j]+1更新dp[i]
由此可得状态转移方程为
dp[i]=max(f[i],f[j]+1)

code

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define N 1010000
#define Elaina 0
int n,te,a[N],dp[N],g[N],path[N],ans=0;
void DP(){
	for(int i=1;i<=n;i++){
		dp[i]=1;
		for(int j=0;j<=i;j++){
			if(a[i]>a[j]&&dp[i]<dp[j]+1){
				dp[i]=dp[j]+1;
				path[i]=j;//保存路径 
				if(ans<dp[i]){
					ans=dp[i];
					te=i;
				}
			}
		}
	}
}
void backtrack(int x){
	if(x==0){
		return;
	}
	backtrack(path[x]);
	cout<<a[x]<<" ";
	return ;
}
int main(){
	n=0;
	int x;
	while(cin>>x){
		a[++n]=x;
	}
	DP();
	cout<<"max="<<ans<<endl;
	backtrack(te);
	return Elaina;
}

变形:

友好城市

最长公共子串长度（LCS）

描述：

信息学小组截获了两个序列,序列A和B,规定两个序列所隐藏的信息就是两者的最长公共子串(注意,这里的子串是指连续的,比如说212325233中212是212325233的子串,而213或者223都不是212325233的子串),现在,他们将这个任务交给你,你要找出这两个序列所隐藏信息的长度

思路：

一个数列 S，如果分别是两个或多个已知数列的子序列，且是所有符合此条件序列
中最长的，则S 称为已知序列的最长公共子序列。
LCS问题的分支：最长公共子串与最长公共子序列
子串（Substring）是串的一个连续的部分，子序列（Subsequence）则是从不改变序
列的顺序，而从序列中去掉任意的元素而获得的新序列；更简略地说，前者（子串）
的字符的位置必须连续，后者（子序列LCS）则不必。比如字符串acdfg同akdfc的最
长公共子串为df，而他们的最长公共子序列是adf

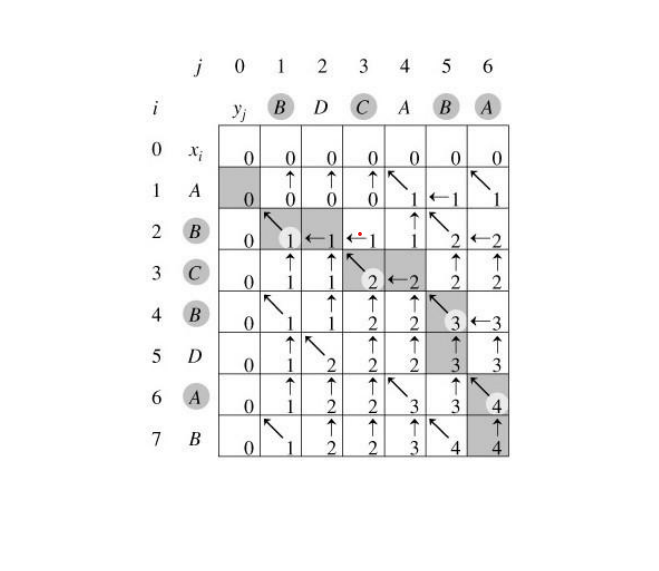
由图易得
当i=0 ro j=0时
dp[i][j]=0

当i,j>0且Xi=Yj时
dp[i][j]=dp[i-1][j-1]+1

当i,j>0且Xi!=Yj时
dp[i][j]=max(dp[i][j-1],dp[i-1][j])

code

code

#include<bits/stdc++.h>
using namespace std;
#define N 1010
#define Elaina 0
#define mst(a,b) memset(a,b,sizeof(a))
int ans,dp[N][N];
char a[N],b[N];
int main(){
	mst(dp,0);
	int i=1,j=1;
	cin>>a+1>>b+1;
	int n=strlen(a+1),m=strlen(b+1);
	for(i=1;i<=n;i++){
    	for(j=1;j<=m;j++){
    		if(a[i]==b[j]){
    			dp[i][j]=dp[i-1][j-1]+1;
    			ans=max(ans,dp[i][j]);
			}else{
				dp[i][j]=0;
			}
		}
	}
	cout<<ans;
	return Elaina;
}