【洛谷P1962】矩阵快速幂求Fibonacii数列

题目描述
求出斐波那契数列第n项 ： Fn mod 10^9 + 7 的值。

输入格式
一行一个正整数 n

输出格式
一行一个整数表示答案

【数据范围】
对于 %60% 的数据，1≤n≤92
对于 %100% 的数据，1≤n<2^63

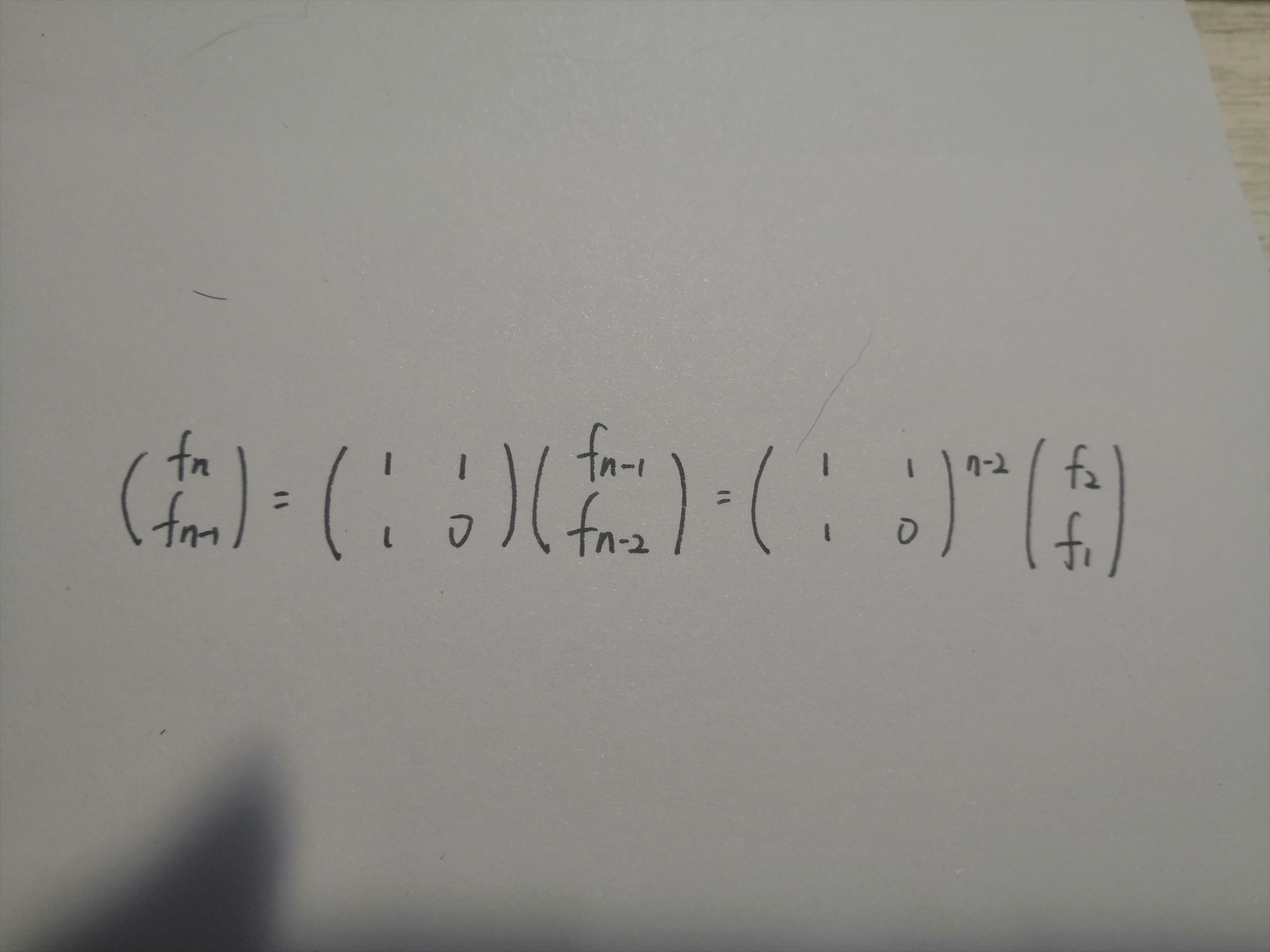
#include<cstdio>
using namespace std;

const long long mo = 1000000007;
long long f[3][3];
long long a[3];

void mul1() {
	long long c[3] = {0};
	for (int i = 1; i <= 2; i++)
		for (int k = 1; k <= 2; k++) 
			c[i] = (c[i] + (f[i][k] * a[k]) % mo) % mo;
	for (int i = 1; i <= 2; i++) a[i] = c[i] % mo;
}

void mul2() {
	long long c[3][3] = {0};
	for (int i = 1; i <= 2; i++)
		for (int j = 1; j <= 2; j++)
			for (int k = 1; k <= 2; k++)
				c[i][j] = (c[i][j] + (f[i][k] * f[k][j]) % mo) % mo;
	for (int i = 1; i <= 2; i++)
		for (int j = 1; j <= 2; j++)
			f[i][j] = c[i][j] % mo;
}

int main() {
	long long n;
	scanf("%ld", &n);
	a[1] = 1; a[2] = 1; 
	f[1][1] = f[1][2] = f[2][1] = 1; f[2][2] = 0;
	n -= 2;
	while (n > 0) {
		if (n & 1) mul1();
		n = n >> 1;
		mul2();
	}
	printf("%ld\n", a[1]);
        return 0;
}