【笔记】关于位运算

位运算是在二进制的基础上所运行的

主要分为六种运算符：

一、&（按位与）：

1、概念：

若有 a & b = c

将 a 和 b 转换为二进制，并将其每二进制位一 一对应

若相同位数均为 1 时， c 中对应位数为 1；

否则为 0 。

2、例子：

若存在 9 & 5

9 的二进制为（00 001 001），5的二进制为（00 000 101）

那么 9 & 5 = 1（00 000 001）

3、图解：

 

 

二、|（按位或）：

1、概念：

若有 a | b = c

将 a 和 b 转换为二进制，并将其每二进制位一 一对应

若相同位数只要有至少一个 1 时， c 中对应位数为 1；

否则为 0 。

2、例子：

若存在 9 | 5

9 的二进制为（00 001 001），5的二进制为（00 000 101）

那么 9 | 5 = 13（ 00 001 101）

3、图解：

 

三、^（按位异或）：

1、概念：

若有 a ^ b = c

将 a 和 b 转换为二进制，并将其每二进制位一 一对应

若相同位数上的数字不相同时， c 中对应位数为 1；

否则为 0 。

2、例子：

若存在 9 ^ 5

9 的二进制为（00 001 001），5的二进制为（00 000 101）

那么 9 ^ 5 = 12（ 00 001 100）

3、图解：

 

 

四、~（取反）：

1、概念：

若有 ~ a = b

将 a 转换为二进制

并将其每二进制上的数字转换， 0 转换成 1；

1 转换成 0，存到 b 中一 一对应 。

2、例子：

若存在 ~ 9

9 的二进制为（00 001 001）

那么 ~ 9 = 246（ 11 110 110）

3、图解：

 

 

五、<<（左移）：

1、概念：

若有 a << b = c

将 a 转换为二进制

并将其每二进制上的数字向左移 b 位， 高位丢弃；

低位补 0 ，存到 c 中一 一对应。

2、例子：

若存在 9 << 5

9 的二进制为（00 001 001）

那么 9 << 5 = 32（00 100 000）

3、图解：

 

 

 

 （每一位向左移 5 位）

六、>>（右移）：

1、概念：

若有 a >> b = c

将 a 转换为二进制

并将其每二进制上的数字向右移 b 位， 高位补 0；

低位丢弃 ，存到 c 中一 一对应。

2、例子：

若存在 9 >> 3

9 的二进制为（00 001 001）

那么 9 >> 3 = 1（00 000 001）

3、图解：

 

 （每一位向右移3位）

PS：

1、对于有符号数（比如负数），在右移时，符号将一起移动。

2、当被右移运算的有符号数是正数时，最高位补 0，为负数时，最高位补 1 。

位运算的一些有用知识：

下面是由江苏省淮阴中学薛志坚整理的一些常见操作:（来源于一个dalao的博客）

 

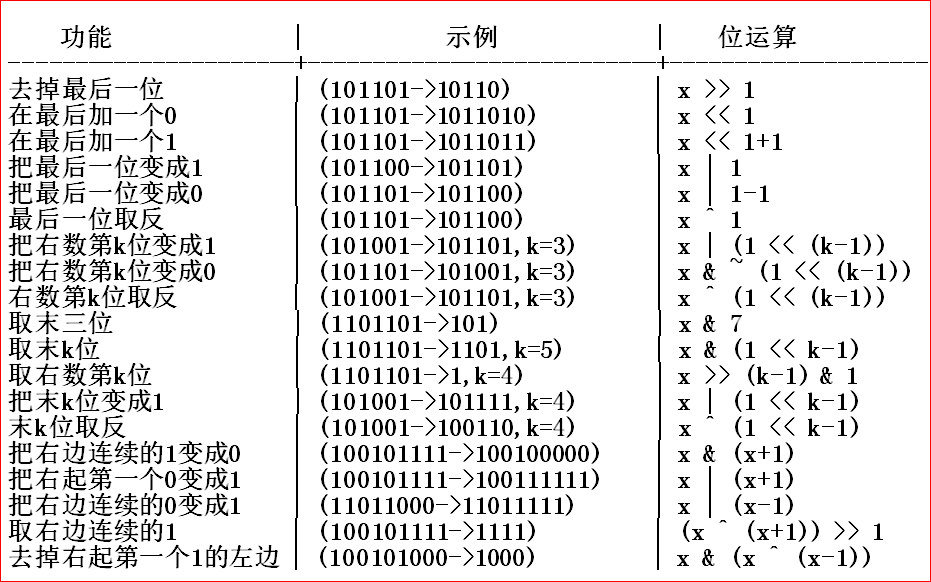
 窝 jiao 得很有用，整理下来用博客存上

再加一条：

求 lowbit：n & -n（树状数组）

来自深受 dp 毒害的瑟瑟发抖的小可怜的控诉

我讨厌 dp