Jamie and Interesting Graph
Problem
题目大意
构造一个n点m边的带权简单连通图G,要求点1到点n的最短路径与G的最小生成树权值都为质数。其中n范围为[2, 105],边权范围为[1, 109]。
算法
特判n == 2的情况,否则使最短路径和最小生成树权值为2和100003。
点1与点n连权值为2的边。
点2与点n连权值为100004 – n的边。
点3到点n – 1与点n连权值为1的边。
在不重边不自环的前提下,将剩下的边数用完,权值相对设得大些即可,
时间复杂度:
O(m)
空间复杂度:
O(1)
代码
1 def doit(n, m):
2 if (n == 2):
3 print(2, 2)
4 print(1, 2, 2)
5 return
6 sp = 2
7 mstw = 100003
8 print(sp, mstw)
9 print(1, n, sp)
10 print(2, n, mstw - n + 3 - sp)
11 for i in range(3, n):
12 print(i, n, 1)
13 for i in range(2, n):
14 for j in range(1, i):
15 if (m == n - 1):
16 return
17 print(i, j, mstw)
18 m -= 1
19
20 n, m = input().split()
21 doit(int(n), int(m))

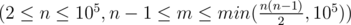 — the required number of vertices and edges.
— the required number of vertices and edges.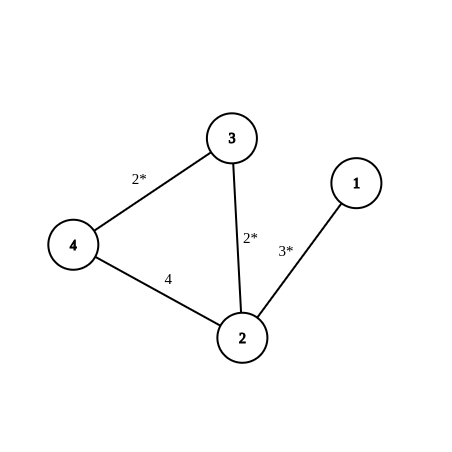 Shortest path sequence:
Shortest path sequence: 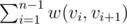 is minimized where
is minimized where 
 浙公网安备 33010602011771号
浙公网安备 33010602011771号