简单易懂地从底至上地学懂CuTe

背景补充

为什么要加速MMA? 为什么要引入tensor core? 为什么要对tensor级别数据进行操作?
tensor core的底层电路可能性分析:https://www.youtube.com/watch?v=xjjN9q2ym6s
tensor core 优化手段: https://bruce-lee-ly.medium.com/nvidia-tensor-core-cuda-hgemm-advanced-optimization-5a17eb77dd85
具体分析可以自行观看; 笔者这里先做一个简单的分析:

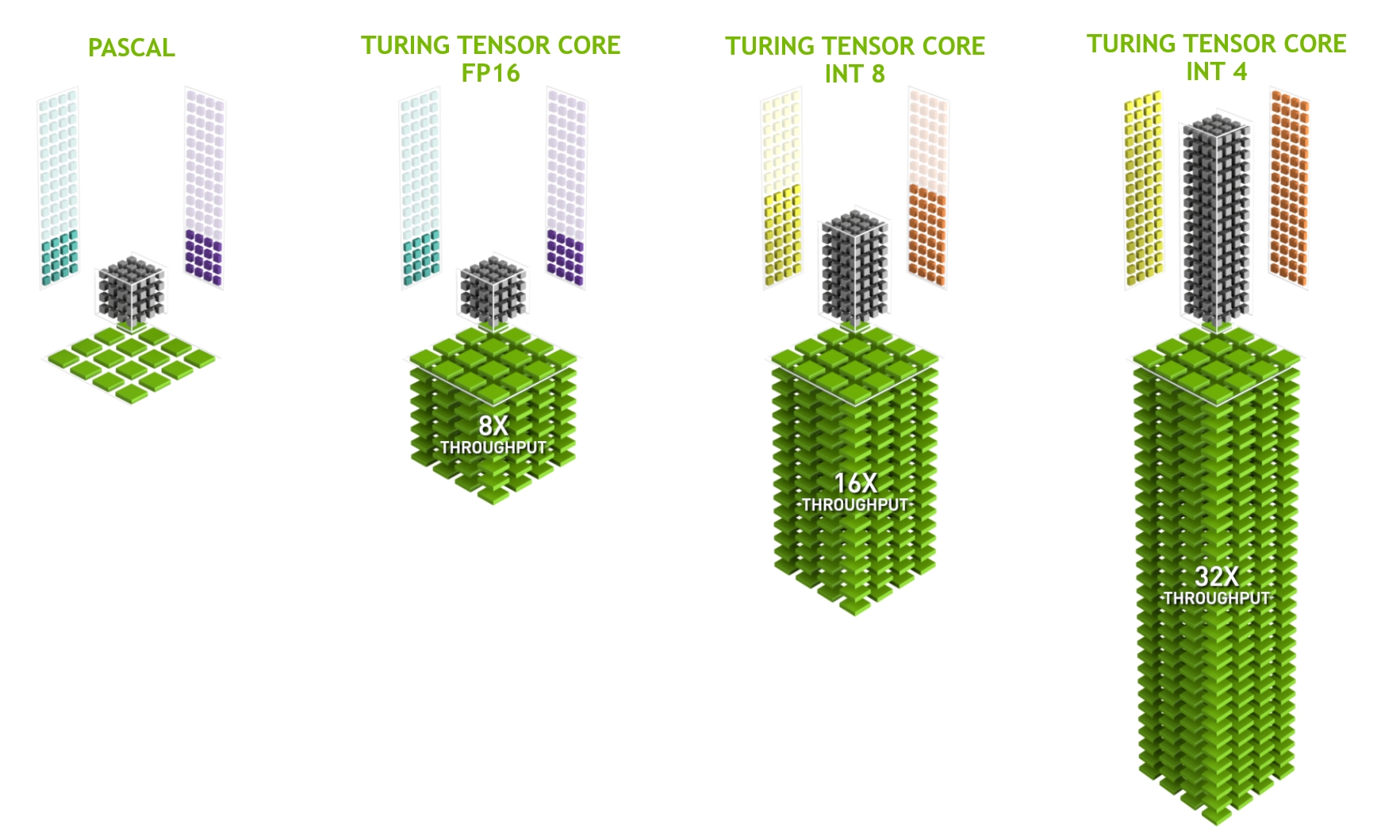
就以上面的两种架构进行比对:

根据NV官方信息, tensorcore能比cuda core 有8倍的吞吐量提升, 这是为什么呢?
因为TC特殊硬件的引入, 一个小矩阵的乘加操作可以简化为一个三级流水, 即mul -> add1 -> add2 , 这样如果三级流水打满, 理论上是可以一个cycle出一个结果的. 接下来笔者会仔细计算一遍为什么会有8倍的提升, 我们会以SM为单位进行分析:

  				上图是pascal架构下的一个SM

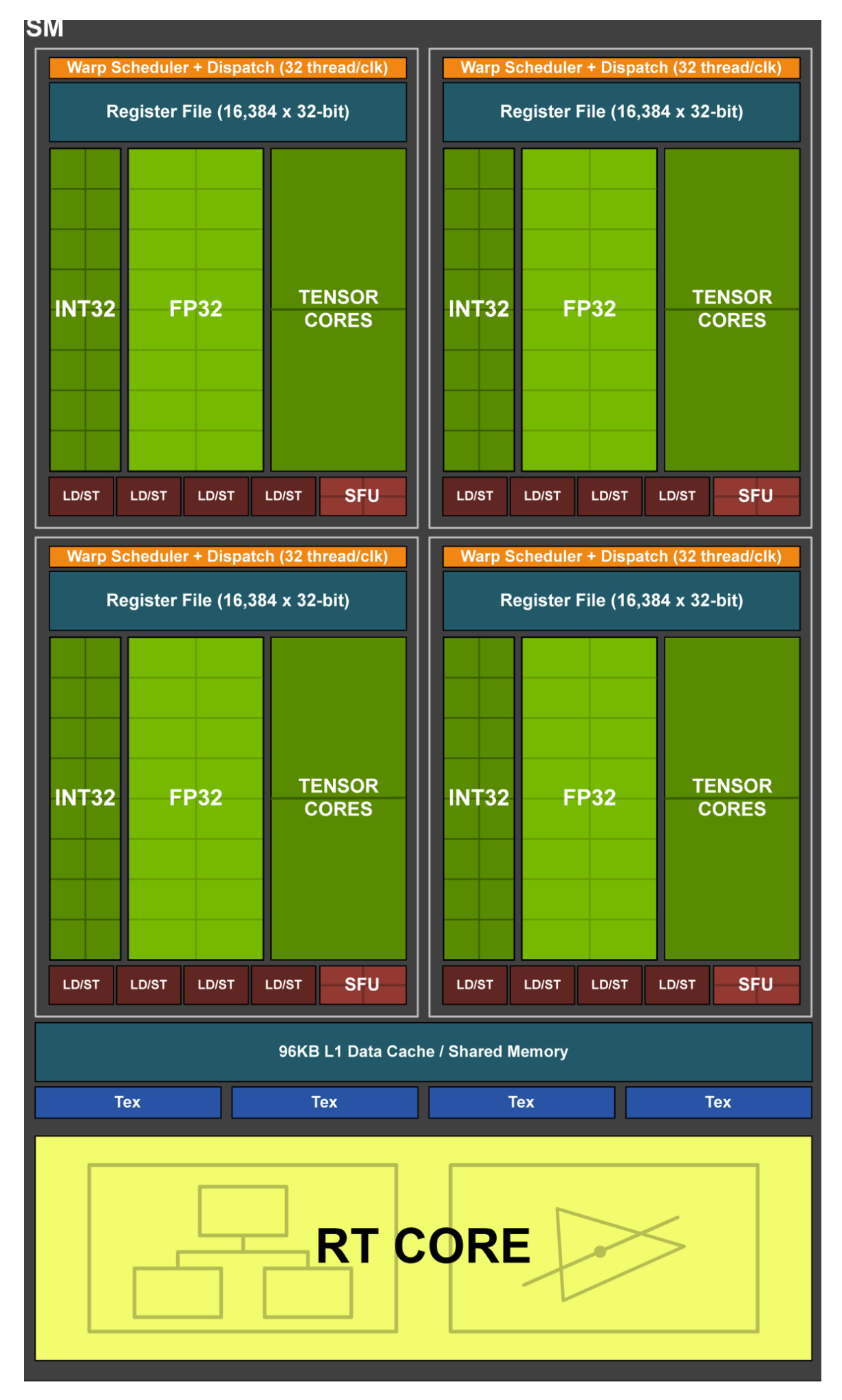
  				上图为turing架构下的SM

假设所有ALU都是无限的, 乘法和加法都只需要1个cycle;那么, 假设cuda core打满和tensor core打满进行计算矩阵乘时:

Cuda core: pascal下, 一个SM有64个thread, 一个线程有4次乘法，5次加法（用half2），粗略估计为8次操作，即8个周期。可以在8个cycle后, 计算出8*8规模的矩阵乘加操作. 其一个cycle可以输出大小为8的有效结果的矩阵.

Tensor Core: 启动4个TC, 每个TC计算结果只需要1 cycle(拉长流水线看), 共需要1个cycle, 计算出8\8规模的矩阵乘加操作, 平均来看, 一个cycle可以输出 8\8 规模的矩阵结果.

综上所述，其加速比: 约等于8. 和官方文档能够对应上.

为什么要引入CuTe?

CuTe, 全称为 "collection of C++ CUDA template abstractions for defining and operating on hierarchically multidimensional layouts of threads and data", 是一个处理嵌套layout的模板抽象的集合, 其并不支持提供现成算子支持, 而是给出耳目一新的数据结构,使得复杂的线性代数计算得以加速.

解决了什么问题? 代价是什么?

解决的问题

主要是解决了之前的二维/N维的tensor中,我们存取数据和做thread对应的时候, 从来都是按照row/col这样线性遍历的; 而引入的新的layout表达, 带来了嵌套的表达关系; 把一块tensor抽象为一个data, 进一步地提升了表达能力; TODO: 但是其所能带来的收益目前还不明朗,;

代价

首先很明显, 是带来了计算偏移量的复杂程度, 其次是代码的可维可测不好做, 毕竟要先脑内转换一遍, 不如单调的直观.

核心: layout计算和表示

[!引用] 这里的理解基于论文和知乎, 链接见下
论文: https://dl.acm.org/doi/pdf/10.1145/3582016.3582018
cute之layout: https://zhuanlan.zhihu.com/p/661182311

核心理解: layout 无非是int -> int 的一个映射, 一种函数罢了.
其具体的表达式如下:

\[F([(a,b),(c,d)]) = [c,d](*)[d_2, d_4] * (s_1 * s_3)+ [a,b] (*)[d_1, d_3] \]

其中, 我们定义一系列表达如下:

\[[(a,b), (c,d)] : 为嵌套下的坐标表示 \]

\[[(s_1, s_2),(s_3, s_4)]:[(d_1,d_2),(d_3,d_4)]: 为layout表示 \]

下面举个例子方便表达:
fig1
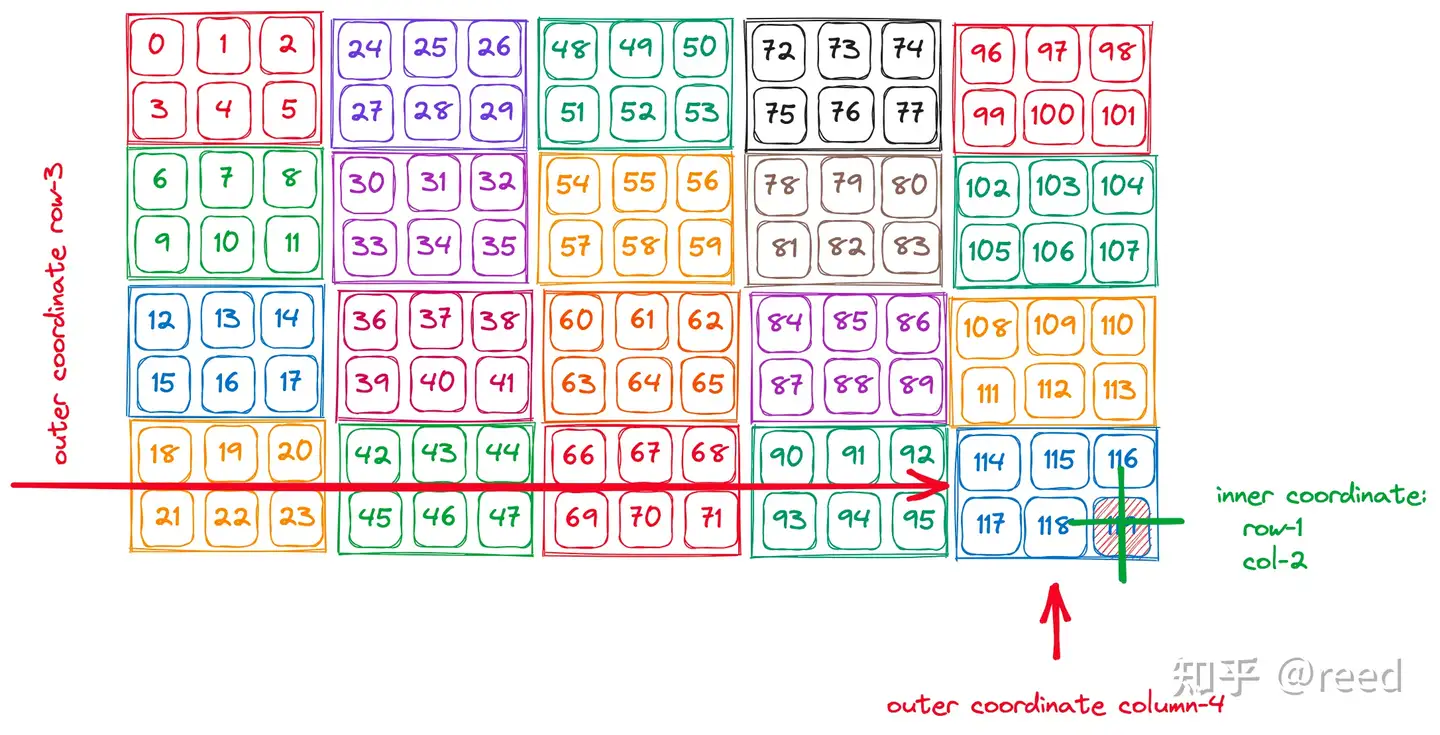
如上图所示, 这个layout可以表示为:

\[[(2,4),(3,5)]:[(3,1),(1,4)] \]

阅读方式是冒号前是shape矩阵,冒号后是stride矩阵. 然后, 阅读方式是: (innner_row, outter_row), (inner_col, outter_col). (innner_stride_row, outtter_stride_row),(innner_stride_col, outter_stride_col);
然后根据上面的计算公式: 假设目前给一个坐标[(1,3),(2,4)], 那么计算出来结果应该是:

\[(3*1 + 4*4) * (2 *3) + (1 * 3 + 2 * 1) = 19 * 6 + 5 =114 + 5 = 119 \]

正好是最后一个thread对应的data. 于是, 截止目前我们可以理解了layout 是如何放置data, 且如何转为一维的index 进行对应.

代数运算: layout的乘除和复合函数

乘法的理解

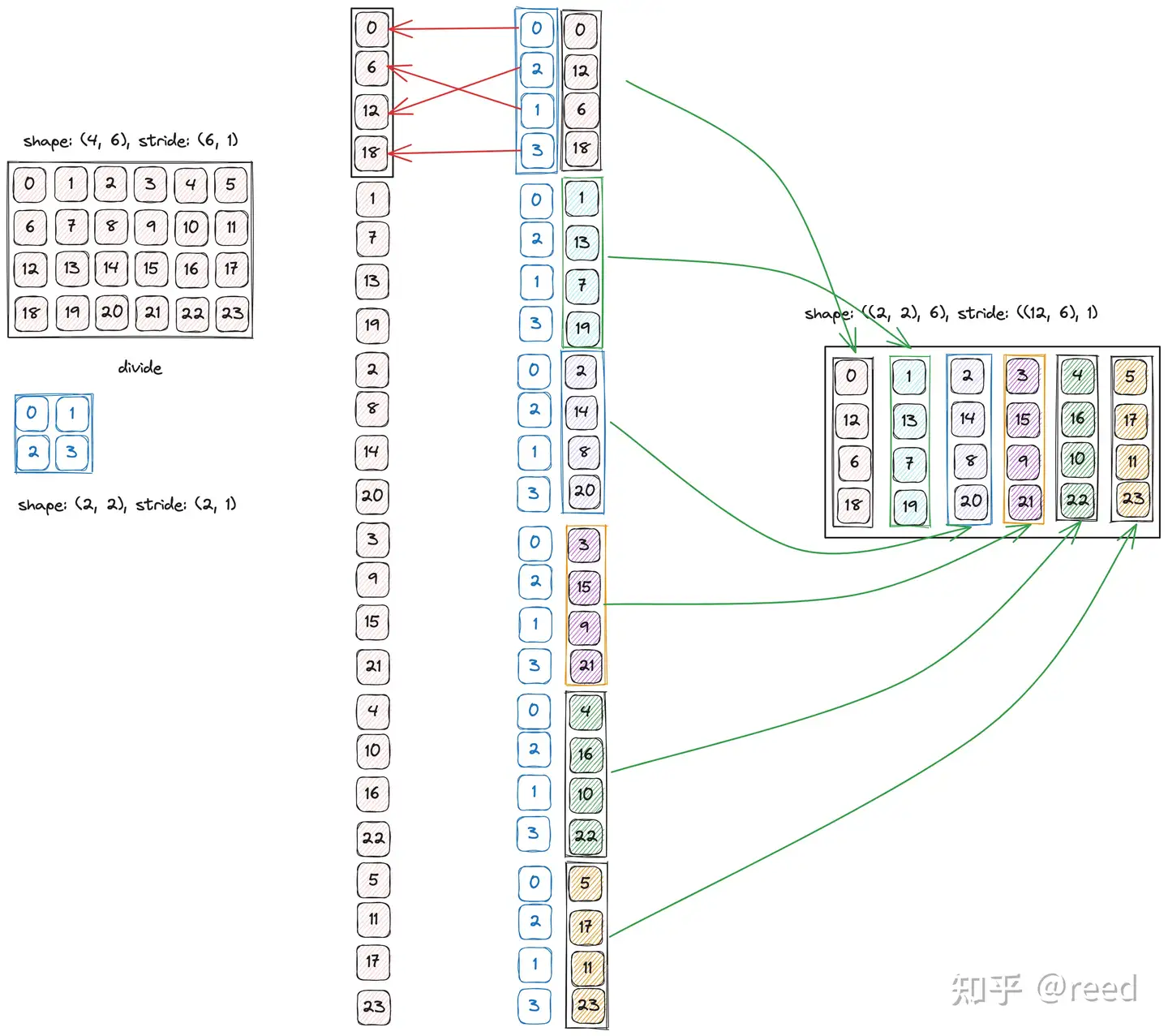
乘法, 这里理解为两个非嵌套的layout进行相乘操作, 那么自然地, 可以将其设置为(a,b)的形式. 其中, a和b都是一个简单的layout. 具体计算如下: 先把b看做一个数,然后按照a的layout填满; 然后把内层layout的数据按照列优先转成一个vector; 之后再对外层layout做同样的操作, 按照列优先转换为一个vector. 具体的示意图可如下所示:

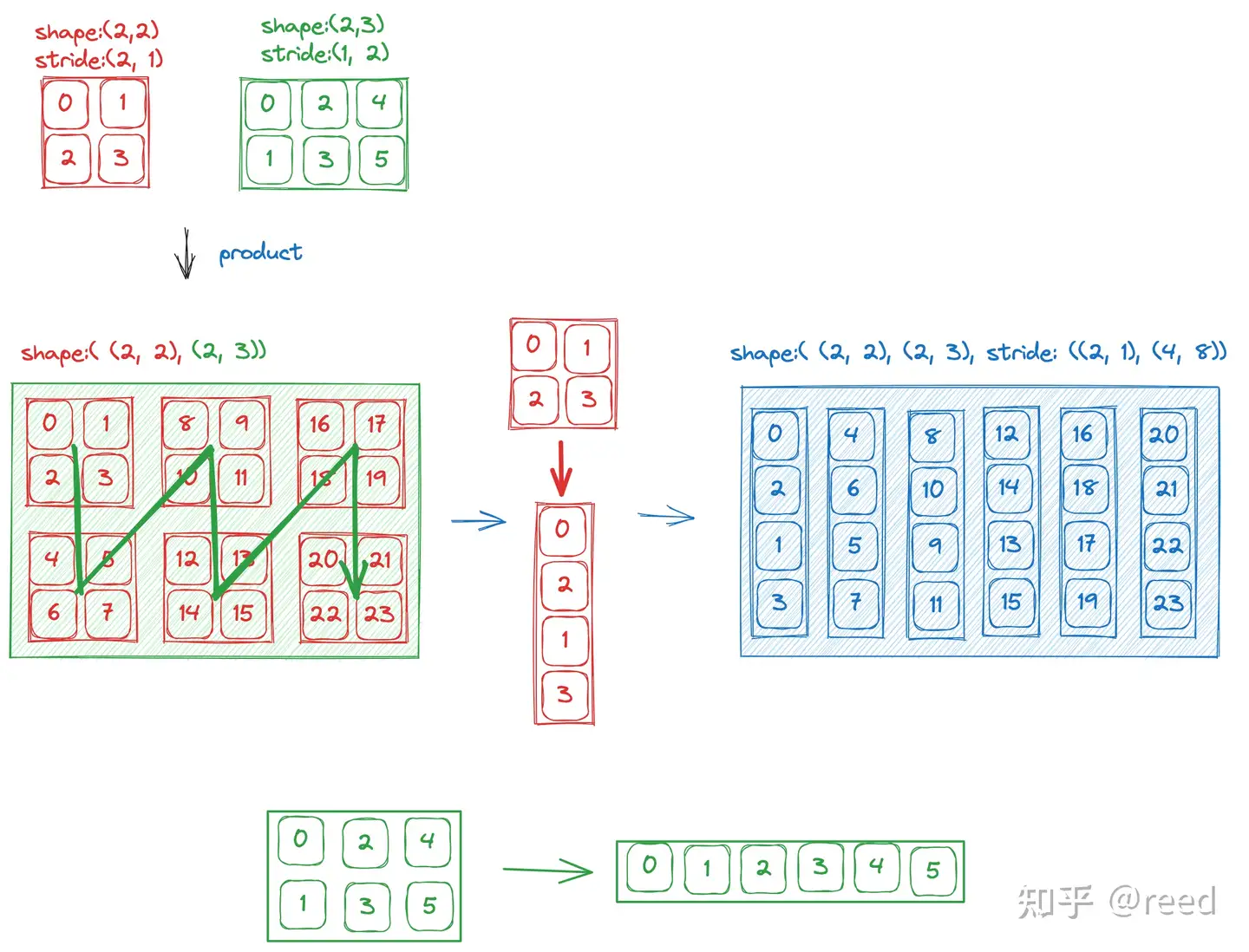
除法的理解

除法, 是乘法的逆运算; 这里定义为a按照b的排列方式,能够排列多少次;即最后的结果应该是(b,size(a) / size(b)). 具体的计算流程如下: 首先, 把b的layout按照列优先,转化为一维表示,; 然后, 把 a的layout 按照列优先展开; 然后对每一个长度为size(b)的a中的一段数据, 按照b的layout的索引, 重新排列一遍数据. 最后, 把重排后的数据依次放入. 实例如下:
fig3

复合函数的理解

复合函数很好理解, 就是先把A的x映射到y, 然后再把y 作为x 传给B函数;
这里x是threadid, 如果id为6, 那么在A中, 映射到6; 然后把6 再作为id传入B, 那么B中对应的是18.
复合函数的示例如下:

代码操作: tensor抽象层

概念理解

这里的tensor 包含两个部分: 分别是前文提到多次的layout 和 engine; 分别代表了抽象的布局和实际的数据存储指针. 在CuTe中, 我们说的tensor 并不等于torch等常见的tensor术语; CuTe中更侧重于数据的摆放和布局描述; 而 torch 中的tensor更多的指代数据本身.

demo代码演示

// z = ax + by + c
template <int kNumElemPerThread = 8>
__global__ void vector_add_local_tile_multi_elem_per_thread_half(
    half *z, int num, const half *x, const half *y, const half a, const half b, const half c) {
  using namespace cute;

  int idx = threadIdx.x + blockIdx.x * blockDim.x;
  if (idx >= num / kNumElemPerThread) { // 未处理非对齐问题
    return;
  }

  Tensor tz = make_tensor(make_gmem_ptr(z), make_shape(num));
  Tensor tx = make_tensor(make_gmem_ptr(x), make_shape(num));
  Tensor ty = make_tensor(make_gmem_ptr(y), make_shape(num));

  Tensor tzr = local_tile(tz, make_shape(Int<kNumElemPerThread>{}), make_coord(idx));
  Tensor txr = local_tile(tx, make_shape(Int<kNumElemPerThread>{}), make_coord(idx));
  Tensor tyr = local_tile(ty, make_shape(Int<kNumElemPerThread>{}), make_coord(idx));

  Tensor txR = make_tensor_like(txr);
  Tensor tyR = make_tensor_like(tyr);
  Tensor tzR = make_tensor_like(tzr);

  // LDG.128
  copy(txr, txR);
  copy(tyr, tyR);

  half2 a2 = {a, a};
  half2 b2 = {b, b};
  half2 c2 = {c, c};

  auto tzR2 = recast<half2>(tzR);
  auto txR2 = recast<half2>(txR);
  auto tyR2 = recast<half2>(tyR);

#pragma unroll
  for (int i = 0; i < size(tzR2); ++i) {
    // two hfma2 instruction
    tzR2(i) = txR2(i) * a2 + (tyR2(i) * b2 + c2);
  }

  auto tzRx = recast<half>(tzR2);

  // STG.128
  copy(tzRx, tzr);
}

代码解读, 从头到尾中值得注意的点:

定义了每个线程负责的数据量为8
在global mem中定义了三个tensor
对gmem中的tensor做切片操作, 这里由于是1维数据, 比较好理解, local_tile函数, 对原tensor做了分割, 按大小为8进行分割, 然后每个thread去取对应的chunk.
下面声明这一段数据在寄存器上放置, 把这一段数据copy到寄存器里;
下面的half2是cuda上常用的优化方式, 这样可以一次性计算两个half数据, 然后也可以利用HFMA指令, 避免额外的指令开销.
计算完后, 把寄存器中的值复制回gmem中.

数据搬运: copy的实现

为什么要设计一个`ldmatrix`指令?

我们都知道, 在设计指令时, 肯定是遵循'奥卡姆剃刀'原则. 但是这里为了加速矩阵的计算, 重新封装了一条指令, 显然是有自己的考量. 我们第一小节的背景补充中已经提到了tensor core 在面对长流水时, 可以接近一个cycle计算出一个小矩阵的乘加结果(HMMA), 那么我们如果想尽可能地"喂饱"这个计算单元, 那么访存压力就会很大, 并且, 要尽可能地把访存指令压缩到一个封装起来的指令, 减少调度的压力, 在所有指令队列中, 尽可能地提升计算指令的百分比. 基于此, 我们下面就来设计一下访存的指令.

`per_warp` 还是 `per_thr` ?

在SIMT下, 寄存器是每个thread私有的, 存放了该thread需要的数据, 但是在tensor core 下, 寄存器是归一个warp私有, 统一进行数据的管理.

举例分析

如下面图示, 如果想load 4个8*8的矩阵数据到寄存器上, 在gpu上, 需要四条LDS.32指令, 每一条指令加载一个8*8大小的矩阵到寄存器上. 而在引入了ldmatrix原语后, 就可以一条指令, 指挥warp把所有数据load到寄存器上.
至于为什么要分开放置, 是因为nv的底层mma ptx 中的矩阵乘指令就是这么映射寄存器的; 具体有什么考量, 笔者认为主要是避开smem和寄存器冲突, 具体深入的讨论链接如下:https://forums.developer.nvidia.com/t/about-register-bank-conflict/47853/2

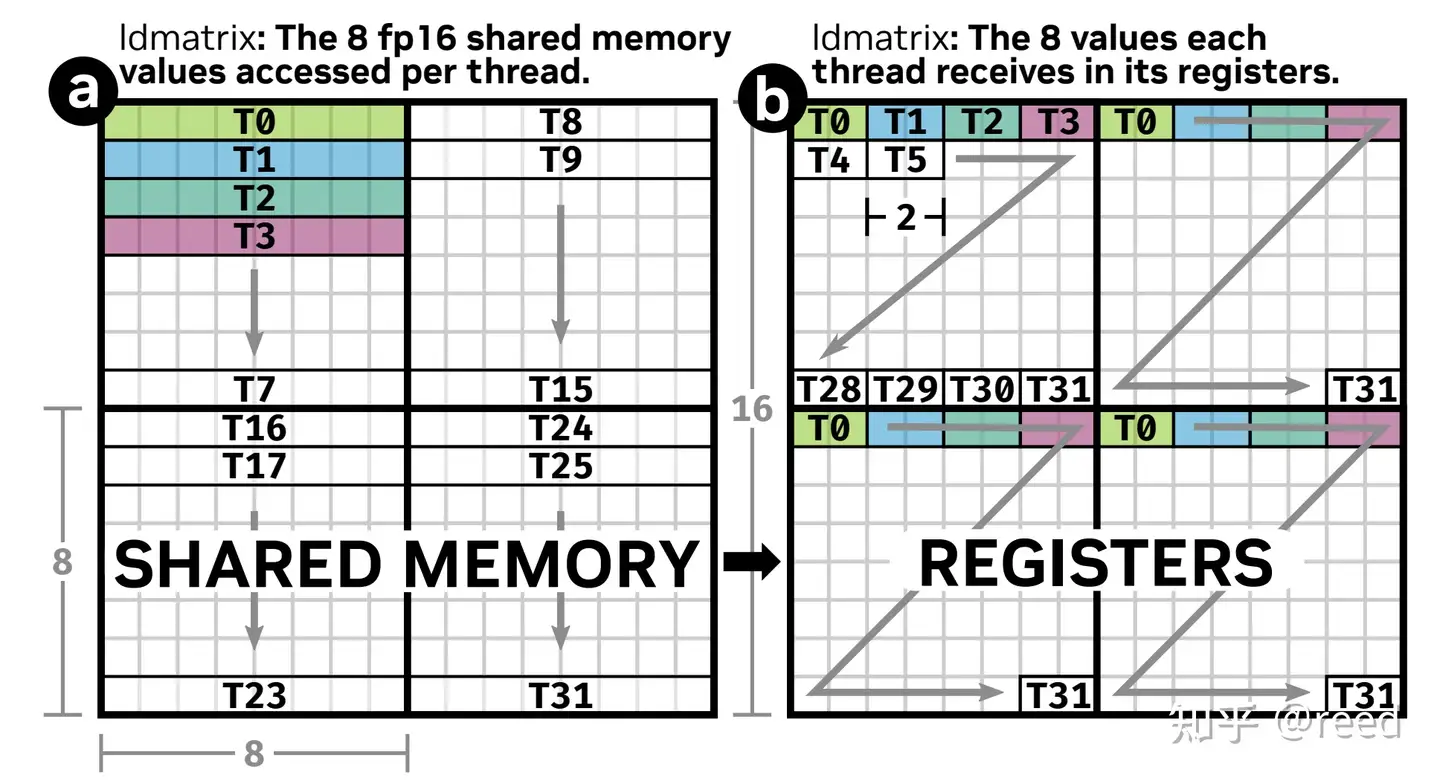
根据上面链接中的github文档和论文链接, 我们可以得知在GPU上, register层面仍然存在bank这一概念; 导致最好交错放置数据, 避免冲突. 演示的例子如下: 如果没有交错放置, 会导致黑框所在部分的寄存器存在冲突, 每次冲突会导致一个cycle的停顿.

大展拳脚: MMA实现

引用链接

本文所采用的代码实现来自于链接:https://zhuanlan.zhihu.com/p/667521327, 该链接详细讲述了实验的效果和为什么这么设置. 在这里本文只引用代码, 用于加深对于cute的理解. 无关部分本文暂不涉及.

simple gemm

template <typename T, int kTileM, int kTileN, int kTileK, typename TiledMMA>
__global__ void gemm_simple(T *Cptr, const T *Aptr, const T *Bptr, int m, int n, int k) {
  Tensor A = make_tensor(make_gmem_ptr(Aptr), make_shape(m, k), make_stride(k, Int<1>{}));
  Tensor B = make_tensor(make_gmem_ptr(Bptr), make_shape(n, k), make_stride(k, Int<1>{}));
  Tensor C = make_tensor(make_gmem_ptr(Cptr), make_shape(m, n), make_stride(n, Int<1>{}));

  int ix = blockIdx.x;
  int iy = blockIdx.y;

  Tensor gA = local_tile(A, make_tile(Int<kTileM>{}, Int<kTileK>{}), make_coord(iy, _));
  Tensor gB = local_tile(B, make_tile(Int<kTileN>{}, Int<kTileK>{}), make_coord(ix, _));
  Tensor gC = local_tile(C, make_tile(Int<kTileM>{}, Int<kTileN>{}), make_coord(iy, ix));
  //  gA(kTileM, kTileK, num_tile_k)
  //  gB(kTileN, kTileK, num_tile_k)
  //  gC(kTileM, kTileN) 

  TiledMMA tiled_mma;
  auto thr_mma = tiled_mma.get_slice(threadIdx.x);
  auto tAgA = thr_mma.partition_A(gA);  // (MMA, MMA_M, MMA_K, num_tile_k)
  auto tBgB = thr_mma.partition_B(gB);  // (MMA, MMA_N, MMA_K, num_tile_k)
  auto tCgC = thr_mma.partition_C(gC);  // (MMA, MMA_M, MMA_N)

  auto tArA = thr_mma.partition_fragment_A(gA(_, _, 0));  // (MMA, MMA_M, MMA_K)
  auto tBrB = thr_mma.partition_fragment_B(gB(_, _, 0));  // (MMA, MMA_N, MMA_K)
  auto tCrC = thr_mma.partition_fragment_C(gC(_, _));     // (MMA, MMA_M, MMA_N)
 
  clear(tCrC);
  
  int num_tile_k = size<2>(gA);
#pragma unroll 1
  for(int itile = 0; itile < num_tile_k; ++itle) {
    cute::copy(tAgA(_, _, _, itile), tArA);
    cute::copy(tBgB(_, _, _, itile), tBrB);

    cute::gemm(tiled_mma, tCrC, tArA, tBrB, tCrC);
  }

  cute::copy(tCrC, tCgC); 
}

int main() {
  ...
  using mma_op = SM80_16x8x16_F16F16F16F16_TN;
  using mma_traits = MMA_Traits<mma_op>;
  using mma_atom = MMA_Atom<mma_traits>;

  auto MMA = decltype(make_tiled_mma(mma_atom{}, 
                      make_layout(Shape<_2, _2, _1>{}), 
                      make_layout(Shape<_1, _2, _1>{})));
  dim3 block(size(MMA{}));
  dim3 grid(n / kTileN, m / kTileM);
  gemm_simple<T, kTileM, kTileN, kTileK, MMA>(Cptr, Aptr, Bptr, m, n, k);
  ...
}

代码简单解读:
以上的代码主要干了这些事情:

告诉编译器, 我要使用的mma的类型是SM80_16x8x16_F16F16F16F16_TN
通过一系列接口, 拿到了最小计算op mma_atom
然后把这个atom操作做了一个拓展, 分别在M方向重复2次, N方向重复两次; 每个线程处理的数据量上, M方向不变, N方向重复两次. 这样, 依次MMA, 就能处理32*32*16这个规模的矩阵乘了.
然后根据超参kTileM, kTileN, kTileK定下grid的大小.
进入kernel, 先定义在gmem上的tensor类型, 然后紧接着根据tile大小进行拆分, 在然后, 对拆分后的tensor, 在线程级别进行拆分;
然后在k方向滑行, 一次次地做gemm操作, 把结果累加到tCrC.
计算完毕后, 把这一块数据load回gdram中.

总结: 灵魂三问, 是什么, 为什么, 要怎么做

CuTe是什么?

我想, 看完了上述的所有讨论,猜测和回答, 读者应当大致了解了CuTe是个什么东西, 本质上就是定义了一套新的tensor表达, 然后基于此, 和tensorcore进行配合, 完成cutlass的使命-----更快速地计算矩阵乘加操作.

为什么要这么做?

在本文最后, 我想我们可以做出如下总结:

适应tensor core 离谱的计算能力, 把优化做到极致, 例如swizzle优化, 就需要前面扭曲的layout排布来优化数据和thread的映射关系, 从而尽可能地提升L2的利用率.
同样地, 为了适应TC的计算能力, 需要把数据的load/store尽可能地优化成一条指令, 于是在copy接口下使用了MMA PTX的ldmatrix指令进行配合.
为了给上层用户降低心智负担, 于是把IR的表达包装成tensor, 暴露给使用者进行任意地拆分,组合,计算.
于是, 这一套基于TC, 以喂饱TC为主旨的逻辑跑通, 就有了cute和cutlass

要怎么做?

NV的cutlass 已经做出了示例, 如何将TC的算力发挥到极致, 里面的优化手段都是可供学习的资料
不要被抽象的表达吓到, 这里也体现了CS的"金科玉律": 当你发现一个feature不够用/不够完成目标时, 在它上面再加一层. 初见不好懂的layout表达, 也只是tensor套tensor.

posted @ 2024-08-19 20:57 Edwardlyz 阅读(132) 评论(1) 编辑收藏举报

刷新页面返回顶部

Edwardlyz