Leetcode: Sqrt(x)

Implement int sqrt(int x).

难度：76，用二分查找。要求是知道结果的范围，取定左界和右界，然后每次砍掉不满足条件的一半，知道左界和右界相遇。算法的时间复杂度是O(logx)，空间复杂度是O(1)。

public class Solution {
    public int sqrt(int x) {
        if (x < 0) {
            return -1;
        }
        if (x == 0) {
            return 0;
        }
        int l = 1;
        int r = x/2 + 1;
        while (l <= r) {
            int m = (l + r)/2;
            if (m <= x/m && x/(m+1) < m+1) return m;
            else if (m > x/m) {
                r = m - 1;
            }
            else {
                l = m + 1;
            }
        }
        return -1;
    }
}

 其实这道题还是很tricky的，上面这行代码13行这么做，而不写成m*m <= x 其实是有深意的，是为了防止m*m的溢出。但是有人会攻击说m <= x/m && x/(m+1) < m+1是不是 m*m <= x && (m+1)*(m+1) > x的等价有效替换呢？ 这个有待商榷。

而且因为用除来解决overflow的问题，新的问题便被引入，那就是denominator为0的问题。为此，x=0的情况要单独考虑（否则m=0会在被除数位置）。左边界设置为1，右边界设置为x/2+1(向上取整以确保l, r之间包含target，否则比如x=1, l=1, r=0; x=2, l=1, r=1; 这些都漏掉了)

因此下面这个做法还是使用乘法，但是为了防止溢出，使用了Longlong型, 它的返回条件如第8行所示，并没有采取我做的方式即 m*m<= x && (m+1)*(m+1)>x , 它这样做是利用到了左右两个边界相遇之后左边界会停在比target大的整数处，而右边界会停在比target小的整数处 

public class Solution {
    int sqrt(int x) {
        int i = 0;
        int j = x / 2 + 1;
        while (i <= j)
        {
            int mid = (i + j) / 2;
            long sq = (long)mid * mid;
            if (sq == x) return mid;
            else if (sq < x) i = mid + 1;
            else j = mid - 1;
        }
        return j;
    }
}

 

2. 牛顿迭代法

另外，有牛顿法的解法，参见http://www.cnblogs.com/AnnieKim/archive/2013/04/18/3028607.html，牛顿法同时也可以解结果是double的情况

   为了方便理解，就先以本题为例：

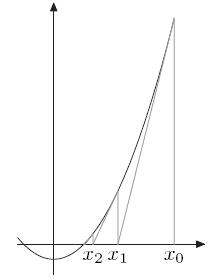
   计算x² = n的解，令f(x)=x²-n，相当于求解f(x)=0的解，如左图所示。

   首先取x₀，如果x₀不是解，做一个经过(x₀,f(x₀))这个点的切线(tangent line)，与x轴的交点为x₁。

   同样的道理，如果x₁不是解，做一个经过(x₁,f(x₁))这个点的切线，与x轴的交点为x₂。

   以此类推。

   以这样的方式得到的x_i会无限趋近于f(x)=0的解。

   判断x_i是否是f(x)=0的解有两种方法：

   一是直接计算f(x_i)的值判断是否为0，二是判断前后两个解x_i和x_i-1是否无限接近。

 

经过(x_i, f(x_i))这个点的切线方程为f(x) = f(x_i) + f’(x_i)(x - x_i)，其中f'(x)为f(x)的导数，本题中为2x。令切线方程等于0，即可求出x_i+1=x_i - f(x_i) / f'(x_i)。

继续化简，x_i+1=x_i - (x_i² - n) / (2x_i) = x_i - x_i / 2 + n / (2x_i) = x_i / 2 + n / 2x_i = (x_i + n/x_i) / 2。

 

举个例子, 为了求sqrt(n)，就是求：f(x) = x^2 - n当f(x) = 0的解

令y = x^2 - n,

取一点(x1, y1), 其切线方程是y-y1 = 2x1*(x - x1)， where 2x1是（x1,y1）处导数

y - (x1^2 - n) = 2x1*(x - x1)

y = 2x1*x - x1^2 - n

令y取零， 0 = 2x1*x - x1^2 - n

x2 <-------- 解得 x = x1/2 + n/2x1 

有了迭代公式，程序就好写了。

输入输出都是int型：

public class Newton {
    public int sqrt(int x) {
            if (x == 0) return 0;
            double last = 0;
            double res = 1;
            while (res != last)
            {
                last = res;
                res = (res + x / res) / 2;
            }
            return (int)res;
        
    }
    
    public static void main(String[] args){
        Newton newton = new Newton();
        System.out.println(newton.sqrt(20));
    }
}

输入输出都是double型，或者输入int, 输出double：

public class Newton {
    public double sqrt(int x) {
            if (x == 0) return 0;
            double last = 0;
            double res = 1;
            while (res != last)
            {
                last = res;
                res = (res + x / res) / 2;
            }
            return res;
        
    }
    
    public static void main(String[] args){
        Newton newton = new Newton();
        System.out.println(newton.sqrt(3));
    }
}