UVA 10537最小树(逆向+字典序输出)
Sindbad the Sailor sold 66 silver spoons to the Sultan of Samarkand. The selling was quite easy; but delivering was complicated. The items were transported over land, passing through several towns and villages. Each town and village demanded an entry toll. There were no tolls for leaving. The toll for entering a village was simply one item. The toll for entering a town was one piece per 20 items carried. For example, to enter a town carrying 70 items, you had to pay 4 items as toll. The towns and villages were situated strategically between rocks, swamps and rivers, so you could not avoid them.
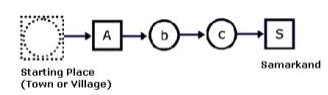
Figure 1: To reach Samarkand with 66 spoons, traveling through a town followed by two villages, you must start with 76 spoons.
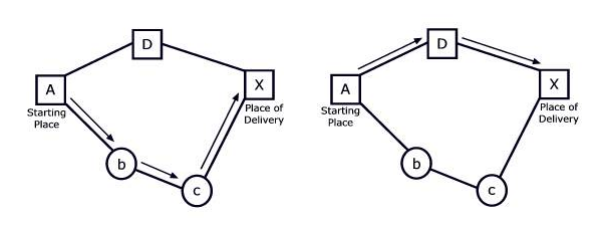
Figure 2: The best route to reach X with 39 spoons, starting from A, is A→b→c→X, shown with arrows in the figure on the left. The best route to reach X with 10 spoons is A→D→X, shown in the figure on the right. The figures display towns as squares and villages as circles.
Predicting the tolls charged in each village or town is quite simple, but finding the best route (the cheapest route) is a real challenge. The best route depends upon the number of items carried. For numbers up to 20, villages and towns charge the same. For large numbers of items, it makes sense to avoid towns and travel through more villages, as illustrated in Figure 2.
You must write a program to solve Sindbads problem. Given the number of items to be delivered to a certain town or village and a road map, your program must determine the total number of items required at the beginning of the journey that uses a cheapest route. You will also have to find the cheapest route. If there is more than one such route, print the lexicographically smallest one (A-n-d is smaller than a-n-d).
Input
The input consists of several test cases. Each test case consists of two parts: the roadmap followed by the delivery details. The first line of the roadmap contains an integer n, which is the number of roads in the map (0 ≤ n). Each of the next n lines contains exactly two letters representing the two endpoints of a road. A capital letter represents a town; a lower case letter represents a village. Roads can be traveled in either direction. Following the roadmap is a single line for the delivery details. This line consists of three things: an integer p (0 < p < 1000000000) for the number of items that must be delivered, a letter for the starting place, and a letter for the place of delivery. The roadmap is always such that the items can be delivered. The last test case is followed by a line containing the number ‘-1’.
Output
The output consists of three lines for each test case. First line displays the case number, second line shows the number of items required at the beginning of the journey and third line shows the path according to the problem statement above. Actually, the path contains all the city/village names that Sindbad sees along his journey. Two consecutive city/village names in the path are separated by a hyphen.
Sample Input
1
a Z
19 a Z
5
A D
D X
A b
b c
c X
39 A X
-1
Sample Output
Case 1:
20
a-Z
Case 2:
44
A-b-c-X
题意:某人带着一批货物从ts出发,如果经过一个村庄(a~z)给1个货物经过一个城市(A~Z)每20个单元给1个货物,比如(21,就需要给2两个货物),给出最后到达集市的货物,求出刚开始出发的所需要的最小货物量
思路:本题本质上就是反向求最小路径问题,d[i]就是每个点所需要的最小货物,想到这一点,就非常好做了,套一下dij的模板就可以了,用priority的话还可以直接就求出最小字典序
但是,我还是犯了四个错误,总结一下,比题目更有用吧
1.const long long inf = 1LL<<60;
2.字典序'a'>'A'
3.因为是从te反向求单源最小路径树,所以最小货物的时候 并不是 y = x+[(x+19)/20],注意,这个y才是我们已知的,所以d[i]应该去求x才对
这里有个公式,比如mod = 20
y = x-[(x+19)/20],已知y求x,则x = y+[(y+18)/19]
4.最后一个锅应该给刘汝佳那本书,好像题目没有说清楚的样子,所以我一开始就以为是终点不收费,起点要收费,而且测试用例也没影响,所以又WA了一次的样子:smile:

#include <iostream> #include <cstdlib> #include <cstdio> #include <cstring> #include <cmath> #include <stack> #include <queue> #include <string> #include <vector> #include <algorithm> const long long inf = 1LL<<60; //long long inf const int MAXN = 60; const int MAXM = 3e4+10; typedef long long ll; struct edge{ int st; int to; //int dist; int next; }; struct heapnode{ int st; ll dist; bool operator < (const heapnode&rhs)const{ /* if(dist!=rhs.dist){ return dist>rhs.dist; }else{ return st>rhs.st; }*/ return dist>rhs.dist; } }; using namespace std; int first[MAXN]; edge e[MAXM]; int top; ll d[MAXN]; int done[MAXN]; int p[MAXN]; int m; ll k; int ts,te; void init(){ top = 0; memset(first,-1,sizeof(first)); } int getnum(char tc){ if(tc<='Z'&&tc>='A')return tc-'A'; return tc-'a'+26; } char rec(int t){ if(t<26) return t+'A'; return t-26+'a'; } void addedege(int u,int v){ e[top].st = u; e[top].to = v; // e[top].dist = dist; e[top].next = first[u]; first[u] = top++; } void dijkstra(int s){ priority_queue<heapnode>Q; memset(done,0,sizeof(done)); for(int i=0;i<MAXN;i++){ d[i] = inf; } d[s] = k; p[s] = -1; while(!Q.empty()){ Q.pop(); } heapnode tmp,tf; tmp.dist = 0LL; tmp.st = s; Q.push(tmp); int u; ll tt; while(!Q.empty()){ tf = Q.top(); Q.pop(); u = tf.st; if(u==ts) break; if(done[u])continue; done[u] = 1; for(int i=first[u];i!=-1;i=e[i].next){ if(u<26){ //tt = (d[e[i].st])/19+!!((d[e[i].st])%19); tt = (ll)(d[e[i].st]+18LL)/19LL; }else{ tt = 1LL; } if(d[e[i].to]>d[e[i].st]+tt){ d[e[i].to] = d[e[i].st] + tt; tmp.st = e[i].to; tmp.dist = d[e[i].to]; Q.push(tmp); p[e[i].to] = e[i].st; }else if(d[e[i].to]==d[e[i].st]+tt){ p[e[i].to] = min(p[e[i].to],e[i].st); } } } } void print(int u){ if(p[u]==-1){ printf("%c\n",rec(u)); return; } printf("%c-",rec(u)); print(p[u]); } int main() { char st1[10],st2[10]; int u,v; int tc=0; while(scanf("%d",&m)!=EOF&&m!=-1){ init(); for(int i=0;i<m;i++){ scanf("%s%s",st1,st2); u = getnum(st1[0]); v = getnum(st2[0]); addedege(u,v); addedege(v,u); } scanf("%lld%s%s",&k,st1,st2); ts = getnum(st1[0]); te = getnum(st2[0]); dijkstra(te); printf("Case %d:\n",++tc); printf("%lld\n",d[ts]); print(ts); } return 0; }

/* 0 2 A A 6 a c c e e d a b b f f d 19 a d 25 A B B C C D D E E F F G G H H I I J J K K L L M M N N O O P P Q Q R R S S T T U U V V W W X X Y Y Z 999999999 A Z 4 A b A B b c B c 18 A c 4 A b A B b c B c 19 A c 5 A D D X A b b c c X 39 A X */

/* Case 1: 2 A Case 2: 22 a-b-f-d Case 3: 3605038190 A-B-C-D-E-F-G-H-I-J-K-L-M-N-O-P-Q-R-S-T-U-V-W-X-Y-Z Case 4: 20 A-B-c Case 5: 21 A-b-c Case 6: 44 A-b-c-X */



 浙公网安备 33010602011771号
浙公网安备 33010602011771号